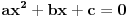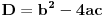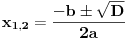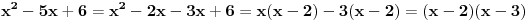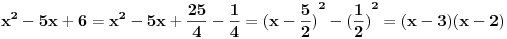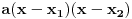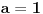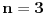[ Castodian42 @ 22.02.2008. 20:42 ] @
| Treba mi mala pomoc. Odrediti nula funkcije: 1.) y=x-1/x+1 2.) y=2x-1/x*+1 3.) y=x*-5x+6/x*-1 * je kvadrat jer ne mogu naci kvadraturu na tastaturi ne mogu provaliti kako se resavaju ovakvi zadaci, jedan detaljno uradjen bi mi mnogo znacio, ne mogu zid probiti glavom kolko god udaro pa upomoc! Ne znam uopste kako resiti ni jednacinu 0=x-1/x+1 nista mi nije jasno :( |