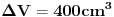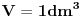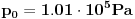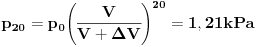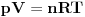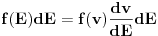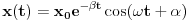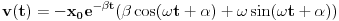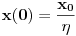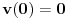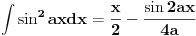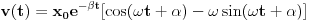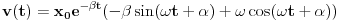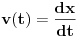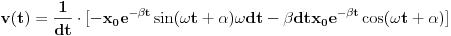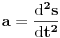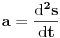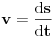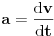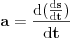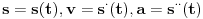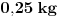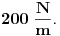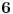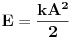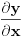[ R A V E N @ 25.02.2008. 18:32 ] @
|
[ Boba90 @ 26.02.2008. 14:28 ] @
hmm da bi zadatak imao smisla trebalo bi da stoji ... ispumpavanje balona zapremine V u rezervoar...
onda bi trebao da prines Bojlov zakon za svaki korak... [ Bata1981 @ 26.02.2008. 18:28 ] @
Predpostavljam da je po=101000[Pa] atmosferski pritisak,ali ipak da pitam za svaki slucaj da li je to manometarski ili apsolutni pritisam?
Citat: Boba90: hmm da bi zadatak imao smisla trebalo bi da stoji ... ispumpavanje balona zapremine V u rezervoar... onda bi trebao da prines Bojlov zakon za svaki korak... Zasto tako mislis? Pod tih 400[cm^3] podrazumevas radnu zapreminu pumpe? [ Boba90 @ 26.02.2008. 20:08 ] @
pa zato sto se rezervoar pominje tek na kraju a da pre nije receno gde se vazduh uduvava ;)
[ R A V E N @ 28.02.2008. 04:44 ] @
Citat: Bata1981: Predpostavljam da je po=101000[Pa] atmosferski pritisak Pa...rezervoari su obično zatvoreni,bez kontakta sa okolinom,tako da je to unutrašnji pritisak,bez pridodatog atmosferskog pritiska,odnosno "manometarski",ako si na to mislio. Zadatak sam tačno naveo kako piše u knjizi. Citat: Boba90: hmm da bi zadatak imao smisla trebalo bi da stoji ... ispumpavanje balona zapremine V u rezervoar... onda bi trebao da prines Bojlov zakon za svaki korak... Kako? [Ovu poruku je menjao R A V E N dana 28.02.2008. u 06:25 GMT+1] [ Bata1981 @ 28.02.2008. 10:36 ] @
RAVEN ja predpostavljam da u rezervoaru vlada atmosferski pritisak pa.
p-apsolutni pritisak. pa-atmosferski pritisak. pm-manometarski pritisak. p=pa+pm. To je ono sto sam hteo da pitam,nije bila velika mudrost.Kada stignem da ga uradim okacicu ga ovde,nije tezak. Pozdrav. [ R A V E N @ 29.02.2008. 09:10 ] @
Na to sam upravo i mislio.
Stvar je u tome da,kad se pominje "rezervoar",zapravo se misli na taj balon zapremine  ,ne postoji vanjski rezervoar u koji se gas prebacuje pumpom. ,ne postoji vanjski rezervoar u koji se gas prebacuje pumpom.Ma da,zadatak treba raditi preko Boyle-Mariotteovog zakona,što se i vidi iz transformacije 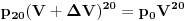 - dok pumpa usisava gas,zapremine - dok pumpa usisava gas,zapremine  i i 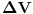 sačinjavaju jedan entitet. sačinjavaju jedan entitet.Samo je problem što sad intuitivno osjećam da je izraz koji sam postavio gore rješenje,a ne mogu da ga izvedem "na papiru". [Ovu poruku je menjao R A V E N dana 29.02.2008. u 10:23 GMT+1] [ tomkeus @ 29.02.2008. 14:30 ] @
Zapremina rezervoara je
 . Na početku je gas na pritisku . Na početku je gas na pritisku 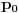 . Kada se klip podigne zapremina se uvećava na . Kada se klip podigne zapremina se uvećava na 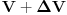 a pritisak se smanjuje na a pritisak se smanjuje na 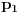 . Pošto je proces izotermski važi . Pošto je proces izotermski važi 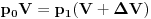 . Potom se cilindar klipa odvoji od rezervoara i klip se spušta pri čemu sada istiska gas u spoljašnju sredinu preko nekog ventila. Dakle pritisak u rezervoaru je smanjen na . Potom se cilindar klipa odvoji od rezervoara i klip se spušta pri čemu sada istiska gas u spoljašnju sredinu preko nekog ventila. Dakle pritisak u rezervoaru je smanjen na 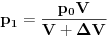 . Cilindar se ponovo spaja sa rezervoarom i ciklus počinje iz početka i kada se završi u rezervoaru vlada pritisak . Cilindar se ponovo spaja sa rezervoarom i ciklus počinje iz početka i kada se završi u rezervoaru vlada pritisak 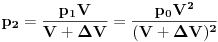 . Ovi ciklusi se ponavljaju ukupno 20 puta, tako da ćemo po očiglednoj šemi dobiti da je posle 20-tog ciklusa pritisak . Ovi ciklusi se ponavljaju ukupno 20 puta, tako da ćemo po očiglednoj šemi dobiti da je posle 20-tog ciklusa pritisak 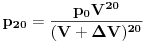 . .[ R A V E N @ 29.02.2008. 21:42 ] @
Da,to je ono što je trebalo,hvala,tomkeus!
[ R A V E N @ 15.03.2008. 18:32 ] @
A postavljen je ovakav problem:
Izvesti izraz za funkciju raspodjele molekula po energijama ako je raspodjela molekula po brzinama Maxwellova. Naravno,ovo se odnosi na neki gas. Evo kako sam ja uradio - krenuo sam od Maxwellove funkcije raspodjele molekula po brzinama: 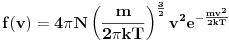 te sam u gornjem izrazu,u stepenu broja  , izvršio zamjenu , izvršio zamjenu 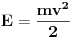 ,pomnožio desnu stranu gornjeg izraza sa ,pomnožio desnu stranu gornjeg izraza sa 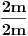 ,pa sam i tada mogao izvršiti zamjenu ,pa sam i tada mogao izvršiti zamjenu 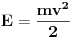 ,te sam dobio izraz: ,te sam dobio izraz: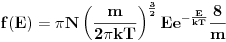 Da li je ovaj izraz tačan,ako nije,zašto nije i kako treba pravilno postupiti?U jednoj knjizi sam našao jedan izraz koji ima veze sa ovim 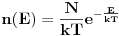 ,ali mislim da on zapravo daje broj molekula sa energijom ,ali mislim da on zapravo daje broj molekula sa energijom  . .[Ovu poruku je menjao R A V E N dana 15.03.2008. u 20:29 GMT+1] [ tomkeus @ 15.03.2008. 19:48 ] @
[ R A V E N @ 15.03.2008. 21:36 ] @
Ne razumijem.
[ tomkeus @ 15.03.2008. 21:57 ] @
Verovatnoća da čestica ima brzinu
 u intervalu u intervalu 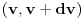 je data sa je data sa 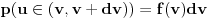 gde je gde je 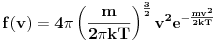 . Raspodela se, dakle, koristi u tom kontekstu. Kada tražimo raspodelu po energijama, nama treba takva funkcija raspodele koja nam daje verovatnoću da čestica ima energiju . Raspodela se, dakle, koristi u tom kontekstu. Kada tražimo raspodelu po energijama, nama treba takva funkcija raspodele koja nam daje verovatnoću da čestica ima energiju 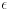 u intervalu u intervalu 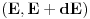 na sledeći način na sledeći način 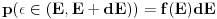 . Stoga, ne samo što moraš da napraviš smenu u . Stoga, ne samo što moraš da napraviš smenu u 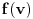 , moraš da napraviš smenu , moraš da napraviš smenu 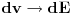 što rezultuje jakobijanom jer što rezultuje jakobijanom jer 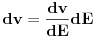 . .[ R A V E N @ 02.04.2008. 20:56 ] @
Izgleda neki more advanced dio diferencijalnog računa.Možda ću se pozabaviti time kasnije.
U međuvremenu je dat ovaj zadatak: Neka malo tijelo vrši prigušeno oscilovanje sa kružnom učestanošću 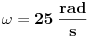 .Naći koeficijent prigušenja .Naći koeficijent prigušenja  ,ako u početnom trenutku brzina tijela iznosi ,ako u početnom trenutku brzina tijela iznosi 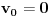 ,a njegovo pomjeranje od položaja ravnoteže je ,a njegovo pomjeranje od položaja ravnoteže je 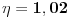 puta manje od amplitude u početnom trenutku. puta manje od amplitude u početnom trenutku.Rješenje: 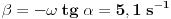 [Ovu poruku je menjao R A V E N dana 02.04.2008. u 22:13 GMT+1] [ R A V E N @ 06.04.2008. 14:31 ] @
Bilo ko?Ja sam već iscrpio sve mogućnosti.Tim više je zbunjujuće što se koristi neki ugao u rješenju za kojeg ja iz daleka ne vidim kako bi se mogao inkorporirati.Jedina formula s kojom raspolažem je
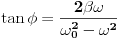 ali ona pokriva oblast prinudnih oscilacija,gdje je  -razlika faza prinudne sile i oscilatora na kojeg ona djeluje -razlika faza prinudne sile i oscilatora na kojeg ona djeluje -koeficijent prigušenja -koeficijent prigušenja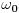 -početna kružna brzina oscilovanja. -početna kružna brzina oscilovanja.[Ovu poruku je menjao R A V E N dana 06.04.2008. u 16:07 GMT+1] [ tomkeus @ 06.04.2008. 15:05 ] @
[ R A V E N @ 06.04.2008. 16:55 ] @
Hvala.
 Nisam raspolagao s takvom formulom za brzinu.Zbilja ogroman je gap između teoretskih temelja i primjene te teorije na rješavanje problema. Nisam raspolagao s takvom formulom za brzinu.Zbilja ogroman je gap između teoretskih temelja i primjene te teorije na rješavanje problema.A imam i ovu nejasnoću:recimo da imamo šipku na čijem jednom kraju je dat talas koji se širi prema drugom kraju te šipke koji je učvršćen,dakle nepomičan je.Na tom kraju će doći pored refleksije talasa i do refleksije dilatacije.Dok će talas promijeniti svoj predznak,dilatacija neće,jer naime piše u knjizi(Mladen Paić - Gibanja,Sile,Valovi,Školska Knjiga,Zagreb,1994.,strana 422.,1. - 5. red odozgo): "Dilatacije se međutim reflektiraju bez promjene predznaka.Imamo,naime,za upadni val 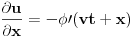 a za reflektirani val 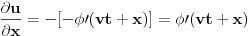 " " Kako da se reflektiraju bez promjene predznaka,kad su izrazi na desnoj strani obje gornje jednačine sa različitim predznacima?Možda je stvar u ovome Kako da se reflektiraju bez promjene predznaka,kad su izrazi na desnoj strani obje gornje jednačine sa različitim predznacima?Možda je stvar u ovome  što mi je nepoznat dio matematičkog aparata(mada je problem u tome što formalno očekuju od nas da poznajemo nešto što se radi tek na drugoj godini - ovdje konkretno iz diferencijanih jednačina - iz matematike dok radimo fiziku sa prve godine). što mi je nepoznat dio matematičkog aparata(mada je problem u tome što formalno očekuju od nas da poznajemo nešto što se radi tek na drugoj godini - ovdje konkretno iz diferencijanih jednačina - iz matematike dok radimo fiziku sa prve godine). - otklon čestica šipke pod utjecajem talasa - otklon čestica šipke pod utjecajem talasa - mjesto na kojem se posmatra otkon - mjesto na kojem se posmatra otkon[Ovu poruku je menjao R A V E N dana 06.04.2008. u 18:28 GMT+1] [ tomkeus @ 06.04.2008. 18:15 ] @
Citat: R A V E N: Hvala.  Nisam raspolagao s takvom formulom za brzinu.Zbilja ogroman je gap između teoretskih temelja i primjene te teorije na rješavanje problema. Nisam raspolagao s takvom formulom za brzinu.Zbilja ogroman je gap između teoretskih temelja i primjene te teorije na rješavanje problema.??? Ako raspolažeš formulom za položaj raspolažeš formulom za brzinu zato što je druga običan izvod prve. A formulu za položaj bi morao da znaš ako si ikada prošao pored zgrade u kojoj se predaje fizika, a uostalom, ona je rešenje jednačine kretanja prigušenog LHO-a 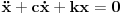 . .Citat: R A V E N "Dilatacije se međutim reflektiraju bez promjene predznaka.Imamo,naime,za upadni val 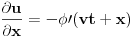 a za reflektirani val 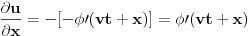 " " Kako da se reflektiraju bez promjene predznaka,kad su izrazi na desnoj strani obje gornje jednačine sa različitim predznacima?Možda je stvar u ovome Kako da se reflektiraju bez promjene predznaka,kad su izrazi na desnoj strani obje gornje jednačine sa različitim predznacima?Možda je stvar u ovome 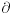 što mi je nepoznat dio matematičkog aparata(mada je problem u tome što formalno očekuju od nas da poznajemo nešto što se radi tek na drugoj godini - ovdje konkretno iz diferencijanih jednačina - iz matematike dok radimo fiziku sa prve godine). što mi je nepoznat dio matematičkog aparata(mada je problem u tome što formalno očekuju od nas da poznajemo nešto što se radi tek na drugoj godini - ovdje konkretno iz diferencijanih jednačina - iz matematike dok radimo fiziku sa prve godine).[Ovu poruku je menjao R A V E N dana 06.04.2008. u 18:28 GMT+1] 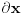 je u principu diferencijal*, pa ako se upadni talas prostire u smeru porasta x koordinate je u principu diferencijal*, pa ako se upadni talas prostire u smeru porasta x koordinate 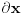 će biti pozitivan dok će za odbijeni talas biti negativan jer se ovaj prostire u smeru opadanja x koordinate. Zbog ovoga jednačine zapravo imaju isti predznak zato što se upadni i reflektovani talas se prostiru u suprotnim smerovima tako da će za njih izvodi po koordinati će biti pozitivan dok će za odbijeni talas biti negativan jer se ovaj prostire u smeru opadanja x koordinate. Zbog ovoga jednačine zapravo imaju isti predznak zato što se upadni i reflektovani talas se prostiru u suprotnim smerovima tako da će za njih izvodi po koordinati 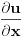 imati suprotne znakove. imati suprotne znakove. edit: *Zapravo, setio sam se boljeg izraza: priraštaj koordinate. [Ovu poruku je menjao tomkeus dana 06.04.2008. u 19:50 GMT+1] [ R A V E N @ 11.04.2008. 21:49 ] @
"Ako si ikada prošao pored zgrade u kojoj se predaje fizika,treba da znaš ovo."
Ma ako je tako,kampovaću pored zgrade. Ali stvarno,poznat mi je sad taj princip rezonovanja iz kinematike 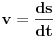 i i 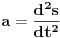 ,samo što je to kod nas prezentirano na fakultetu "na suho",mehanički i formalno,bez pravog poimanja suštine procesa,pa se i ne poveže u neku globalniju sliku.Sve se svodi na beskonačnu i zamornu prepisanciju teorije i zadataka s table.Meni je,na primjer,potpuno nejasna ta notacija ,samo što je to kod nas prezentirano na fakultetu "na suho",mehanički i formalno,bez pravog poimanja suštine procesa,pa se i ne poveže u neku globalniju sliku.Sve se svodi na beskonačnu i zamornu prepisanciju teorije i zadataka s table.Meni je,na primjer,potpuno nejasna ta notacija 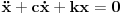 ,mada znam da je nešto oko diferenijalnih jednačina,za koje se očekuje da ih studenti ravno poznaju kada dođu iz srednje. ,mada znam da je nešto oko diferenijalnih jednačina,za koje se očekuje da ih studenti ravno poznaju kada dođu iz srednje.Premalo se oslanja na literaturu,i takva je praksa možda na cijelom Balkanu,knjige se smatraju nepotrebnima,mada nisu nepodnošljivo skupe.Meni je,naprimjer,puno ugodnije nešto samostalno "prokljuviti" i naučiti nego biti "samljeven" tempom na fakultetu(moj je elektrotehnički). Mislim da bi jedna knjiga koja bi u blažoj formi objasnila diferencijalni i integralni račun primjenjen na tretiranje fizikalnih problema bila veoma korisna studentima,makar napravila samo privremeni odmak od strogosti matematičkog tretiranja i protumačila stvari laičkim jezikom. [Ovu poruku je menjao R A V E N dana 11.04.2008. u 23:34 GMT+1] [ R A V E N @ 11.04.2008. 22:07 ] @
Jedno pitanje:da li je Youngov modul elastičnosti kod čvrstih tijela formalno analogan pritisku kod gasova?
[ Boba90 @ 12.04.2008. 15:02 ] @
nije. analogan je prozizvodu pritiska gasa i Poasaonovog koeficijenta gama koji predstavlja odnos specificnih toplota pri const. p i V
[ R A V E N @ 12.04.2008. 18:52 ] @
Ali i taj
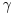 je bezdimenzionalni broj,te da li možemo zaključiti da,dok pritisak predstavlja silu po jedinici površine koja se opire zgušnjavanju gasa dok se neki talas prenosi kroz njega,dotle Youngov mogul elastičnosti također predstavlja silu po jedinici površine koja se opire dilataciji čestica čvrstog tijela dok se neki talas širi kroz njega? je bezdimenzionalni broj,te da li možemo zaključiti da,dok pritisak predstavlja silu po jedinici površine koja se opire zgušnjavanju gasa dok se neki talas prenosi kroz njega,dotle Youngov mogul elastičnosti također predstavlja silu po jedinici površine koja se opire dilataciji čestica čvrstog tijela dok se neki talas širi kroz njega?Razlog zašto ovo pitam je što bih htio probati izvesti relaciju za raspored energije talasa u čvrstom tijelu polazeći od relacije koja je osnov za izvođenje relacije rasporeda energije talasa u gasovima,a u kojoj konfigurira pritisak. [ R A V E N @ 12.04.2008. 19:13 ] @
Recimo da je zadat naizmjenični napon funkcijom
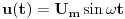 .Potrebno je pronaći njegovu efektivnu vrijednost. .Potrebno je pronaći njegovu efektivnu vrijednost.Koristeći formulu 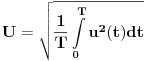 (u koju uvrstim smjenu (u koju uvrstim smjenu 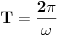 ) i koristeći slijedeću formulu za rješavanje integrala ) i koristeći slijedeću formulu za rješavanje integrala 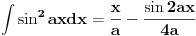 ja pišem: ja pišem: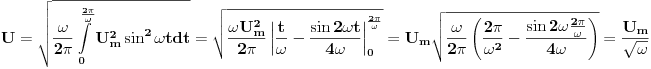 mada je tačan rezultat 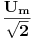 U čemu je greška? Možda u tome što je napon uzet bez njegove početne faze? [Ovu poruku je menjao R A V E N dana 13.04.2008. u 01:26 GMT+1] [ R A V E N @ 13.04.2008. 00:52 ] @
[ zzzz @ 14.04.2008. 13:08 ] @
Citat: R A V E N: Ali stvarno,poznat mi je sad taj princip rezonovanja iz kinematike 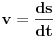 i i 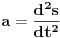 ,samo što je to kod nas prezentirano na fakultetu "na suho",mehanički i formalno,bez pravog poimanja suštine procesa,pa se i ne poveže u neku globalniju sliku.Sve se svodi na beskonačnu i zamornu prepisanciju teorije i zadataka s table.Meni je,na primjer,potpuno nejasna ta notacija ,samo što je to kod nas prezentirano na fakultetu "na suho",mehanički i formalno,bez pravog poimanja suštine procesa,pa se i ne poveže u neku globalniju sliku.Sve se svodi na beskonačnu i zamornu prepisanciju teorije i zadataka s table.Meni je,na primjer,potpuno nejasna ta notacija 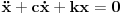 ,mada znam da je nešto oko diferenijalnih jednačina,za koje se očekuje da ih studenti ravno poznaju kada dođu iz srednje. ,mada znam da je nešto oko diferenijalnih jednačina,za koje se očekuje da ih studenti ravno poznaju kada dođu iz srednje.Ako je baš takav taj predavač onda on nema pojma. Trebalo je nacrtati idealizirani fizikalni model.Materijalna tačka (m) vezana za oprugu oscilira oko neke srednje tačke (x=0).Pri tom sila trenja prigušuje (koči) oscilacije. Na to tijelo u opštem položaju djeluju tri sile i one su u dinamičkoj ravnoteži : -Sila opruge koja je proporcionalna izduženju ili skraćenju opruge.. F(o)= c*x -Inercijalna sila koja je jednaka umnošku mase i ubrzanja... F(i)= m*a -Sita trenja koja je proporcionalno brzini kretanja...... F(t)= k*v Ravnoteža: F(0)+F(i)+F(t)=0 (c je konstantna opruge, a k je koeficijent trenja) Prvi izvod puta po vremenu je brzina v, a drugi izvod je ubrzanje a. U onoj formuli je još uzeto i da je masa m=1 sa ciljem da što više zamaskira realnost i zbuni.A trenje je odabrano kao da je proporcionalno brzini kretanja iz istih razloga, iako svako zna da to nije tako.Cilj je bio i da se napravi što ljepša diferencijalna jednačina najjednostavnijeg oscilatornog modela, zaboravi na realnu stvarnost, i uolovi u vode matematike. A suština je :Imamo dva akumulatora (spremnika) energije.Opruga akumulira potencijalnu energiju elastičnom deformacijom, a tijelo kinetičku kretanjem.Pri prelasku energije iz jednog u drugi spremnik zbog trenja nastaju gubici.Da bi to nekako zapisali matematički moramo što više idealizirati fizikalne pojmove... [ R A V E N @ 14.04.2008. 20:01 ] @
Citat: Ako je baš takav taj predavač onda on nema pojma. U čemu tačno? [ Boba90 @ 14.04.2008. 22:46 ] @
[ R A V E N @ 17.04.2008. 05:40 ] @
[ Boba90 @ 17.04.2008. 12:51 ] @
[ R A V E N @ 18.04.2008. 17:10 ] @
[ R A V E N @ 18.04.2008. 17:37 ] @
Zamislimo neku granu u električnom kolu naizmjenične struje gdje su serijski vezani otpornik
 i zavojnica reaktivne otpornosti i zavojnica reaktivne otpornosti 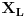 .Kompleksna impedansa takve grane će iznositi .Kompleksna impedansa takve grane će iznositi 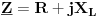 .Ako sada želimo izračunati kompleksnu admitansu .Ako sada želimo izračunati kompleksnu admitansu 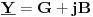 (kompleksnu prividnu provodnost,gdje je (kompleksnu prividnu provodnost,gdje je  aktivna provodnost aktivna provodnost  reaktivna provodnost ili susceptansa)te grane,pišemo: reaktivna provodnost ili susceptansa)te grane,pišemo: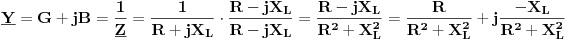 Pri čemu ispada da je 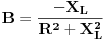 ,mada se u zadacima koristi ,mada se u zadacima koristi 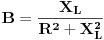 ,a što se i intuitivno dobiva kao tačno,jer susceptansa ne može biti negativna. ,a što se i intuitivno dobiva kao tačno,jer susceptansa ne može biti negativna.Moje pitanje glasi:Zašto se minus tek tako odbacuje,ima li neko dublje fizikalno objašnjenje toga ili je i ovdje samo riječ o primjeni rigoroznih matematičkih pristupa na nesavršeni realni svijet?Ako sam u pravu,minus se može odbaciti jer je skup kompleksnih brojeva samo,uslovno rečeno,"umjetno" proširenje skupa realnih brojeva. [Ovu poruku je menjao R A V E N dana 18.04.2008. u 18:50 GMT+1] [ R A V E N @ 06.05.2008. 07:55 ] @
Slična pojava se pojavljuje kod proračuna aktivne i reaktivne snage grane koja sadrži otpornk i zavojnicu,naime ispred rezultata dolazi "-".
Ako je potrebno da izložim primjer? [Ovu poruku je menjao R A V E N dana 06.05.2008. u 19:15 GMT+1] [ R A V E N @ 06.05.2008. 22:08 ] @
Možda je objašnjenje u tome da dok jedan parametar raste(susceptansa
 ),drugi pada(induktivna reaktansa ),drugi pada(induktivna reaktansa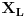 ),kao kod Faradayevog zakona elektromagnetne indukcije: ),kao kod Faradayevog zakona elektromagnetne indukcije: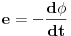 Magnetno polje koje je uzrokovano indukovanom strujom,a koja je opet uzrokovana indukovanom elektromotornom silom  ,je svojim smjerom u suprotnosti sa promjenom vanjskog fluksa ,je svojim smjerom u suprotnosti sa promjenom vanjskog fluksa  koji uzrokuje tu elektromotornu silu. koji uzrokuje tu elektromotornu silu.Ali šta ako je kondenzator umjesto zavojnice?Tada nema minusa. [Ovu poruku je menjao R A V E N dana 06.05.2008. u 23:18 GMT+1] [ R A V E N @ 06.05.2008. 22:33 ] @
Imam još jedno teoretsko pitanje:
zašto se pri proračunu ukupne snage 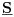 potrošača u kolu naizmjenične struje koristi konjugovano-kompleksna vrijednost struje potrošača u kolu naizmjenične struje koristi konjugovano-kompleksna vrijednost struje 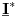 umjesto prave vrijednosti umjesto prave vrijednosti 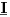 odnosno zašto formula 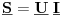 ne daje pravu sliku kompleksne snage potrošača nego to daje formula ne daje pravu sliku kompleksne snage potrošača nego to daje formula 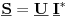 ? ?[Ovu poruku je menjao R A V E N dana 07.05.2008. u 03:02 GMT+1] [ R A V E N @ 28.10.2008. 10:03 ] @
Code: Problem 9: Nasuprot homogenom štapu mase  na liniji koja prolazi okomito na štap kroz njegov centar nalazi se tijelo mase na liniji koja prolazi okomito na štap kroz njegov centar nalazi se tijelo mase  udaljeno za dužinu od udaljeno za dužinu od 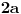 od štapa.Dužina štapa je također od štapa.Dužina štapa je također 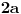 .Pronaći gravitacionu silu kojom štap djeluje na tijelo. .Pronaći gravitacionu silu kojom štap djeluje na tijelo.Evo kako sam ja radio: Slika:  Djelić mase štapa 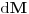 djeluje na tijelo silom djeluje na tijelo silom 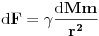 . .Pošto se komponenta sile 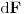 u smjeru u smjeru  -ose kompenzira sa komponentom istog intenziteta,ali suprotnog smijera,koja potječe od osnosimetričnog djelića mase -ose kompenzira sa komponentom istog intenziteta,ali suprotnog smijera,koja potječe od osnosimetričnog djelića mase 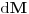 ,postoji samo komponenta sile u smjeru ,postoji samo komponenta sile u smjeru  -ose, -ose,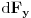 . .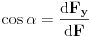 ; ; 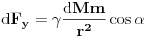 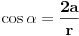 ; ; 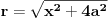 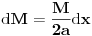 ; ; 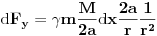 ; ; 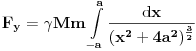 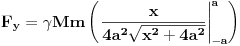 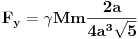 ; ; 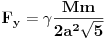 no međutim tačan rezultat je 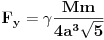 ,šta više u knjizi je dato ,šta više u knjizi je dato 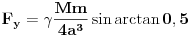 ,ali je ,ali je 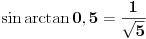 . .Vjerovatno je pravilno to da treba sve promjenljive svesti na diferencijal ugla,ali me interesuje zašto ovaj moj postupak nije valjan?Nešto je tu do geometrije... [Ovu poruku je menjao R A V E N dana 29.10.2008. u 15:13 GMT+1] [ tomkeus @ 29.10.2008. 03:55 ] @
Nisam gledao baš detaljno, ali čini mi se da si dobro uradio. Ono što bez detaljnog gledanja mogu da vidim je da rezultat u knjizi dimenziono ne valja jer je obrnuto proporcionalan kubu dužine.
[ R A V E N @ 29.10.2008. 10:18 ] @
Zapravo je moja greška u tome gdje sam naveo rezultat iz knjige.Ispravno je
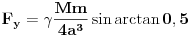 što je meni bizaran rezultat,jer nemam ideje kako su ga dobili,ali to mi i nije toliko bitno ovdje.To i ne mijenja ništa jer je rezultat još uvijek dimenziono neispravan. Ispravio sam i gore. [Ovu poruku je menjao R A V E N dana 29.10.2008. u 11:32 GMT+1] [ tomkeus @ 29.10.2008. 13:44 ] @
Ko god da je pisao rezultat u knjizi bio je lenj zato što je
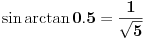 . Rezultat u knjizi se razlikuje od tvog samo zbog toga što je u njemu . Rezultat u knjizi se razlikuje od tvog samo zbog toga što je u njemu 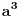 što je neispravno. Dobro si uradio zadatak. što je neispravno. Dobro si uradio zadatak.edit: Tek sada sam video da si već napisao u prethodnom postu 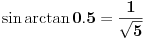 . .[Ovu poruku je menjao tomkeus dana 29.10.2008. u 16:31 GMT+1] [ R A V E N @ 17.11.2008. 23:00 ] @
Hvala,tomkeus,kasnije ću se vratiti tom problemu,jer imam još jedan način rješavanja na umu.Samo da rezimiramo:tačan rezultat
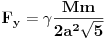 se dobije kada se netačan se dobije kada se netačan 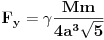 podijeli sa podijeli sa 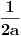 ? ?Code: Problem: 10 Imamo dvije kugle.Masa prve je 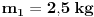 a njena brzina a njena brzina 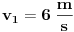 .Masa druge je .Masa druge je 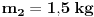 i njena brzina je i njena brzina je 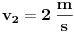 .Kugle se kreću jedna prema drugoj i između njih se odigra centralni idealno neelastični sudar.Kolika je brzina kugli poslije sudara? .Kugle se kreću jedna prema drugoj i između njih se odigra centralni idealno neelastični sudar.Kolika je brzina kugli poslije sudara?S obzirom na to da je riječ o centralnom idealno neelastičnom sudaru,kugle će nakon sudara formirati jedinstveno tijelo mase 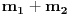 brzine brzine  .Koristeći zakon o održanju količine kretanja,imamo: .Koristeći zakon o održanju količine kretanja,imamo: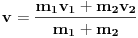 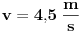 no međutim knjiga daje 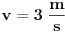 .Jesam li ja propustio šta ovdje? .Jesam li ja propustio šta ovdje?[Ovu poruku je menjao R A V E N dana 18.11.2008. u 00:19 GMT+1] [ zzzz @ 18.11.2008. 00:10 ] @
Kugle se kreću jedna prema drugoj
Da pogriješio si.Brzine imaju suprotne predznake, pa je u brojniku 12 kgm/s , a ne 18. I još treba reći da je dobijeni rezultat 3 m/s u smjeru v1, a ne bilo kamo. [ R A V E N @ 29.12.2008. 13:39 ] @
Code: Problem 11: U vodi pliva valjak tako da je 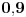 dijelova njegove visine pod vodom.Na vodu se naspe sloj ulja tako da potpuno prekrije valjak.Koji dio visine valjka će se nalaziti pod vodom nakon sipanja ulja?Gustina vode: dijelova njegove visine pod vodom.Na vodu se naspe sloj ulja tako da potpuno prekrije valjak.Koji dio visine valjka će se nalaziti pod vodom nakon sipanja ulja?Gustina vode: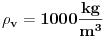 ,a gustina ulja: ,a gustina ulja: 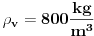 . .Izrada: Prije dodavanja ulja,pritisak kojim voda djeluje na donju osnovu valjka i pritisak kojim valjak djeluje na vodu ispod njega su u ravnoteži. Taj pritisak iznosi: 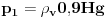 . .Nakon dodavanja ulja,pritisak na tom mjestu poraste,poraste sila uzgona u smjeru ka gore i valjak se penje do tačke kada će ponovo pritisci biti u ravnoteži.Sada će na donju osnovu valjka djelovati pritisak,gdje je 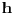 visina za koju se pomjerio valjak: visina za koju se pomjerio valjak: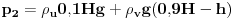 Imamo: 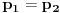 iz čega možemo dobiti da je: 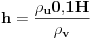 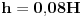 prema tome,naša tražena visina je: 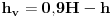 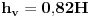 . .Ali tačan odgovor je: 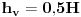 .Gdje sam ja pogriješio? .Gdje sam ja pogriješio?[Ovu poruku je menjao R A V E N dana 29.12.2008. u 15:30 GMT+1] [ zzzz @ 29.12.2008. 16:59 ] @
Nakon dodavanja ulja,pritisak na tom mjestu poraste,poraste sila uzgona u smjeru ka gore....
Dodavanjem ulja uzgon opada jer je ulje rijeđe od vode, pa valjak pomalo tone u odnosu na novonastali nivo.Sila uzgona jednaka je težini istisnute tekućine. Treba najprije naći gustinu tijela iz uslova jednakosti težine tijela i sile uzgona. 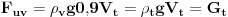 A onda napraviti situsciju gdje je tijelo dijelom pod vodom, a dijelom pod uljem. 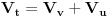 i i 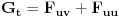 -indeksi su za ulje(u), vodu(v) i tijelo(t) [ R A V E N @ 29.12.2008. 17:52 ] @
Ali ako tone,samo će porasti dio visine valjka koja se nalazi u području pod vodom?
Znači,treba vodu i ulje tretirati kao jedan "fluid"? [Ovu poruku je menjao R A V E N dana 29.12.2008. u 19:25 GMT+1] [ zzzz @ 29.12.2008. 19:53 ] @
R A V E N: Ali ako tone,samo će porasti dio visine valjka koja se nalazi u području pod vodom?
Ne.Dio visine u vodi će se smanjiti.A tone u odnosu na gornji nivo ulja.Ako naspeš ulja samo za 0,1 H valjak će se podići iznad nivoa ali za manje od 0,1 H.Sipamo dalje sve dok taj dio što viri ne bude nula.Kad bi sipali još valjak bi bio potopljen, ali nebi potonuo. Znači,treba vodu i ulje tretirati kao jedan "fluid"? Ne.Sloj ulja pliva na vodi i ako koristiš Arhimedov zakon dobićeš da mu je visina jednaka polovini valjka. Može se to isto dobiti i pomoću statičkih pritisaka na bazu valjka odozdo, ali nije lijepo ignorisati slavnog Arhimeda. [Ovu poruku je menjao zzzz dana 29.12.2008. u 21:04 GMT+1] [ R A V E N @ 08.02.2009. 18:06 ] @
Code: Problem 12: Imamo šuplju kuglu(šupljina je sfernog oblika) unutrašnjeg i vanjskog prečnika 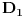 i i 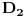 ,respektivno.Ako kugla pliva u tečnosti gustine ,respektivno.Ako kugla pliva u tečnosti gustine 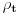 ,dok materijal koji sačinjava njen sferni sloj ima gustinu ,dok materijal koji sačinjava njen sferni sloj ima gustinu 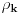 ,koliko mora biti težak teg ,koliko mora biti težak teg  kojeg stavimo u unutrašnjost kugle da bi ona lebdjela u tečnosti? kojeg stavimo u unutrašnjost kugle da bi ona lebdjela u tečnosti?Riješenje: Ako zamislimo da imamo punu kuglu,da bi ona lebdjela u tečnosti mora biti 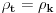 .Prema tome,težina .Prema tome,težina 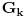 takve kugle mora biti jednaka zbiru težina sfernog sloja i tega i imamo: takve kugle mora biti jednaka zbiru težina sfernog sloja i tega i imamo: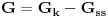 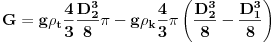 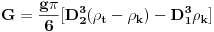 Tačno ili ne? [Ovu poruku je menjao R A V E N dana 08.02.2009. u 19:20 GMT+1] [ R A V E N @ 09.02.2009. 13:24 ] @
Code: Problem 13: Riješio sam još jedan zadatak čiju provjeru trebam: Akvarijum kockastog oblika širine stranice  je do vrha napunjen vodom.Izračunati ukupnu silu koja djeluje na stranice akvarijuma zbog pritiska vode.Na kojoj visini je do vrha napunjen vodom.Izračunati ukupnu silu koja djeluje na stranice akvarijuma zbog pritiska vode.Na kojoj visini 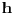 od dna akvarijuma se nalazi napadna tačka te sile? od dna akvarijuma se nalazi napadna tačka te sile?Riješenje: Na segment površine stranice 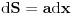 djeluje pritisak djeluje pritisak 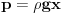 .Prema tome je .Prema tome je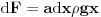 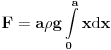 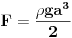 što je ukupna sila na jednu stranu,samo pomnožimo sa  da dobijemo ukupnu silu. da dobijemo ukupnu silu.Što se tiče napadne tačke,jasno je da vrijedi 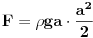 iz čega vidimo da sila odgovara hidrostatičkom pritisku da dnu akvarijuma,pa je napadna tačka na iz čega vidimo da sila odgovara hidrostatičkom pritisku da dnu akvarijuma,pa je napadna tačka na 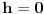 . .[Ovu poruku je menjao R A V E N dana 09.02.2009. u 14:45 GMT+1] [ zzzz @ 09.02.2009. 19:25 ] @
Na kojoj visini od dna akvarijuma se nalazi napadna tačka te sile?
Ovo nije dobro rješeno.Treba to uraditi pomoću izjednačavanja momenta rezultante oko neke tačke (naka je to x=0) i momenta svih onih dF. Ispašće x=2/3a tj. h=1/3a. [ R A V E N @ 09.02.2009. 20:55 ] @
Hvala.
Može li neko pogledati i Problem 12? [ R A V E N @ 18.02.2009. 20:18 ] @
[ R A V E N @ 18.02.2009. 22:56 ] @
Code: Problem 14: Imam još jedno,prilično trivijalno pitanje: Osnovna jednačina za talas je 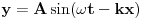 .No u drugoj knjizi nađoh da je ta jednačina .No u drugoj knjizi nađoh da je ta jednačina 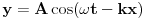 .Ako sam dobro shvatio,ovaj drugi oblik se dobiva iz prvog ako se ishodište koordinatnog sistema pomjeri za dužinu koja odgovara .Ako sam dobro shvatio,ovaj drugi oblik se dobiva iz prvog ako se ishodište koordinatnog sistema pomjeri za dužinu koja odgovara 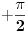 ,dakle udesno?I zašto se koristi ovaj drugi oblik? ,dakle udesno?I zašto se koristi ovaj drugi oblik? je odstupanje posmatrane tačke sredine od njenog stabilnog položaja u trenutku je odstupanje posmatrane tačke sredine od njenog stabilnog položaja u trenutku  ,a na udaljenosti ,a na udaljenosti  od ishodišta koordinatnog sistema. od ishodišta koordinatnog sistema. je amplituda talasa a je amplituda talasa a 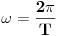 i i 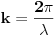 gdje je gdje je  period talasa, a period talasa, a  njegova talasna dužina. njegova talasna dužina.[Ovu poruku je menjao R A V E N dana 19.02.2009. u 00:21 GMT+1] [ zzzz @ 19.02.2009. 00:12 ] @
[ R A V E N @ 12.04.2009. 21:44 ] @
Code: Problem 15: Odrediti izraz za period prigušenog oscilovanja tijela mase  koje visi na opruzi,ako je poznato izduženje opruge koje visi na opruzi,ako je poznato izduženje opruge  pri stanju mirovanja i logaritamski dekrement prigušenja pri stanju mirovanja i logaritamski dekrement prigušenja  . .Riješenje: 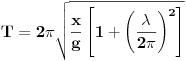 . .Postaviću samo dio svog postupka,da ne duljim nepotrebno: Ako krenem od izraza koji opisuje kružnu frekvenciju kod ovakvog kretanja 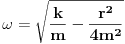 ,od izraza ,od izraza 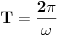 i znajući da je i znajući da je 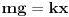 gdje je gdje je  - konstanta opruge - konstanta opruge - koeficijent otpora sredine - koeficijent otpora sredine - zna se šta je - zna se šta jedobivam ovo: 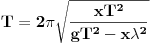 . .Iskoristio sam da je 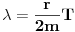 ,ali ne znam više šta da iskoristim. ,ali ne znam više šta da iskoristim.[Ovu poruku je menjao R A V E N dana 12.04.2009. u 23:00 GMT+1] [ Milan Milosevic @ 13.04.2009. 07:12 ] @
 [att_img] [ R A V E N @ 13.04.2009. 09:59 ] @
 [ R A V E N @ 14.04.2009. 22:35 ] @
[ zzzz @ 14.04.2009. 22:55 ] @
Da, A izračunaš baš tako i to je to.A "m" bi moglo poslužiti ako treba uzračunati
frekvenciju oscilovanja kao i maksimalnu brzinu brzinu kugle. [ R A V E N @ 14.04.2009. 23:26 ] @
Jasno je onda.Stvar je u tome što sam ja mislio da je nepisano pravilo da se svaki brojčani podatak mora iskoristiti negdje u procesu dobivanja finalnog rezultata.
[ R A V E N @ 15.04.2009. 13:39 ] @
Code: Problem 17: Ako je sila otpora sredine proporcionalna sa brzinom tijela koje osciluje: a)ni jedna od ostalih tvrdnji nije tačna - TAČNO b)frekvencija opada sa vremenom - NETAČNO,JER FREKVENCIJA UOPŠTE NIJE FUNKCIJA CJELOKUPNOG VREMENA: 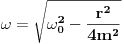 c)pomjeraj tijela je sinusoidalna funkcija vremena - NETAČNO,NEGO JE UGAONOG POMJERAJA d)brzina je sinusoidalna funkcija vremena - NETAČNO,NEGO JE UGAONOG POMJERAJA e)mehanička energija je konstantna - NETAČNO,NEGO TEŽI KA NULI KAKO VRIJEME PROLAZI Trebam provjeru da li sam tačno ovdje zaključivao.Zapravo,ovo je trik-pitanje jer je sila otpora sredine uvijek u ovakvim razmatranjima kvantitativno proporcionalna brzini oscilirajućeg tijela: 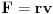 . .[Ovu poruku je menjao R A V E N dana 15.04.2009. u 14:55 GMT+1] [ R A V E N @ 18.04.2009. 23:29 ] @
Eh,evo nas,tema se vrti u krug i došli smo do talasa(mehaničkih).
Code: Problem 18: Kod mehaničkih talasa,kakva je to veličina relativna deformacija sredine? Očigledno je u pitanju bezdimenzionalni broj.  [Ovu poruku je menjao R A V E N dana 19.04.2009. u 00:58 GMT+1] [ R A V E N @ 21.04.2009. 18:16 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|