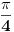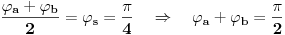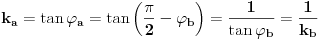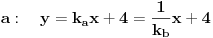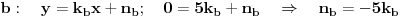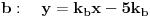[ h4su @ 27.02.2008. 09:01 ] @
Odrediti prave a i b tako da A(0,4) pripada a , B(5,0) pripada b tako da je prava s : 2x-2y-1=0 simetrala ugla koji obrazuju prave a i b. Kroz pravu A može se postaviti normala na s i naći tačka presjeka D.Zatim naći tačku A' tako da je D sredina duži AA' te preko tačkaka B i A' napisati jednačinu prave b.Isti postupak ponoviti i za pravu a.Pitanje je kako se može drugačije to brže rješiti? |