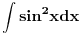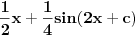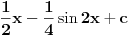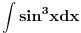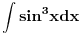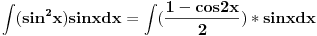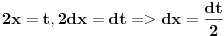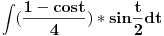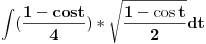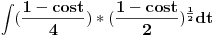Samo primeniš formulu za sinus polovine ugla i dalje se rešava rutinski, takoreći u jednom redu.

Samo, kao rešenje bi trebalo da se dobije .

Nisam znao za ovu formulu... Nisam je nasao ovde: http://www.elitesecurity.org/t264447-0#1599836
Hvala puno...

Btw, ako ti nije tesko, da li bi mogao da mi kazes kako se dolazi do ove formule ili neki link gde postoje ove formule ili da mi ispises formule za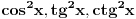

Nadam se da ne smaram puno ;)

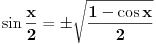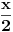Sad sam pogledao, postoji formula na toj temi, ne znam kako je nisi video. Jedino što je tamo napisana u svom "originalnom" obliku, . Ja sam je ovde napisao kvadriranu i umesto sam napisao . Imaš tamo formule i za cos, tg i ctg.

Formulu možeš dobiti tako što pođeš od formule za kosinus dvostrukog ugla: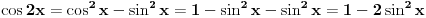

,

odakle je .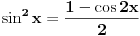

Na sličan način možeš doći i do formule za 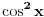, a samim tim i za kvadrat tangensa i kotangensa.

Probaj Arkanto sada da uradis

npr.

bi trebalo onda trebalo da bude:

Smena




AAAA
Kako je tesko kucati u ovom cudu :)
Jesam li bar na dobrom putu ili negde BRUKA gresim posto mi ovo deluje komplikovano....?

Btw, zaboravio sam da kazem...
Hvala puno sto ste odvojili vremena da mi izvedete ove formule, razumeo sam izvodjenje...
Sto se tice ovog sin^3x mislim da nesto ovako "komplikovano" ne bi trebalo da dobijem... Verujem da ce biti sin^2x u sklopu neke druge funkcije, ali da ide na treci stepen, ne verujem... Mada...

Nije BRUKA nego (BRUKA)^2. Salim se:
Mnogo je laksi integral od (sinx)^3 nego onaj sto si vec uradio od (sinx)^2

(sinx)^3 = (sinx)^2 * sinx = (1-(cosx)^2)*sinx i onda uvedes smenu cosx=t......... i postaje integral od -(1 - t^2)*dt =-t + (t^3)/3 + C

Uopstene mnogo je lakse kad su na neparan stepen nego na paran. Recimo:

(sinx)^5=(sinx)^4*sinx = ((sinx)^2)^2*sinx = (1-(cosx)^2)^2 * sinx i onda ista smena cosx=t......... i postaje integral od -((1 - t^2))^2*dt =
integral od -(1 - 2*t^2 + t^4)*dt = -t + 2*(t^3)/3 - (t^5)/5 + C


P.S. integral od (sinx)^2=sinx*sinx moze da se uradi i parcijalnom integracijom bez teske trigonometrije. Ne znam da pisem u ovom cudu. Ako ti treba kako ide napisacu u Word-u pa cu zalepiti sliku.

Medjutim, (sinx)^4 ne moze lako da se uradi parcijalnom integracijom, tako da je, za parne stepene, principski bolji nacin preko formula koje ti je dao Danijel011. Za neparne stepene to ne funkcionise.
Pozdrav




<sub>[Ovu poruku je menjao miki069 dana 10.03.2008. u 23:42 GMT+1]

[Ovu poruku je menjao miki069 dana 10.03.2008. u 23:43 GMT+1]

[Ovu poruku je menjao miki069 dana 10.03.2008. u 23:48 GMT+1]</sub>

Heh... Sta drugo reci? :)
Moracu malo vise da poradim na smeni :)