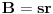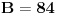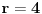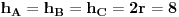[ IBD @ 16.03.2008. 11:53 ] @
| Zdravo ja sam nov ovde i imam problem kod zadatka koji glasi ovako: Osnova piramide je trougao sa stranicama 13cm ,14cm,15cm,sve bocne strane nagnute su prema ravni osnove pod uglom od 60 stepeni izracunati povrsinu Piramide. Iz zadatka provazilaze trvdjena: 1.Sve apoteme su jednake 2.podnozje visine piramide je centar upisanog kruga u bazu iz ovih trdjenja izvukao sam sledece jednakosti: B=21r(gde je r poluprecnik upisanog kruga u bazu a B povrsina baze) M= 21hA=21hB=hC(hA,hB,hC, su apoteme koje odgovaraju redom ivicama baze:a,b,c) r=1/2hA=1/2hB=1/2hC H=r*(kvadratni koren koren iz 3) ne znam kako da napisem Koren iz 3 H je visina piramide P=21(hA+r)=21(hB+r)=21(hC+r) Problem je u tome sto ne znam kako pomocu ovih jednakosti da dodjem do povrsine,probao sam na vise nacina ali ne ide. deluje kao da nema dovljno podataka pa ako mozete da mi pomognete, unapred zahvalan. |