[ Mirage @ 19.03.2008. 17:06 ] @
| imam 2 zadatka: 1. Ispitati da li je dati graf 2-obojiv. 2. Da li dati graf G sadrzi artikulacioni cvor? Ima li neko nesto iz literature sto bi moglo da pomogne ili neke algoritme? Hvala... |
|
[ Mirage @ 19.03.2008. 17:06 ] @
[ amel @ 19.03.2008. 18:43 ] @
Nemam puno vremena ali cu ti pokusati odgovoriti na pitanje broj 1.
Svaki BIpartitni graf je 2-obojiv. Evo uzmimo npr 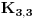 ili uopsteno ili uopsteno 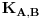 . On izgleda ovako . On izgleda ovako(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6) = P gdje su 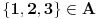 i i 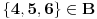 cvorovi a notacija cvorovi a notacija 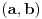 veza izmedju tacaka a i b. veza izmedju tacaka a i b.Algoritam je jednostavan. Provjeravas sve parove. Ako za sve parove iz P postoji jedan par (a, b) gde je 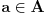 i i 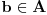 onda graf nije 2-obojiv. Zasto? Evo zasto. Recimo da je u P jedan par (1,2) onda imamo sljedece stanje onda graf nije 2-obojiv. Zasto? Evo zasto. Recimo da je u P jedan par (1,2) onda imamo sljedece stanje(1, 2) (1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6) = P Za prvi par (1, 2) bojimo 1 sa crvenom, 2 sa plavom. (1, 4) 1. ostaje crvena, 4 bojimo sa plavom ... (2, 4) postoji kolizija jer 2 je obojeno sa plavom i 4 obojeno sa plavom, moramo dodati jos jednu farbu sto u ovom slucaju graf nije 2-bojiv. Nadam se da si skontao u cemu je problem. To sam samo naveo za bipartitne grafove, a za ostale nije isto problem skonati mada sad nemam vremena nesto posebno Uzdravlje Amel [ masetrt @ 19.03.2008. 18:55 ] @
Generalno postoji nekoliko algoritama koji se najcesce koriste u prolasku kroz grafove i najprostiji su:
Dijkstra, Breadth-first, Depth-first ostale stvari ces morati uklopis u implementacije tih algoritama Knkretno za tvoje probleme pogledaj linkove http://www.cs.auckland.ac.nz/~ute/220ft/graphalg/graphalg.html http://en.wikipedia.org/wiki/Category:Graph_algorithms Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|