[ petarm @ 27.03.2008. 19:38 ] @
|
[ Vincenity @ 22.06.2008. 15:49 ] @
Baza topologije nije skup podskupova, nego podskup topologije...
Ako je manja baza ona koja ima manje elemenata, bolje je raditi sa manjom... Banach-ov i Hilbert-ov prostor su topoloski po definiciji, znaci samo specijalan slucaj. Cim imas normu imas i topologiju. [ Bojan Basic @ 22.06.2008. 15:52 ] @
Citat: petarm: Ako imam dve baze 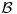 i i 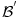 neke topologije neke topologije 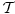 da li vise informacija imam ako radim sa manjom ili vecom bazom? da li vise informacija imam ako radim sa manjom ili vecom bazom?Imaš potpuno iste informacije, jer baza jednoznačno određuje topologiju, a samim tim i sve ostalo što te zanima. [ Vincenity @ 22.06.2008. 16:01 ] @
Nije bas svejedno, treba raditi sa topologijom najmanje kardinalnosti... Informacije su navodno iste, ali na primer kada trazis univerzalni prostor za neku klasu topoloskih prostora nije svejedno koju bazu gledas... Najbolje je najmanje kardinalnosti.
[ Bojan Basic @ 22.06.2008. 16:39 ] @
Pitanje je bilo koliko se razlikuju informacije koje ima, a informacije se ne razlikuju nimalo (što sam obrazložio u prošloj poruci). Ti objašnjavaš šta je praktičnije, a to je sasvim drugo pitanje.
[ h4su @ 22.06.2008. 23:01 ] @
Eh,ko da to nisam nikad ni ucio.Blage veze nemam jel se to vi podsjecate malo ili je do mene :D. [ Vincenity @ 22.06.2008. 23:22 ] @
Pa kako se ne razlikuju informacije. Ako zna da ima jednu bazu odredjene kardinalnosti, moze nesto da uradi, ako ne zna da ima tu bazu te kardinalnosti, ne moze to nesto da uradi...
[ Vincenity @ 22.06.2008. 23:29 ] @
Evo primer :))
Zna se da je kantorova kocka univerzalan prostor za sve nula-dimenzionalne prostore tezine m vece od alef_0. I ako ti imas neki svoj prostor, dok ne nadjes bazu kardinalnosti m ne mozes da znas da li je u kantorovoj kocki ili nije... [ Bojan Basic @ 23.06.2008. 01:36 ] @
Citat: Vincenity: I ako ti imas neki svoj prostor, dok ne nadjes bazu kardinalnosti m ne mozes da znas da li je u kantorovoj kocki ili nije... Svaka baza jednoznačno određuje topološki prostor (to sam već rekao). Dakle, preko koje god baze da mi je prostor dat, mogu dalje da ga ispitujem i, uz manje ili više truda, nađem bazu željene kardinalnosti (ako takva postoji). [ Vincenity @ 23.06.2008. 09:03 ] @
Eto, konacno smo se slozili :))
Naravno da je svejedno koju bazu imas, jer svaka generise istu topologiju, ali da bi dobio neke informacije o prostoru, moras pomocu te koju imas naci neku drugu, najmanje karidnalnosti... Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|