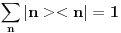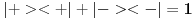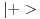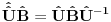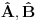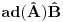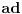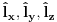[ petarm @ 28.03.2008. 15:57 ] @
|
[ petarm @ 29.03.2008. 16:05 ] @
[ tomkeus @ 08.04.2008. 14:57 ] @
Citat: To je operator koji deluje na operatore. Npr. operatori koji deluju na vektorskom prostoru  i sami čine vektorski prostor i sami čine vektorski prostor 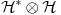 . Superoperatori su operatori koji deluju na ovom vektorskom prostoru. . Superoperatori su operatori koji deluju na ovom vektorskom prostoru.Npr. kada u nekom vektorskom prostoru deluje neki operator 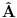 tada je pri preslikavanju bazisa ovim operatorom indukovana transformacija operatora reprezentovana superoperatorom tada je pri preslikavanju bazisa ovim operatorom indukovana transformacija operatora reprezentovana superoperatorom 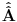 čije dejstvo na neki operator čije dejstvo na neki operator 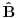 je definisano sa je definisano sa 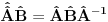 . .Citat: To je pridružena reprezentacija Lijeve algebre. Recimo ako imaš algebru L, tada je pridružena reprezentacija nekog 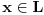 zadata sa zadata sa 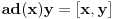 za svako za svako 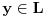 pri čemu je [,] Lijevo množenje u algebri. pri čemu je [,] Lijevo množenje u algebri.Citat: Kako očekuješ bilo kakav odgovor na ovo pitanje? Šta je 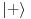 ? ?Citat: petarm: Sta je tacno Kazimirov operator? Nasao sam da je 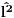 Kazimirov operator. Jel to svaki operator na neki stepen? Kazimirov operator. Jel to svaki operator na neki stepen?Ne. Kazimirov operator neke Lijeve algebre nije element date algebre ali uvek komutira sa svim elementima algebre tako da se obično koristi za klasifikaciju ireducibilnih reprezentacija algebre. Mrzi me da pišem matematičke detalje zato što ih ima dosta, a ako te zanima pogledaj http://bmw.ff.bg.ac.yu/Katedre/QMF/pdf/y2k.pdf i poglavlje o Lijevim algebrama. Citat: petarm: Boze operator 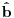 mi smanjuje broj fonona. Za svaki sistem postoji neko osnovno stanje. Kada na njega oddelujem boze operator anihilacije dobicu mi smanjuje broj fonona. Za svaki sistem postoji neko osnovno stanje. Kada na njega oddelujem boze operator anihilacije dobicu  . Kako da znam kada cu dobiti . Kako da znam kada cu dobiti  ako mi osnovno stanje nije eksplicitno zadato? ako mi osnovno stanje nije eksplicitno zadato?Osnovno stanje u reprezentaciji druge kvantizacije ti je uvek 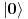 jer je to uvek stanje najniže energije. jer je to uvek stanje najniže energije.[ petarm @ 08.04.2008. 16:40 ] @
[ tomkeus @ 08.04.2008. 16:51 ] @
Citat: petarm: Projektori deluju na 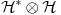 i cine Vajlov bazis. Je li projektor superoperator? Ipak izgleda da nije! i cine Vajlov bazis. Je li projektor superoperator? Ipak izgleda da nije!Jok. Projektori deluju u  i indukuju projektore u i indukuju projektore u 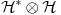 preko preko 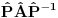 . .[ petarm @ 08.04.2008. 16:57 ] @
[ petarm @ 03.08.2008. 02:09 ] @
ZAD 4.24. y2k
Pokazati da zbog komutacionih relacija operatora koordinate i impulsa dimenzija prostora stanja u kvantnoj mehanici mora biti beskonacna. RES 4.24 Hajzenbergova algebra je razresiva. Voleo bih objasnjenje ovoga ako je moguce. Inace ja sam naisao na sledece 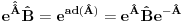 Odakle bi se moglo zakljuciti sledece 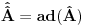 Buni me malo ovo! Jer ja ako imam Lijevu algebru  ima smisla da pricam o ima smisla da pricam o 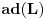 , a operatori se indukuju mnozenjem , a operatori se indukuju mnozenjem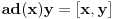 . Ali ja ovde imam . Ali ja ovde imam 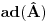 gde je gde je 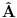 operator? operator?[ petarm @ 08.09.2008. 17:24 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|