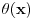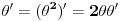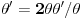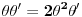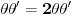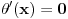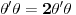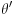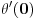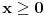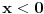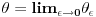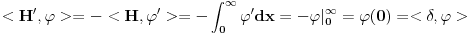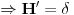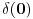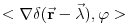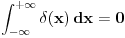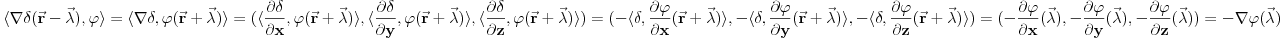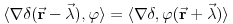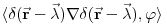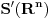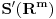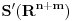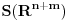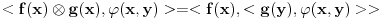[ petarm @ 03.04.2008. 15:36 ] @
|
[ Fitopatolog @ 03.04.2008. 19:39 ] @
U pristupu.
h(x) = h(x)*h(x) samo za x<=0 i x>e, e teži 0+ ( h(x) - Hevisajdova f-ja ) [Ovu poruku je menjao Fitopatolog dana 04.04.2008. u 21:28 GMT+1] [ Fitopatolog @ 03.04.2008. 19:56 ] @
[ Nedeljko @ 04.04.2008. 09:50 ] @
[ petarm @ 04.04.2008. 19:20 ] @
[ Nedeljko @ 05.04.2008. 14:42 ] @
Ja ne znam šta je to distribusioni izvod u tački. Moraš se opredeliti za kontekst onog svog računa. Ja sam ti izveo obrazloženje u klasičnoj analizi. Ako radimo u prostoru distribucija, onda gubi smisao pojam vrednosti u tački. Seti se pojma distribucije. Da, može se ponekad govoriti o vrednosti distribucije u tački, ali ne u opštem slučaju (recimo, može se govoriti o vrednosti Dirakove distribucije u tačkama van nule, ali ne i u nuli). Takođe, distribuciju u opštem slučaju možeš množiti beskonačno diferencijabilnom, a ne bilo kakvom lokalno integrabilnom funkcijom (kao Hevisajdovom funkcijom u tvom slučaju).
Napiši tačan kontekst računa, pa onda da vidimo. [ petarm @ 05.04.2008. 15:16 ] @
Jedna od definicija delta funkcije koja jako dobro radi u praksi je:
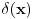 je je  za za 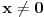 i i  za za  . .Sto bi znacilo 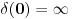 . A pokazao sam da je . A pokazao sam da je 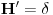 . Pa prema tome zasto ne mogu reci . Pa prema tome zasto ne mogu reci 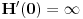 ? ?(Ovaj racun sto sam poslao nije tacan naravno. Nemoj da mislis da ja tvrdim da je  .) .)Postavlja se pitanje sta ce nam distribucije ako se sve stvari mogu dobiti klasicnom analizom. Pa ocigledno nam onda ne bi trebale. Moje pitanje je da li ti smatras da je dovde sve OK? 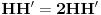 [ Nedeljko @ 05.04.2008. 16:05 ] @
Citat: petarm: Jedna od definicija delta funkcije koja jako dobro radi u praksi je Šta to znači "dobro radi u praksi"? Jeli matematički korektna ili nije? Originalno je Dirakova funkcija bila definisana kao funkcija koja je u svim tačkama van nule jednaka nuli, a integral joj je jednak jedinici. Takva funkcija ne postoji u Lebegovom zasnivanju pojma integrala (što se vrlo lako dokazuje). Kasnije je pronađen formalizam u koji će se uklopiti primene Dirakove funkcije. Međutim, tu se više ne govori o Dirakovoj funkciji, već distribuciji definisanoj sa 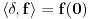 za svaku osnovnu funkciju  . To je jedina korektna definicija koju ja znam. Da, postoji pojam vrednosti distribucije u tački, ali koji neće biti definisan za svaku distribuciju u svakoj tački. Dobro, jeste . To je jedina korektna definicija koju ja znam. Da, postoji pojam vrednosti distribucije u tački, ali koji neće biti definisan za svaku distribuciju u svakoj tački. Dobro, jeste 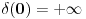 i i 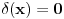 za za 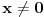 . .Odgovor na tvoje pitanje je: 1. Jednakost 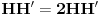 jeste tačna u kontekstu klasične analize, s tim što u tački jeste tačna u kontekstu klasične analize, s tim što u tački  nijedna od strana nije definisana. nijedna od strana nije definisana.2. Jednakost 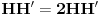 nema smisla u kontekstu teorije distribucija, jer se vrši množenje prave distribucije nema smisla u kontekstu teorije distribucija, jer se vrši množenje prave distribucije 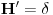 (koja se ne svodi na običnu funkciju) nečim što nije beskonačno diferencijabilna funkcija, što u teoriji distribucija nije definisano. (koja se ne svodi na običnu funkciju) nečim što nije beskonačno diferencijabilna funkcija, što u teoriji distribucija nije definisano.[ petarm @ 05.04.2008. 17:17 ] @
Citat: Nedeljko: Šta to znači "dobro radi u praksi"? Vidis matematika sama za sebe bas i nema smisla. Da nigde nije nasla primenu ne bi ni postojala. Ti recimo u kvantnoj fizici mozes da definises potencijal kao 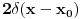 ... Itd. Za ovakve probleme iz prakse ova definicija radi. ... Itd. Za ovakve probleme iz prakse ova definicija radi. Citat: Nedeljko: Originalno je Dirakova funkcija bila definisana kao funkcija koja je u svim tačkama van nule jednaka nuli, a integral joj je jednak jedinici. Da i zaboravio si da joj je u originalnoj definiciji u  data vrednost data vrednost  . . Citat: Nedeljko: Jeli matematički korektna ili nije? Ja ne brinem bas toliko da li je nesto formalno dobro definisano ako mi to ne pravi nekih vecih problema. Ne trazim bas dlake u svakom problemu...U nekima da. Citat: Nedeljko: Međutim, tu se više ne govori o Dirakovoj funkciji, već distribuciji definisanoj sa 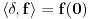 za svaku osnovnu funkciju  . . 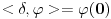 Mozes to i ovako zapisati 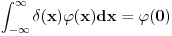 i onda kazes Dirakova  funkcija ukida integral. funkcija ukida integral. Sta mislis o ovom definiciji  funkcije? funkcije?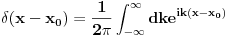 [ Nedeljko @ 05.04.2008. 18:08 ] @
Citat: petarm: Vidis matematika sama za sebe bas i nema smisla. Da nigde nije nasla primenu ne bi ni postojala. Ti recimo u kvantnoj fizici mozes da definises potencijal kao 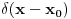 ... Itd. Za ovakve probleme iz prakse ova definicija radi. ... Itd. Za ovakve probleme iz prakse ova definicija radi.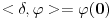 Sa ovim stavom se ne bih složio, ali nema potrebe da o tome ovde polemišemo jer to zalazi u filozofiju i nema veze sa ovom temom. Citat: petarm: Za ovakve probleme iz prakse ova definicija radi. E, pa vidiš, za probleme kao što je ovaj o kome se diskutuje na ovoj temi ne radi. Matematika ti daje aparat u koji ćeš moći da se pouzdaš u svim njegovim interpretacijama, uz jedini uslov da se strogo pridržavaš pravila. Pa, pridržavaj ih se ili nemoj postavljati pitanja kao što je ono iz prve poruke na ovoj temi, jer ti matematika onda ništa i ne garantuje. Citat: petarm: Da i zaboravio si da joj je u originalnoj definiciji u data vrednost  . .Nisam ništa zaboravio, niti znam da li je taj uslov uključen u originalnu Dirakovu definiciju. Uslov koji "Dirakovoj funkciji" daje beskonačnost u nuli glasi 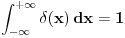 , obzirom da je , obzirom da je 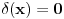 za za 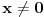 . No, to je sve besmisleno u Lebegovom zasnivanju integralnog računa. . No, to je sve besmisleno u Lebegovom zasnivanju integralnog računa.Drugim rečima, taj uslov ne menja ništa. Neka je 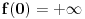 i i 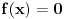 za za 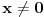 . Ako sa . Ako sa 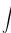 označimo Lebegov integral, biće označimo Lebegov integral, biće 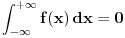 . Obnovi Lebegov integral. Njegova vrednost se ne menja promenom vrednosti podintegralne funkcije u jednoj tački, makar ta vrednost bila i . Obnovi Lebegov integral. Njegova vrednost se ne menja promenom vrednosti podintegralne funkcije u jednoj tački, makar ta vrednost bila i 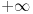 . Ako je . Ako je 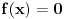 svuda osim eventualno u jednoj tački, onda je svakako svuda osim eventualno u jednoj tački, onda je svakako 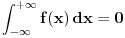 bez obzira na vrednost bez obzira na vrednost  u toj jednoj tački, bila ona konačna ili beskonačna. u toj jednoj tački, bila ona konačna ili beskonačna.Citat: petarm: Ja ne brinem bas toliko da li je nesto formalno dobro definisano ako mi to ne pravi nekih vecih problema. Ne trazim bas dlake u svakom problemu...U nekima da. Zato i imaš problema kao što je onaj sa početka teme. Citat: Samo ako uvedeš novu teoriju integracije u kojoj to može da prođe. U Lebegovoj jok. Ne može se u matematici samo mućkati izrazima bez vođenja računa o njihovom značenju. Ja simbol  interpretiram kao Lebegov integral i tu ovo što si napisao ne prolazi. Ako imaš neku drugu definiciju integrala, navedi je, pa da vidimo. interpretiram kao Lebegov integral i tu ovo što si napisao ne prolazi. Ako imaš neku drugu definiciju integrala, navedi je, pa da vidimo.Citat: Ako se misli na Lebegov integral, besmislena je. Ako ne, onda je nepotpuna, jer joj fali značenje simbola  . .[ Nedeljko @ 05.04.2008. 18:15 ] @
[ petarm @ 05.04.2008. 19:00 ] @
[ Nedeljko @ 05.04.2008. 20:12 ] @
[ petarm @ 05.04.2008. 21:20 ] @
[ Nedeljko @ 06.04.2008. 10:10 ] @
Citat: Neka je 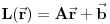 , gde je , gde je  konstantna inverzibilna matrica, a konstantna inverzibilna matrica, a 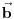 konstantan vektor. Tada se kompozicija konstantan vektor. Tada se kompozicija 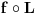 , gde je , gde je  proizvoljna distribucija, definiše kao distribucija za koju je proizvoljna distribucija, definiše kao distribucija za koju je 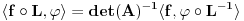 za svaku test funkciju za svaku test funkciju  . .Citat: U klasičnoj analizi Furijeova transformacija od  nije definisana. nije definisana.Citat: Da. Proizvod  nije definisan. nije definisan.[Ovu poruku je menjao Nedeljko dana 06.04.2008. u 12:44 GMT+1] [ toplim @ 06.04.2008. 10:31 ] @
Ili jos prostije:
0*X=2 X=2/0 A to nema smisla. Mislim stvarno nema smisla. A to da nema smisla ne odgovara bas matematici kao nauci, tako da predlazem matematicarima da izmisle neki novi broj. Recimo beskonacno na faktorijel beskonacno :) a jos mi nesto pade na pamet: 1*1=1 2*2=4 3*3=9 4*4=16 5*5=25 ... Za koliko se razlikuju proizvodi: 4-1=3 9-4=5 16-9=7 25-16=9 ... znaci niz nepanih brojeva...pa ako matematicki nastavimo niz dobijemo da je 0*0= 0, hm sto i jeste tacno:) [ Nedeljko @ 06.04.2008. 11:48 ] @
Citat: toplim: Ili jos prostije: 0*X=2 X=2/0 A to nema smisla. Mislim stvarno nema smisla. A to da nema smisla ne odgovara bas matematici kao nauci, Zašto "ne odgovara"? [ toplim @ 06.04.2008. 13:25 ] @
Zato sto je matematika najstarija nauka, valjda. I ako u matematici postoje nemoguce stvari, kako onda uopste doci do nekog prakticnog otkrica baziranog na matematici, kad nam samo sredstvo (matematika) postavlja granice?
Mislim, vidim da je moguce, ali kazem ne bi trebalo da postoje te granice. Da nisu izmisljeni kompleksni brojevi nikom ne bi palo na pamet da mozda postoje paralelni svetovi, pa se danas vrse neka naucno filozofska istrazivanja na tom polju :) [ petarm @ 06.04.2008. 13:38 ] @
Citat: toplim: Da nisu izmisljeni kompleksni brojevi nikom ne bi palo na pamet da mozda postoje paralelni svetovi, pa se danas vrse neka naucno filozofska istrazivanja na tom polju :) Ideja paralelnih svetova nema veze sa kompleksnim brojevima! [ petarm @ 06.04.2008. 13:43 ] @
Citat: Nedeljko: Da. Proizvod  nije definisan. nije definisan.[Ovu poruku je menjao Nedeljko dana 06.04.2008. u 12:44 GMT+1] Vidis mislim da to nije tacno. Ti mozes da mnozis  nizove i pustiti limes. A siguran sam da se u teoriji distribucija definise i proizvod distribucija. nizove i pustiti limes. A siguran sam da se u teoriji distribucija definise i proizvod distribucija. [ petarm @ 06.04.2008. 13:48 ] @
Citat: toplim: Zato sto je matematika najstarija nauka, valjda. I ako u matematici postoje nemoguce stvari, kako onda uopste doci do nekog prakticnog otkrica baziranog na matematici, kad nam samo sredstvo (matematika) postavlja granice? David Hilbert je u prvoj polovini proslog veka otvarao neku veliku inzenjersku konferenciju u Getingemu. I zavrsio je govor time sto je rekao da matematika i tehnika ne mogu biti u sukobu jer tehnika nema veze sa matematikom. [ toplim @ 06.04.2008. 13:49 ] @
Citat: petarm: Ideja paralelnih svetova nema veze sa kompleksnim brojevima! Ih, pa kako nema. U pocetku nije bilo, ali ako iskopas dalje ima veze i te kako. Realna ravan predstavlja materiju a imaginarna antimateriju. Pa vremenska osa po kojoj se krece trodimenzionalni svet. Sve je to brate povezano, a koliko je tacno to ne znam, vreme ce pokazati. Mada, to nije tema, izvinjavam se. [ petarm @ 06.04.2008. 13:52 ] @
Citat: toplim: Ili jos prostije: 0*X=2 X=2/0 A to nema smisla. Mislim stvarno nema smisla. A to da nema smisla ne odgovara bas matematici kao nauci, tako da predlazem matematicarima da izmisle neki novi broj. Recimo beskonacno na faktorijel beskonacno :)  nije broj. nije broj. [ toplim @ 06.04.2008. 15:29 ] @
Pa ni imaginarni broj (i) nije broj, pa ga zovu broj.
A ja u prvoj polovini ovog veka kazem da matematika ima veze sa tehnikom, ali samo u analitickom smislu. [ petarm @ 06.04.2008. 17:07 ] @
[ petarm @ 06.04.2008. 17:09 ] @
Citat: petarm: Vidis mislim da to nije tacno. Ti mozes da mnozis  nizove i pustiti limes. A siguran sam da se u teoriji distribucija definise i proizvod distribucija. nizove i pustiti limes. A siguran sam da se u teoriji distribucija definise i proizvod distribucija.Pogledacu ovo kad stignem! Mozda i danas. [ Nedeljko @ 06.04.2008. 19:27 ] @
@toplim
Kada neki aparat ne bi imao nikakva ograničenja, ne bi bilo ni ograničenja u proizvodnji gluposti koje taj aparat može da izbaci. Poenta je u tome da dobijaš samo tačne iskaze, što je ograničenje (željeno) samo po sebi, a da bi imao to ograničenje, svakako da moraš imati nekakva ograničenja u osnovama tog aparata koja rezultuju željenim ograničenjem. No, manimo se filozofije. Ako ti baš smeta što u matematici ponešto nedefinisano, i tome ima leka. Može se uvesti posebna konstanta, koja znači "nedefinisano". Obično se obeležava sa 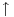 . Znači, . Znači, 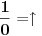 . Međutim, onda celu matematiku moraš da izlažeš na taj način. Onda ni jednakost neće više biti ono što je nekad bila, jer ako sa . Međutim, onda celu matematiku moraš da izlažeš na taj način. Onda ni jednakost neće više biti ono što je nekad bila, jer ako sa 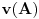 označimo istinitosnu vrednost iskaza označimo istinitosnu vrednost iskaza  , onda će biti , onda će biti 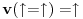 , a ne , a ne 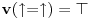 , gde je , gde je 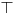 oznaka za "tačno". No, na taj način možeš izložiti celu matematiku, ali time ništa ne dobijaš i ništa ne gubiš. Dobija se potpuno ista matematika, samo malo drugačije zapisana. oznaka za "tačno". No, na taj način možeš izložiti celu matematiku, ali time ništa ne dobijaš i ništa ne gubiš. Dobija se potpuno ista matematika, samo malo drugačije zapisana.[ toplim @ 06.04.2008. 19:46 ] @
Slazem se sa tobom Nedeljko.Nisam ja ko neki sto zabede pa nikako da stanu dok ne isteraju svoje.
Ali ako znamo, kolika je prosecna velicina univerzuma i brzinu svetlosti mozemo beskonacno da predstavimo vremenom koje je potrebno da svetlost predje sa jednog kraja na drugi kraj. Mada to nema veze s matematikom. I da, beskonacno jeste uvek beskonacno ma kako da ga pisali. Ali govorim o nedefinisanom! I ono sto je 1 realnom prostoru, to je (i) u imaginarnom, zar postoje samo dva prostora? Moze se na isti nacin predstaviti i invremenski (inverzno vremenski) prostor i vremenski. A to su ukupno 4 prostora i to samo ako za osnovu uzmemo hipotezu da se nulta vremenska tacka nalazi u nuli i da je ravna crnoj rupi. Odgovara krstu sa 4 odvojena prostora koji je najduze opstao. U takvom animiranom prostoru je vrlo lako predstaviti svaku prirodnu pojavu ili proces, pa sam mislio eto korisnosti uvodjenja jos nekih nedefinisanih pojmova u matematici. Po toj analogiji 1/0 vise nije nedefinisano vec odgovara dijagonali koju provucemo od 1 ka inverzno vremenskom prostoru.Odnosno od tacke 1 do tacke (iv) i onda tacka iv predstavlja preslikanu tacku 1 u inverzno vremenskom prostoru. Malo filozofi malo naucnici...sta ja znam tako nesto... [ Nedeljko @ 06.04.2008. 19:55 ] @
Ti mora da si se naslušao gluposti onog Đure Koruge ili nekog njemu sličnog. Sve ovo što pišeš nema nikakve veze ni sa matematikom ni sa fizikom. Bez uvrede, ali o čemu ti uopšte pričaš? Znaš li uopšte kontekst tih stavova, ako kontekst uopšte postoji?
[ toplim @ 06.04.2008. 20:10 ] @
Ne znam za tog Djuru, ja sam automehanicar.
Ali i Tito je bio automehanicar :) Pokusaj da shvatis. U trodimenzionalnom prostoru ne postoji koordinata koja bi pokazivala vreme, a da pri tome ne dodje do poklapanja. Ako se prihvati hipoteza krsta, dolazimo i do kordinata za vreme i inverznovreme (ne negativno vreme vec inverzno)koje uprosceno predstavlja vreme koje jos nije doslo racunajuci od beskonacnosti pa do nulte tacke. Odnosno nulta tacka vremena je isto sto i beskonacnost inverznog vremena, i obratno. A onda sva 4, 3d prostora animirano predstaviti i dolazimo do vrlo interesantnih otkrica, odnosno do potvrde mnogih vec dokazanih zakona. I ponavljam, u takvom prostoru je moguce predstaviti svaku pojavu ili proces. Znam sta pricam, ali ne mogu sada na kompu da nadjem tu animaciju 12d prostora, onda bih se setio jos necega a tesko je sve zamisliti. I da dodam, dolazimo do otkrica recimo, da je + i - beskonacno jedna ista stvar, da svi procesi teze da zatvore pravilan krug u takvom prostoru. I do saznanja da je sve povezano i da tece po zakonu linearnosti. Hm, sad vidim Djuro je neki doktor. Ne znam sad, sta mu znaci g, valjda gravitaciona sila, previse je uprostio. Ovakav prostor predstavlja samo potvrdu prirodnih proces, e sad ne znam kako je definisao ljudsku dusu, kakav je to proces, mozda inverzno vremenski, pa se onda mozda moze doci do toga da je dusa=4g Procitacu! [ Fitopatolog @ 06.04.2008. 20:48 ] @
TopliM, napravimo sledeći misaoni eksperiment razmatrajući rad jednog cilindra sa klipom u
a) dvodimenzionalnom b) trodimenzionalnom i c) četvorodimenzionalnom prostoru. Tačka b) - trodimenzionalni slučaj - je sasvim jasan i ne moramo ga detaljnije elaborirati. Tačka a) - Kod dvodimenzionalnog prostora imamo samo širinu i dužinu, bez visine. Dakle - motor, cilindar i klip, automehaničar, garaža, itd. - svi su u ravni i imaju samo dve dimenzije. Naravno, oni to ne znaju, misle da je njihov svet savršen i ne primećuju da im nedostaje treća dimenzija, baš kao što i nama ne nedostaje četvrta dimenzija. Nije teško zamisliti kako izgleda cilindar sa klipom u dvodimenzionom sistemu - manji pravougaonik kliže unutar većeg pravougaonika. Međutim, dvodimenzionalni automehaničar ne može da vidi ono što vidi trodimenzionalni - a to je kako smesa u cilindru sagoreva (i to bez rastavljanja motora!). Tačka c) - Analogno prethodnoj tački, četvorodimenzionalni automehaničar vrlo lako može da vidi kako se vrši sagorevanje u trodimenzionalnom cilindru, bez rasklapanja motora. Malo je čudno za nas kako kroz tu rupu motor ne gubi kompresiju, ali ne zaboravite da se radi o četvrtoj dimenziji. Naravno, diskusija se može nastaviti i dalje, dodajući petu, šestu, itd. dimenziju. [ Nedeljko @ 06.04.2008. 20:54 ] @
Citat: toplim: Ali i Tito je bio automehanicar :) Mašinbravar, ali nije bitno. Citat: toplim: Ako se prihvati hipoteza krsta, Koja hipoteza? Nikad čuo. Citat: toplim: Odnosno nulta tacka vremena je isto sto i beskonacnost inverznog vremena, i obratno. Ovo mogu da shvatim samo kao obrtanje smera proticanja vremena. Citat: toplim: A onda sva 4, 3d prostora Da si učio vektorske prostore, znao bi da u 4D prostoru možeš naći beskonačno mnogo 3D potprostora. Citat: toplim: I do saznanja da je sve povezano i da tece po zakonu linearnosti. Jeli je i slobodan pad tela u Zemljinom gravitacionom polju linearan. A kosi hitac? [ petarm @ 06.04.2008. 21:15 ] @
[ toplim @ 06.04.2008. 21:44 ] @
Fitopatolog...nemam sta da dodam.
Ok za Tita :) Hipoteza krsta je moja hipoteza, imam prava na to. toplim: Odnosno nulta tacka vremena je isto sto i beskonacnost inverznog vremena, i obratno. Ovo mogu da shvatim samo kao obrtanje smera proticanja vremena. Pa u principu da, ali ne od danasnjeg dana (0) pa do postanka, vec od beskonacnosti ka danasnjem danu. Vektorske prostore ucio jesam, kao sto u dvodimenzionalnom prostoru postoji beskonacno tacaka, ako uzmemo da tacka predstavlja jednodimenzioni prostor odnosno skalar. A zasto da koristimo sve te prostore? Ja predlazem 4 3d prostora iz prakticnih razloga, jer je danas to lako animirati, a nekad kad budu hologrami realna i siroko primenjliva naprava, mozemo govoriti i o drugim prostorima koji nam za sada ne trebaju. Slobodan pad tela nije linearan proces u 3d prostoru. Zasto? Zato sto nam sat otkucava jednakom brzinom, a isti se nalazi u nasem 3d prostoru, tako da nije realna referentna tacka. Ali ako ukljucimo i vreme i "hipotezu-teoremu" da vreme tece nelinearno, onda slobodan pad jeste linearan proces. Kosi hitac zahteva jos jedan prostor, tj + inverznovremenski prostor i u tom sistemu i kosi hitac je linearan. A u 4d prostoru kosi hitac je parabola ili hiperbola, nisam siguran, uglavnom je to kriva viseg reda od krive u 3d prostoru. Ili, kao sto znamo da se svetlost ne krece pravolinijski vec zakrivljuje.To je zato sto imamo uticaj 4 dimenzije vremena, koju pokusavamo da uzimamo kao referntnu tacku. A opet ako tu dodamo iv prostor, dolazimo da se svetlost prostire linijom kruznice. Odnosno na osnovu zakrivljenosti svetlosnog zraka mozemo izracunati velicinu univerzuma. Ipak, da se vratim na temu 1=1 [Ovu poruku je menjao toplim dana 06.04.2008. u 23:25 GMT+1] [ petarm @ 07.04.2008. 08:07 ] @
Ajde molim te otvori posebno neku temu pa pisi o svojim hipotezama...
[ Nedeljko @ 07.04.2008. 11:12 ] @
Citat: Tako je. Ali to nema veze sa mnozenjem tipa f(x)g(x), nego sa proizvodom tipa f(x)g(y). To je druga stvar. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|