[ milosmcse @ 07.04.2008. 22:32 ] @
| Potrebno je dokazati tj da vazi ili ne vazi sledeca relacija (prakticno gledano ona je tacna) ali kako da to formalno dokazem ;) evo relacije  [Ovu poruku je menjao milosmcse dana 08.04.2008. u 11:18 GMT+1] |
|
[ milosmcse @ 07.04.2008. 22:32 ] @
[ nikmil @ 08.04.2008. 15:55 ] @
Kad smo vec kod skupova i kardinalnosti, i meni treba pomoc :)
Ako je dat otvoren interval (0,1) i skup tacaka S={(x,y) takvo da je 0<x,y<1}, naci: a) 1-1 funkciju f: (0,1) -> S. b) 1-1 funkciju S -> (0,1) Pod a) sam rijesio, npr. f(a) = (a, 0.5), a € (0,1). Pod b)... ne znam. Jel moze neki hint. PS. Izvinjavam se na improvizovanoj notaciji, nisam jos naucio LATEX. [ Nedeljko @ 09.04.2008. 13:14 ] @
[ nikmil @ 09.04.2008. 17:04 ] @
Super! I u knjizi u kojoj sam vidio ovaj zadatak bio je hint da treba primjeniti decimalnu (ili binarnu, nije bitno) ekspanziju. Ja sam nasao neko "geometrijsko" resenje.
Neka je f: S -> (1,+beskonacno) kao na slici. Tad je f((x,y)) = a € R. Neka je g(a) = 1/a. Posto je a>1, onda 0<g(a)<1. Pa je g(a)=g(f((x,y))), odnosno g o f: S -> (0,1). Funkcija je 1-1, posto 1/(a_1) = 1/(a_2) => a_1 = a_2 => (x_1,y_1) = (x_2),(y_2). Funkcija nije "NA" jer, A' nije elemenat f(S), pa prema tome 1/A' nije elemenat g o f(S). [ nikmil @ 09.04.2008. 17:20 ] @
Ali sad imam novi problem :(
Neka je S skup svih n-torki od nula i jedinica, tj. S = { (a_1, a_2, a_3,...) | a_n = 0 ili 1}. Npr (1,1,0,1,0,0...) i (1,1,1,1,0...) su elementi S. Dokazati da je S neprebrojiv. Ja sam ovako radio: neka je A = (a_1, a_2, ..., a_n). (Svi elementi skupa S su oblika A). Tada imamo funkciju f: S -> N definisanu na sledeci nacin: f(A) = 5 a_1 a_2 a_3 ... a_n, tj. prva cifra je 5, druga cifra je a_1, itd. Za prvu cifru se moze uzeti bilo koja cifra, ne mora 5, ali se mora uzeti neka da ne bi imali problema ako je a_1 = 0. Ocigledno je da je f(A) elemenat N. Sad imamo: ako je f(A1) = f(A2) <=> 5 a_1 a_2 a_3 ... a_n = 5 b_1 b_2 ... b_m => 1) n=m, jer dva prirodna broja koja nemaju isti broj cifara ocigledno nisu jednaka. 2) => 5 = 5 i a_1=b_1 i ... i a_n = b_m => (a_1, a_2, ..., a_n) = (b_1, b_2, ... b_m) => A1 = A2, tj. f: S-> N je 1-1, pa imamo da je card S =< card N, a posto je N prebrojiv, to S mora biti ili prebrojiv ili konacan. Posto ocigledno nije konacan onda je prebrojiv. Evo i postavke zadatka na engleskom, posto postoji mogucnost da sam ga lose preveo. Exercise 1.5.4. Let S be the set consisting of all sequences of 0’s and 1’s. Observe that S is not a particular sequence, but rather a large set whose elements are sequences; namely, S = {(a1, a2, a3, . . . ) : an = 0 or 1}. As an example, the sequence (1, 0, 1, 0, 1, 0, 1, 0, . . . ) is an element of S, as is the sequence (1, 1, 1, 1, 1, 1, . . . ). Give a rigorous argument showing that S is uncountable. Gdje pravim gresku? [ Bojan Basic @ 09.04.2008. 17:43 ] @
Citat: nikmil: Pod a) sam rijesio, npr. f(a) = (a, 0.5), a € (0,1). Ovo nije dobro rešenje, jer funkcija nije bijekcija (npr. element 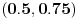 nema svoj original). nema svoj original).Citat: I ovo je pogrešno: element 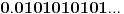 nema svoj original. Slična ideja može da prođe, ali je treba malo doraditi. nema svoj original. Slična ideja može da prođe, ali je treba malo doraditi.Citat: Nisi objasnio kako si definisao funkciju (tj. šta su ove krive linije na slici). Citat: nikmil: Gdje pravim gresku? Greška je u tome što je  skup beskonačnih nizova (u tom slučaju ova tvoja funkcija očigledno ne pomaže). skup beskonačnih nizova (u tom slučaju ova tvoja funkcija očigledno ne pomaže).[ Nedeljko @ 10.04.2008. 08:14 ] @
Bojane, nisu se ni trazile bijekcije, vec 1-1 preslikavanja.
[ nikmil @ 10.04.2008. 09:41 ] @
Da, trebala su mi 1-1 preslikavanja. Ako imamo 1-1 preslikavanje S->(0,1) i drugo (0,1)->S, onda postoji i bijekcija S<->(0,1) (Šreder-Bernštajnova teorema). Znači da je card S = card (0,1). To mi je trebalo da dokažem.
Što se tiče ovog "geometrijskog" rešenja, ideja mi je bila da svaku tačku (x,y) gdje je x+y=n, 0<n<2, preslikam u neki interval (a, a + n*sqrt(2)), gdje je a>1. Pošto x+y=n, s datim ograničenjima 0<x,y<1, opisuje duž dužine n*sqrt(2) bez krajnjih tačaka (n,0) i (0,n) (ili duž dužine (2-n)*sqrt(2), u slučaju da je n>1), onda se može naći bijekcija koja preslikava tu duž u duž jednake dužine na osi x. Tako za neko n1 tačke (x,y) gdje je x+y=n1 preslikamo u neki interval jednake dužine na osi x, tj. u (a, a+n1*sqrt(2)), pa za sledeće n2 tačke (x,y), x+y=n2 preslikamo u novi interval na osi x, ali ga malo "odmaknemo" od prethodnog intervala tako da nemaju presjek. Takva funkcija je 1-1 preslikavanje (x,y) u neko m>1. Sad napravimo novu funkciju koja preslikava m u 1/m. Kompozicija ove dvije funkcije je 1-1 funkcija S->(0,1). Znam da ovo nije baš rigorozno, ali uz malu doradu moglo bi biti. Tako da ove krive na slici ne prestavljaju nikakvu funkciju, nego samo pokazuju da se tačka A preslikava u A'. Zaboravio sam da im dodam strelicu na kraju :) Izvinjavam se. Što se tiče ovog drugog zadatka, tek sam kasnije provalio da "sequence" znači niz :) Ja sam prvo kontao da su u pitanju n-torke, i da n u tom slučaju mora biti konačan broj. Evo rešenja: Pretpostavimo da je S prebrojiv. Onda postoji bijekcija f: N->S. N S 1 -> f(1) = (a11, a12, a13, a14, ...) 2 -> f(2) = (a21, a22, a23, a24, ...) 3 -> f(3) = (a31, a32, a33, a34, ...) ... Sad definišimo b = (b1, b2, b3 ...) gdje je b_i = 0, ako je aii=1 ili b_i=1, ako je aii = 0. Tada b nije jednako a_n, za n iz N, jer b = a_n <=> (b1, b2, b3,..., bn,...) = (a_n1, a_n2, ..., a_nn,....) <=> b1=a_n1 i ... i bn = a_nn. Međutim ako je a_nn = 1 onda je bn=0 i obrnuto, pa sledi da bn nije jednako a_nn, tj. b nije jednako a_n, pa b nije elemenat f(N). Očigledno je da je b elemenat S, i kako b nema svoj orginal, funkcija f nije bijekcija. S je neprebrojiv. Hvala svima još jednom. Ovi skupovi znaju da budu baš naporni. [ Bojan Basic @ 10.04.2008. 10:55 ] @
Izvinjavam se za ove bijekcije, loše sam pročitao. Svejedno, sad kad sam već pominjao doradu Nedeljkove ideje, napisaću kako se stvarno može napraviti bijekcija — tako u jednom potezu rešavamo i a) i b), a još se ne moramo pozivati na Kantor—Šreder—Bernštajna.
Naime, ako 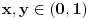 i i 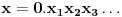 i i 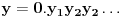 , podelimo ova dva broja na „blokove“ tako što ćemo posle svake nule povući granicu. Recimo, ako je , podelimo ova dva broja na „blokove“ tako što ćemo posle svake nule povući granicu. Recimo, ako je 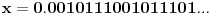 , podelili bismo ga kao , podelili bismo ga kao 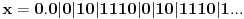 . Sada, ukoliko je . Sada, ukoliko je 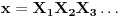 i i 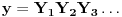 , gde su , gde su 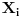 i i 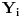 blokovi, definišemo blokovi, definišemo 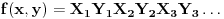 . .Citat: nikmil: Što se tiče ovog "geometrijskog" rešenja, ideja mi je bila da svaku tačku (x,y) gdje je x+y=n, 0<n<2, preslikam u neki interval (a, a + n*sqrt(2)), gdje je a>1. Pošto x+y=n, s datim ograničenjima 0<x,y<1, opisuje duž dužine n*sqrt(2) bez krajnjih tačaka (n,0) i (0,n) (ili duž dužine (2-n)*sqrt(2), u slučaju da je n>1), onda se može naći bijekcija koja preslikava tu duž u duž jednake dužine na osi x. Tako za neko n1 tačke (x,y) gdje je x+y=n1 preslikamo u neki interval jednake dužine na osi x, tj. u (a, a+n1*sqrt(2)), pa za sledeće n2 tačke (x,y), x+y=n2 preslikamo u novi interval na osi x, ali ga malo "odmaknemo" od prethodnog intervala tako da nemaju presjek. Sad je jasnije šta si hteo, ali bojim se da nije dobro. Naime: recimo da duž 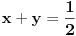 preslikaš u preslikaš u 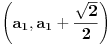 a duž a duž 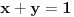 u u 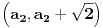 , i neka je , i neka je 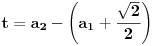 . Sada sve duži . Sada sve duži 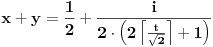 gde je gde je 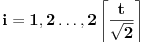 treba da smestiš u interval treba da smestiš u interval 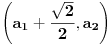 (jer važi (jer važi 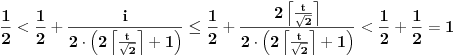 ). Međutim, dužina ovog intervala je ). Međutim, dužina ovog intervala je  , a za ukupnu dužinu svih navedenih duži važi , a za ukupnu dužinu svih navedenih duži važi 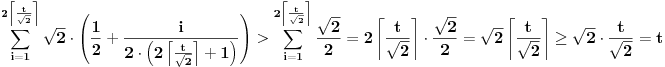 , što je kontradikcija. , što je kontradikcija.Štaviše, ovakva ideja s prebacivanjem duži suštinski je pogrešna iz sledećeg razloga: međusobno disjunktnih intervala na realnoj osi ima najviše prebrojivo mnogo (to je lako videti: svaki od njih može se jedinstveno odrediti nekom racionalnom tačkom koja mu pripada), dok razmatranih duži ima neprebrojivo mnogo. [ nikmil @ 10.04.2008. 12:59 ] @
Jasno mi je. Gledao sam na Wikipediji Peanovu krivu: [img]http://upload.wikimedia.org/wikipedia/commons/6/64/Peanocurve.svg[/img] pa mi je palo na pamet da početak fiksiram za tačku (0,0), a kraj uhvatim pa razvučem po x-osi :) Ali nisam znao kako da tome dam neku matematičku interpretaciju, pa sam probao sa ovim "x+y=n".
[ Nedeljko @ 11.04.2008. 08:46 ] @
Peanove krive nisu 1-1. Ne postoji neprekidna bijekcija segmenta [0,1] u skup [0,1]2 niti neprekidno 1-1 preslikavanje skupa [0,1]2 u segment [0,1].
[ Nedeljko @ 11.04.2008. 11:03 ] @
Neka
 bijektivno neprekidno preslikavanje i neka je bijektivno neprekidno preslikavanje i neka je 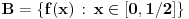 . Skup . Skup  je kompaktan kao neprekidna slika kompaktnog skupa, a posto je u pitanju bijekcija on je takodje i pravi podskup kodomena, pa kao zatvoren pravi podskup kodomena ima neprazan rub. Stavise, zbog beskonacnosti skupa je kompaktan kao neprekidna slika kompaktnog skupa, a posto je u pitanju bijekcija on je takodje i pravi podskup kodomena, pa kao zatvoren pravi podskup kodomena ima neprazan rub. Stavise, zbog beskonacnosti skupa 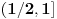 rub skupa rub skupa  ne moze da se svede na samo jednu tacku. Stoga postoji niz ne moze da se svede na samo jednu tacku. Stoga postoji niz 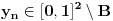 koji konvergira nekoj tacki koji konvergira nekoj tacki 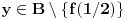 Neka je Neka je 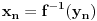 Jasno je da Jasno je da 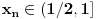 . Zbog kompaktnosti skupa . Zbog kompaktnosti skupa 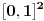 niz niz  ima bar jednu tacku nagomilavanja, na primer ima bar jednu tacku nagomilavanja, na primer  iz iz 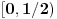 sto je nemoguce. sto je nemoguce.Neka je 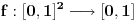 neprekidno 1-1 preslikavanje. Definisimo skupove neprekidno 1-1 preslikavanje. Definisimo skupove 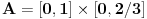 , , 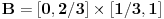 , , 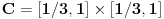 . Slike ovih skupova su, kao neprekidne slike povezanih skupova, povezani skupovi, to jest intervali. Posto je . Slike ovih skupova su, kao neprekidne slike povezanih skupova, povezani skupovi, to jest intervali. Posto je  1-1i preseci ovih skupova su beskonacni, bice beskonacni i preseci njihovih slika. No odatle sledi da slika jednog od skupova 1-1i preseci ovih skupova su beskonacni, bice beskonacni i preseci njihovih slika. No odatle sledi da slika jednog od skupova 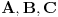 sadrzi presek slika preostala dva, na primer sadrzi presek slika preostala dva, na primer 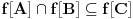 Medjutim, posto je Medjutim, posto je  1-1, odatle sledi da je 1-1, odatle sledi da je 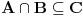 sto ocigledno nije tacno. sto ocigledno nije tacno.Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|