Ajde... pocni :)

Hajde da pocnem :)

2.) Resavamo SJ u datim oblastima. U oblasti . To je naravno za





U oblasti









_{[Ovu poruku je menjao petarm dana 10.04.2008. u 11:37 GMT+1]}

Za oblast je vrednost potencijala .



Kako je iz uslova zadatka imamo da je





Na osnovu Sturm Liuvilove teoreme na granici izmedju oblasti i imamo neprekidnost za talasne funkcije i prve izvode posto je skok potencijala konacan.

Nadam se da negde nisam pogresio!

<sub>[Ovu poruku je menjao petarm dana 10.04.2008. u 16:42 GMT+1]

[Ovu poruku je menjao petarm dana 10.04.2008. u 16:42 GMT+1]

[Ovu poruku je menjao petarm dana 10.04.2008. u 16:43 GMT+1]</sub>

Treci zadatak da probam: Za 2D LHO su sopstvene vrednosti energije : E je konstanta*(1+nx+ny) tj. zbir energija 1D LHO (x)+ 1D LHO(y).
Osnovno stanje je nx=0 , ny=0
I pobudjeno stanje je dvostruko degenerisano : nx=1 , ny=0 ; nx=0 , ny=1
II pobudjeno stanje je trostruko degenerisano : nx=0, ny=2 ; nx=1. ny=1 ; nx=2 , ny=0.
Onda metodom stacionarne perturbacije za trostruko degenerisano stanje, matrica 3x3, difrenciranje Hermitovih polinoma, sopstvene vrednosti matrice...

To petarm:
A koja ti te to teorema? Nema potrebe da se pozivas na neku teoremu to odmah sledi kad integralis sredingerovu jednacinu oko neke tacke. Mada kad nalazis grinovu funkciju za diff jednacinu sturm luvilovog tipa (tj. ona koja se moze predstaviti kao svojstveni problem autoadjugovanog operatora), se koristi kako izgleda wronskijan mada mislim da ta "teorema" nema nikakvo posebno ime.
to Bulada:
Nema potrebe da koristis Hermitove polinome i da se mucis da ih diferenciras, sa obzirom da znas kako izgledaju matricni elemeti operatora impulsa u svojstvenom bazisu. (a to kako izgleda dobijas kad napises operator impulsa preko operatora anhilacije i kreacije a za ove znas kako deluju na sv. bazis, ili alternativno resis lho u hajzenbergovoj slici to ti je samo matricna jednacina analogna 2. njutnovom zakonu i odmah dobijes ako se nevaram p[n,n-1]=p[n-1,n]=sqrt((n+1) h m omega/2) )
Inace cini mi se da ovo nisu zadaci za B smer vec verovatno za C.

pozdrav.

Kada kazem Sturm - Liuvilova teorema mislim na granicne uslove Sturm-Liuvilove jednacine.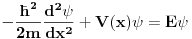



Hoces da kazes da ovo mozes da integralis za svako ? Uzmi ?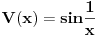

Recimo uzmimo ,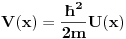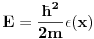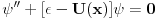



asimtotsko ponasanje resenja zavisi od znaka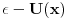

I na osnovu ovog znaka ja mogu reci nesto o spektru!

_{[Ovu poruku je menjao petarm dana 18.05.2008. u 14:07 GMT+1]}

Kakve veze ima neprekidnost talasne fje sa asimptotskim ponasanjem?
Pa naravno da mozes da integralis! (zapravo u tom primeru koji si naveo rezultat se izrazava preko specijalnih funkcija ci(x) ali to nije bitno bitno je samo da to tezi nuli kada granice integracije teze jedna drugoj) Cela poenta je da samo u slucaju kada imas delta fju za potencijal onda talasna fja mora da ima spic da bi izvod imao skok odonosno da bi drugi izvod dao delta fju koja ce kompenzovatio onu iz potencijala. Toliko.

pozdrav.

cekaj se definise ovako ?

Jeste i preko odgovarjuce smene mozes onaj tvoj primer da svedes na ci. Ali kao sto sam rekao nije u tome poenta.

pozdrav.