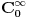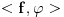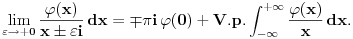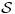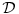[ petarm @ 09.04.2008. 18:54 ] @
|
[ petarm @ 09.04.2008. 19:02 ] @
A ako npr. definisem:
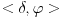 gde je gde je  iz iz  gde je gde je  prostor brzo opadajucih funkcija ova prica mi je laksa. Jer je vrlo lako naci fju koja je u beskonacnosti prostor brzo opadajucih funkcija ova prica mi je laksa. Jer je vrlo lako naci fju koja je u beskonacnosti  . Kao fizicaru ova prica mi nekako deluje realnije za rad? Ne znam doduse dal sam u pravu? Al to je moje misljenje! Ispravi me ako gresim. Moje pitanje je kada se koristi da je . Kao fizicaru ova prica mi nekako deluje realnije za rad? Ne znam doduse dal sam u pravu? Al to je moje misljenje! Ispravi me ako gresim. Moje pitanje je kada se koristi da je  u u  , a kada u , a kada u  ? ? I jos nesto da li u teoriji distribucija svojstvena funkcija nekog operatora moze biti  fja? fja? [ Nedeljko @ 11.04.2008. 12:07 ] @
Jedina elementarna funkcija i jedina analiticka funkcija u skupu
 je je  . Imas kod Boska Jovanovica . Imas kod Boska Jovanovica 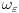 i i 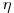 kao najjednostavnije i najvaznije osnovne funkcije koje se ne svode na nulu. kao najjednostavnije i najvaznije osnovne funkcije koje se ne svode na nulu.Konvergencija u skupu osnovnih funkcija se definise na sledeci nacin: Niz osnovnih funkcija konvergira ka nekoj osnovnoj funkciji ako je uniformno konvergentan ka njoj po svim mogucim izvodima i ako sve funkcije iz tog niza imaju zajednicki kompaktan nosac. Samo u tom slucaju ti se garantuje da dejstvo distribucije na clanovima tog niza konvergira ka dejstvu distribucije na granicnoj funkciji. Dakle, nema bezanje od kompaktnog nosaca. Dirakova distribucija je sopstveni vektor operatora mnozenja distribucije sa  . To je linearan operator definisan na svim distribucijama, jer je . To je linearan operator definisan na svim distribucijama, jer je 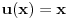 beskonacno diferencijabilna funkcija. beskonacno diferencijabilna funkcija.[Ovu poruku je menjao Nedeljko dana 11.04.2008. u 15:14 GMT+1] [Ovu poruku je menjao Nedeljko dana 11.04.2008. u 15:14 GMT+1] [ petarm @ 11.04.2008. 13:10 ] @
Citat: Nedeljko: Imas kod Boska Jovanovica [/tex]\omega_\varepsilon[/tx] i  kao najjednostavnije i najvaznije osnovne funkcije koje se ne svode na nulu. kao najjednostavnije i najvaznije osnovne funkcije koje se ne svode na nulu.Ajde molim te samo popravi ovo da bude lakse za citanje. Hvala na odgovoru. [ petarm @ 11.04.2008. 16:50 ] @
Nemam PDJ od Jovanovica trenutno kod sebe. Znaci 0 je primer funkcije u
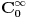 . Pa da funkcija . Pa da funkcija 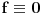 jeste svuda jednaka nuli van nekog konacnog intervala:) Za fiziku doduse apsolutno nebitan. Zato sto mi ne bi imalo smisla da talasna funkcija bude jeste svuda jednaka nuli van nekog konacnog intervala:) Za fiziku doduse apsolutno nebitan. Zato sto mi ne bi imalo smisla da talasna funkcija bude 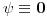 (cestica ne postoji). Znaci ovo 0 u (cestica ne postoji). Znaci ovo 0 u  mi ustvari predstavlja nosac? Odnosno kazuje da je kompaktan? mi ustvari predstavlja nosac? Odnosno kazuje da je kompaktan?Kako prokomentarisati ovaj primer? 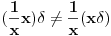 Da li je dovoljno reci da 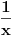 nije glatka? nije glatka?Citat: Nedeljko: Dirakova distribucija je sopstveni vektor operatora mnozenja distribucije sa  . To je linearan operator definisan na svim distribucijama, jer je . To je linearan operator definisan na svim distribucijama, jer je 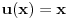 beskonacno diferencijabilna funkcija. beskonacno diferencijabilna funkcija.[Ovu poruku je menjao Nedeljko dana 11.04.2008. u 15:14 GMT+1] [Ovu poruku je menjao Nedeljko dana 11.04.2008. u 15:14 GMT+1] Gde se sve to desava?  mi je i linearan operator i svojstveni vektor? mi je i linearan operator i svojstveni vektor?[ Nedeljko @ 12.04.2008. 12:05 ] @
[ petarm @ 12.04.2008. 12:31 ] @
Citat: Ali postoje prostori gde 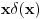 nije jednako nije jednako  Citat: Nedeljko: Funkcija 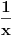 , kada je dodefinises u nuli, nije lokalno integrabilna, to jest, ne odgovara joj nijedna distribucija. Najpribliznija distribucija bi bila , kada je dodefinises u nuli, nije lokalno integrabilna, to jest, ne odgovara joj nijedna distribucija. Najpribliznija distribucija bi bila 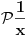 definisana sa definisana sa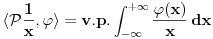 . Za nju vazi . Za nju vazi 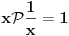 , odnosno , odnosno 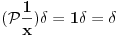 Sa druge strane je Sa druge strane je 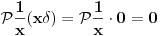 . .Neka je  linearan operator nad prostorom linearan operator nad prostorom 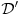 definisan sa definisan sa 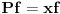 Tada je Tada je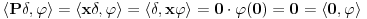 . .Drugim recima, 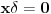 . .Moze li se odavde izvesti formula Sohockog? [ Nedeljko @ 13.04.2008. 12:05 ] @
Prvo pitanje ne razumem.
Što se drugog pitanja tiče, nigde nisam našao korektan dokaz formule Sohockog. Ono gowno u jednom redu koristi teoreme teorije harmonijskih funkcija (analitičke iz kompleksne analize) i primenjuje ih na funkcije koje nisu iz te klase. [ petarm @ 14.04.2008. 13:44 ] @
Citat: Nedeljko: Što se drugog pitanja tiče, nigde nisam našao korektan dokaz formule Sohockog. Ono gowno u jednom redu koristi teoreme teorije harmonijskih funkcija (analitičke iz kompleksne analize) i primenjuje ih na funkcije koje nisu iz te klase. Ne znam za taj dokaz u jednom redu? [ petarm @ 17.04.2008. 19:03 ] @
[ Nedeljko @ 17.04.2008. 20:24 ] @
Pomnoži nulu koliko god hoćeš brzorastućom funkcijom i dobićeš nulu, koja valjda u limesu daje nulu. Šta je tu čudno?
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|