Za mnoge operatore se jednostavno spominje domen i kodomen. Ali nisam video da to iko razmatra za anihilacioni i kreacioni operator?

Zapravo, ovi operatori deluju na prostoru kvadratno sumabilnih nizova.

bi trebalo da bude potprostor od . Ermitove funkcije su u a je u a to je potprostor od - brzo opadajuce funkcije. Te je i u . A dejstvom boze operatora mozes dobiti Ermitove funkcije ili ? A sve Ermitove fje su brzo opadajuce zbog faktora .

Ne znam odakle ti ovo, ali prostor druge kvantizacije je Fokov prostor i kreacioni i anihilacioni operatori deluju u njemu. Fokov prostor je reprezentovan prostorom kvadratno sumabilnih nizova.

Znam al ako je potprostor od , a ja dejstvom anihilacionih i kreacionih operatora ne mogu da izadjem iz ... Zar onda nije ova reprezentacija bolja?

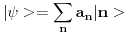
Ovo bi moglo da se nazove generalisanim Furijeovim razvojem! U slucaju diskretne reprezentacije bas generalisanim Furijeovim redom.

po definiciji



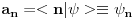
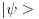
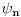
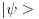
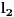
Dakle, diskretna reprezentacija stanja data je upravo skupom brojeva . Dakle u ovom slucaju imamo preslikavanje stanja na Hilbertov prostor kolona koji se oznacava sa . Ovaj prostor se kolko sam shvatio naziva Fokovim prostorom. Moje pitanje je sledece:
Kada imam Ermitove fje


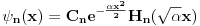
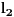
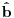
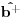
one su tzv. brzo opadajuce funkcije. Nalaze se u Svarcovom prostoru , zbog eksponencijalnog faktora. je svakako potprostor od . Zasto onda mi kazemo u fizici da operatori anihilacije i kreacije i deluju u Fokovom prostoru kad znamo mnogo bolje odredjenje njihovog domena?