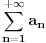
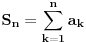
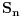
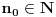
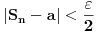
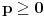
Neka je dat red i neka je niz njegovih parcijalnih suma. Ako je niz konvergentan ka nekom , onda za svako mozemo naci neko takvo da vazi za sve , pa ce za svako , biti .

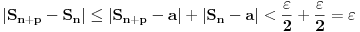
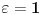
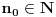
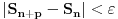
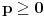
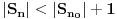
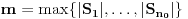
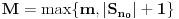
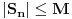
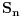
Neka je sada ispunjen Kosijev uslov. Stavljajuci da je za odgovarajuce takvog da je za sve i dobijamo da je za sve . Neka je i Tada je za sve , to jest, niz je ogranicen.

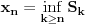
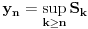
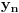
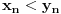
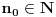
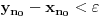
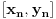
Neka je i Niz je neopadajuci, a niz nerastuci i vazi za svako . Iz Kosijevog uslova sledi da za svako postoji takvo da je zbog cega se presek niza umetnutih odsečaka svodi na neku tačku . Za svakako važi .

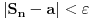
_{[Ovu poruku je menjao Nedeljko dana 10.04.2008. u 21:29 GMT+1]}

Hvala Nedeljko, izgleda da radi.
Hvala, pozdrav.