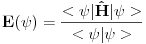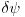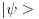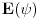Ovde treba da stoji

Ne razumem zašto ti je to problem. Varijacija stanja je proizvoljna tako da nema razloga zašto ne bi mogla da bude i na primer .

Problem mi je kad tu ubacim zar mi se tu ne menja i ?

Ne. je varijacija talasne funkcije. Ono što mi radimo sa izrazom je da variramo vektor stanja, tj. dodajemo mu mali pomeraj i zahtevamo da za svaki takav pomeraj vrednost leve strane ostane 0 (ovo će se desiti ako je stanje tačka ekstremuma gornjeg funkcionala).

U postavci gornje teoreme uzima se da je proizvoljan nenormiran vektor stanja iz . Postoji li neki nacin da se ista teorema dokaze za slucaj funkcionala ?

I zanima me jos nekoliko stvari u vezi sa ovim varijacionim metodom. Prv zasto se on koristi u kvantnoj hemiji? Odnosno zasto bas on? I drugo postoji li ikakva mogucnost da mi ocenimo gresku prilikom rada sa ovim metodom...?