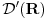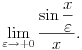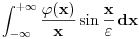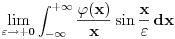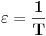[ Nedeljko @ 14.04.2008. 13:53 ] @
|
[ Nedeljko @ 15.04.2008. 14:00 ] @
[ Nedeljko @ 16.04.2008. 10:04 ] @
Ima li sanse da neko uradi ovaj zadatak, posto ja nisam uspeo sta god da sam pokusavao?
[ Fitopatolog @ 16.04.2008. 11:11 ] @
Nedeljko, šta ti ovde označava epsilon?
[ Nedeljko @ 16.04.2008. 11:28 ] @
[ Fitopatolog @ 16.04.2008. 15:25 ] @
Da nije možda sin(x/e) ustvari Si(x/e) - integralni sinus?
[ Fitopatolog @ 16.04.2008. 18:01 ] @
primenom parcijalne integracije, stavljajući
u=f(x) dv=sin(x/e) d(x/e) / (x/e) d je diferencijal dobija se rešenje f(x) D(x) Pi -f '(0) Pi D je delta funkcional, prvi član je nula (kada se uvrsti gornja i donja granica), tako da je konačan rezultat - f '(0) Pi ------------------------ p.s. Da li treba dokazati i da je integral ( sin(x/e) d(x/e) / (x/e)) od -beskonačno do x = D(x) kada e teži 0? [Ovu poruku je menjao Fitopatolog dana 16.04.2008. u 22:17 GMT+1] [Ovu poruku je menjao Fitopatolog dana 16.04.2008. u 22:19 GMT+1] [Ovu poruku je menjao Fitopatolog dana 16.04.2008. u 22:27 GMT+1] [ Fitopatolog @ 16.04.2008. 22:48 ] @
Prethodni račun nije dobar. Treba
sin(x/e) / x = D(x) Pi kada e teži 0, pa je rezultat f(0) Pi [Ovu poruku je menjao Fitopatolog dana 17.04.2008. u 09:06 GMT+1] [ Nedeljko @ 17.04.2008. 10:36 ] @
Hajde, ako ti nije tesko, napisi ceo racun, posto ideju sa tvojom prcijalnom integracijom nisam uspeo da kompletiram.
[ Fitopatolog @ 17.04.2008. 20:43 ] @
Huh, naterao si me da uzmem papir i olovku, rezultat je u attachmentu.
[ Nedeljko @ 18.04.2008. 11:05 ] @
Prihvatam da je
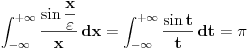 . Smena je . Smena je 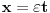 , kao i da je , kao i da je 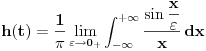 , gde je , gde je 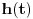 Hevisajdova funkcija. No, nejasna je jednakost Hevisajdova funkcija. No, nejasna je jednakost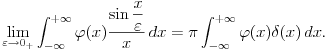 Ne prihvatam nikakvu Dirakovu "funkciju" 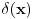 , jer u integralnom računu se dokazuje da takva funkjcija ne postoji. Prihvatam Dirakovu generalisanu funkciju, to jest Dirakovu distribuciju , jer u integralnom računu se dokazuje da takva funkjcija ne postoji. Prihvatam Dirakovu generalisanu funkciju, to jest Dirakovu distribuciju  , ali se ona ne može naći pod integrealom. Umesto toga treba koristiti dejstvo distribucije na test funkciju. No, čak i kada se na taj način gornja jednakost prevede, ona postaje jednakost , ali se ona ne može naći pod integrealom. Umesto toga treba koristiti dejstvo distribucije na test funkciju. No, čak i kada se na taj način gornja jednakost prevede, ona postaje jednakost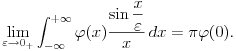 koja mi takođe nije jasna. Drugo rešenje nije prihvatljivo, jer iz 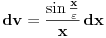 nikako ne sledi nikako ne sledi 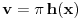 jer ne važi jer ne važi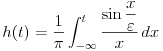 već 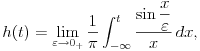 a to nije isto. Takođe limesom se ne može ući pod integral u opštem slučaju, već treba proveriti da li su ispunjeni uslovi pod kojima se takav prelaz može napraviti. [ Nedeljko @ 18.04.2008. 14:02 ] @
Uspeo sam da uradim zadatak. Prvo, parcijalnom integracijom se dobija da je
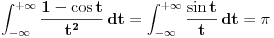 . Smenom . Smenom 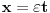 dobija se da je dobija se da je 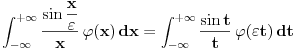 . Parcijalnom integracijom ( . Parcijalnom integracijom (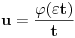 , , 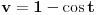 to je dalje jednako to je dalje jednako 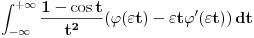 . Funkcija . Funkcija 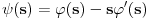 je ogranicena kao neprekidna funkcija sa kompaktnim nosacem (koji je isti kao i za je ogranicena kao neprekidna funkcija sa kompaktnim nosacem (koji je isti kao i za 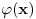 . Stoga postoji . Stoga postoji 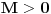 za koje je za koje je 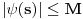 . No, odatle je . No, odatle je 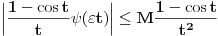 , pa posto je , pa posto je 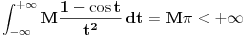 po Lebegovom stavu o dominantnoj konvergenciji mozemo uci limesom pod integral, pa je konacno po Lebegovom stavu o dominantnoj konvergenciji mozemo uci limesom pod integral, pa je konacno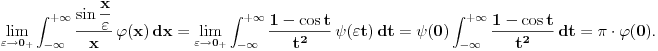 Znaci, 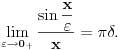 [ petarm @ 18.04.2008. 20:14 ] @
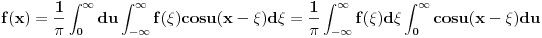 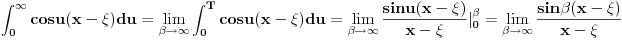 Vratim ovo u gornji izraz i dobijem 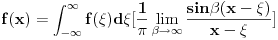 Odavde se vidi da izraz u srednjoj zagradi anulira integraciju po 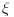 i integracionu promenljivu zamenjuje slobodnom promenljivom i integracionu promenljivu zamenjuje slobodnom promenljivom  . A ovu osobinu ima . A ovu osobinu ima  funkcija. Pa je prema tome funkcija. Pa je prema tome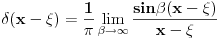 Ovako to rade fizicari [ Fitopatolog @ 18.04.2008. 20:54 ] @
Da pokušamo da napravimo reda u terminologiji:
- funkcional je preslikavanje skupa funkcija A na skup brojeva - <g,f> je takođe funkcional koji uređenu dvojku funkcija (g,f) iz proizvoda skupova funkcija A X A preslikava na skup brojeva. U našem slučaju funkcional je INTEGRAL. - specijalna klasa funkcija D (D je podskup A) ima važnu osobinu da je (i dalje zadržavamo kao funkcional integral) <d,f> = f(0) ; d pripada D abs(d) = 0 za abs(x) > e, e teži 0 bilo kog predstavnika klase D zovemo delta-funkcija. [ Fitopatolog @ 18.04.2008. 21:34 ] @
delta f-ja se (između ostalih sličnih načina) može dobiti i kao
d(x) = k*exp(-k*x) za x>=0 i k teži 0+ [ Nedeljko @ 18.04.2008. 22:28 ] @
@petarm
Za 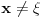 integral integral 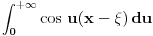 divergira. divergira.@Fitopatolog Pojam integrala, onakvog kakav je danas u upotrebi, definisao je Anri Lebeg. U Lebegovoj teoriji integracije lako se dokazuje sledeća teorema: Ne postoji nijedna funkcija  takva da za svako takva da za svako 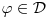 važi važi 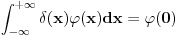 . .Distribucija je svaki linearni funkcional  koji slika skup koji slika skup 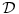 u skup realnih brojeva takav da važi u skup realnih brojeva takav da važi 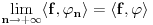 kad god sve test funkcije kad god sve test funkcije 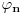 imaju zajednički kompaktan nosač i imaju zajednički kompaktan nosač i 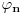 teži uniformno ka teži uniformno ka  po svim izvodima. po svim izvodima.Lokalno integrabilnoj funkciji  pridružuje se distribucija koja se obeležava istim simbolom, definisana kao pridružuje se distribucija koja se obeležava istim simbolom, definisana kao 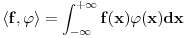 . No, to je samo jedan od načina da se zada distribucija i takve distribucije (zadate integralom) zovemo regularnim. . No, to je samo jedan od načina da se zada distribucija i takve distribucije (zadate integralom) zovemo regularnim.Dirakova distribucija se definiše sa 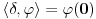 i ona nije regularna (u tom se slučaju kaže da je singularna), to jest, ne može se zadati integralom. Upravo o tome govori prethodna teorema. i ona nije regularna (u tom se slučaju kaže da je singularna), to jest, ne može se zadati integralom. Upravo o tome govori prethodna teorema.[ petarm @ 18.04.2008. 23:22 ] @
Citat: Nedeljko: Lokalno integrabilnoj funkciji  pridružuje se distribucija koja se obeležava istim simbolom, definisana kao pridružuje se distribucija koja se obeležava istim simbolom, definisana kao 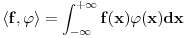 . No, to je samo jedan od načina da se zada distribucija i takve distribucije (zadate integralom) zovemo regularnim. . No, to je samo jedan od načina da se zada distribucija i takve distribucije (zadate integralom) zovemo regularnim.Dirakova distribucija se definiše sa 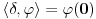 i ona nije regularna (u tom se slučaju kaže da je singularna), to jest, ne može se zadati integralom. Upravo o tome govori prethodna teorema. i ona nije regularna (u tom se slučaju kaže da je singularna), to jest, ne može se zadati integralom. Upravo o tome govori prethodna teorema.Da li je Hevisajdova fja regularna distribucija? Mozes li to prokomentarisati na ovom primeru? Citat: Nedeljko:@Fitopatolog Pojam integrala, onakvog kakav je danas u upotrebi, definisao je Anri Lebeg. U Lebegovoj teoriji integracije lako se dokazuje sledeća teorema: Ne postoji nijedna funkcija  takva da za svako takva da za svako 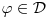 važi važi 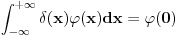 . .Mozes li ovo pokazati? Citat: Mozes li objasniti zasto ja radeci "pogresno" dobijam dobar rezultat? [ Fitopatolog @ 19.04.2008. 08:31 ] @
Citat: Nedeljko: @petarm Pojam integrala, onakvog kakav je danas u upotrebi, definisao je Anri Lebeg. U Lebegovoj teoriji integracije lako se dokazuje sledeća teorema: Ne postoji nijedna funkcija  takva da za svako takva da za svako 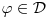 važi važi 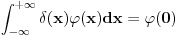 . . Dobro, da li d(x,e), e teži 0 (iz naslova zadatka ili iz mog pretposlednjeg posta), možemo smatrati funkcijom? Takođe, da li postoji bar jedna f-ja d(x) tako da gornji integral važi bar za NEKE funkcije fi? [Ovu poruku je menjao Fitopatolog dana 19.04.2008. u 10:38 GMT+1] [ Nedeljko @ 19.04.2008. 10:33 ] @
Hevisajdova funkcija je neprekidna u svim tackama osim u jednoj, u cijoj je okolini ogranicena, iz cega sledi da je lokalno integrabilna. Odatle sledi da ona indujuje je jednu regularnu distribuciju.
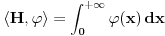 . .Citat: petarm: Mozes li ovo pokazati? Neka je 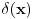 trazena funkcija i neka je segnemt trazena funkcija i neka je segnemt 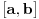 takav da ne sadrzi nulu. Neka je takav da ne sadrzi nulu. Neka je 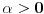 i i 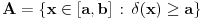 . Skup . Skup  je merljiv, jer je funkcija je merljiv, jer je funkcija  merljiva kao lokalno integrabilna. Stoga, za svako merljiva kao lokalno integrabilna. Stoga, za svako  postoji zatvoren skup postoji zatvoren skup 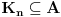 takav da je takav da je 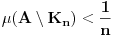 . Taj skup je kao zatvoren i ogranicen kompaktan. Takodje, postoji otvoren skup . Taj skup je kao zatvoren i ogranicen kompaktan. Takodje, postoji otvoren skup 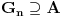 takav da je takav da je 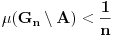 . Bez umanjenja opstosti mozemo jos pretpostaviti da je . Bez umanjenja opstosti mozemo jos pretpostaviti da je 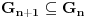 , , 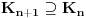 i da i da 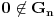 . U knjizi "Parcijalne jednacine" Boska Jovanovica se moze naci primer funkcije . U knjizi "Parcijalne jednacine" Boska Jovanovica se moze naci primer funkcije 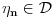 takve da je takve da je 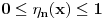 , , 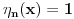 za za 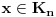 i i 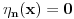 za za 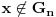 . .Posto je  lokalno integrabilna funkcija, vazi lokalno integrabilna funkcija, vazi 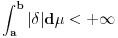 , pa posto je , pa posto je 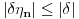 i i 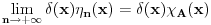 skoro svuda, gde je skoro svuda, gde je 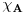 funkcija koja je jednaka jedinici u tackama skupa funkcija koja je jednaka jedinici u tackama skupa  ,a u ostalim tackama je jednaka nuli, Lebegov stav o dominantnoj konvergenciji se moze primeniti, pa je ,a u ostalim tackama je jednaka nuli, Lebegov stav o dominantnoj konvergenciji se moze primeniti, pa je 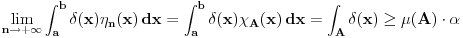 . .Sa druge strane je 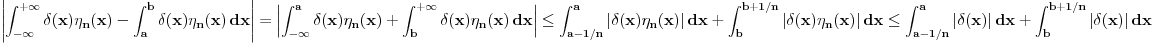 , ,sto je zbog lokalne integrabilnosti funkcije  za dovoljno veliko za dovoljno veliko  manje od zadatog manje od zadatog  . No, zajedno sa . No, zajedno sa 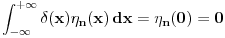 odatle sledi da je odatle sledi da je 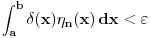 za dovoljno veliko za dovoljno veliko  , pa je , pa je 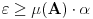 . Posto je . Posto je  proizvoljno, odatle sledi (zbog proizvoljno, odatle sledi (zbog 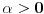 ) da je ) da je 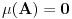 . .Znaci, za svako  vazi da je vazi da je 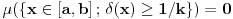 , pa je i skup , pa je i skup 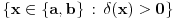 mere nula kao prebrojiva unija skupova mere nula. No, segment mere nula kao prebrojiva unija skupova mere nula. No, segment 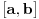 je bio proizvoljan segment koji ne sadrzi nulu, pa posto je je bio proizvoljan segment koji ne sadrzi nulu, pa posto je 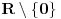 prebrojiva unija takvih intervala, bice prebrojiva unija takvih intervala, bice 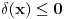 skoro svuda na skoro svuda na 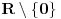 , pa samim tim i na skoro svuda na , pa samim tim i na skoro svuda na  jer je jednoclan skup mere nula. Na slican nacin se moze dokazati i da je jer je jednoclan skup mere nula. Na slican nacin se moze dokazati i da je 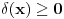 skoro svuda, odakle je skoro svuda, odakle je 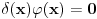 skoro svuda za ma kakvu funkciju skoro svuda za ma kakvu funkciju  odakle je odakle je 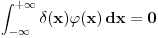 suprotno polaznoj pretpostavci. suprotno polaznoj pretpostavci.[ Nedeljko @ 19.04.2008. 11:00 ] @
Citat: petarm: Mozes li objasniti zasto ja radeci "pogresno" dobijam dobar rezultat? Prvo, matematika ti garantuje samo da ako radis dobro, da moras dobiti dobar rezultat. Ako radis pogresno, nema nikakvih garancija ni da ce rezultat biti dobar, ni da ce biti pogresan. Seti se istinitosne tablice implikacije. Iz tacnog sledi samo tacno, a iz netacnog slede i tacno i netacno. Drugo, tvoja ideja jeste dobra, i moze se "doterati" u formalno korektne vode. Zato i ne iznenadjuje cinjenica da si dobio tacan rezultat. Citat: Fitopatolog: Dobro, da li d(x,e), e teži 0 (iz naslova zadatka ili iz mog pretposlednjeg posta), možemo smatrati funkcijom? Takođe, da li postoji bar jedna f-ja d(x) tako da gornji integral važi bar za NEKE funkcije fi? Rekao bih da kod tvojeg d(x,k) treba k da ide u beskonacnost. No, nema veze. Na taj nacin dobijas limes u klasicnoj analizi koji je nula svuda van nule, pa kada se pomnozen bilo kojom funkcijom prointegrali daje nulu. Ako se limes radi u prostoru distribucija, granicna vrednost je Dirakova distribucija. Za bilo koji konacan broj funkcija  postoji funkcija postoji funkcija  takva da je takva da je 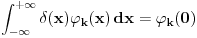 . .[ petarm @ 19.04.2008. 11:37 ] @
Nedeljko:
Drugo, tvoja ideja jeste dobra, i moze se "doterati" u formalno korektne vode. Zato i ne iznenadjuje cinjenica da si dobio tacan rezultat. Jel mozes da pokazes kako bi se ta ideja mogla korektno sprovesti? [ Fitopatolog @ 19.04.2008. 12:02 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|