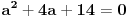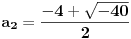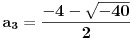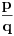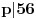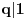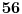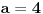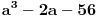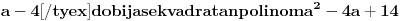[ misham @ 15.04.2008. 06:22 ] @
| 1.kako resiti jednacinu : a^3 -2a-56=0; 2.odrditi m,n elementi skupa N;tako da zbir brojeva izmedju njih bude 1000; 3.U krug je upisan sedmougao, sa tri ugla od 120 stepeni.dokazati da ima bar 2 stranice jednake. -treci zadatak sam podelio na dva slucaja 1.kada su dva susedna ugla 120(ovaj slucaj se lako dokazuje) 2.kada je svaki drugi 120, i ostanu dva susedna ugla o kojima ne znamo nista. u ovom slucaju dodjem do kontradikcije, povucem poluprecnike iz svakog temena, i onda dobijem da su dva ugla u jednom trouglu od 90 stepeni, a jedan od 0. hvala puno ako iko pomogne. |