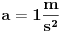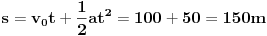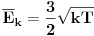[ Nedeljko @ 25.04.2008. 17:42 ] @
|
[ McKracken @ 25.04.2008. 21:14 ] @
Citat: U matematici ne postoje merne jedinice, pa ipak nikome ne pada na pamet da sabira babe i žabe, (dužine i zapremine i tome slično). U fizici ima pokusaja da se sabiraju babe i zabe. [ Bojan Basic @ 25.04.2008. 21:20 ] @
Ima pokušaja, ali oni koji znaju šta rade (verujem da Nedeljko misli na takve) ne bi sabirali babe i žabe bez obzira na to da li postoje merne jedinice ili ne. Onima koji pak ne znaju ne pomažu ni merne jedinice ni druge (uslovno rečeno) olakšice.
[ Predrag Supurovic @ 25.04.2008. 22:15 ] @
Citat: Nedeljko: Kada kažem da je dijagonala mog monitora iznosi 0.432 m, ja sam zapravo izrazio odnos dveju dužina: dijagonale mog monitora i etalona metra. Taj iskaz se u suštini ne razlikuje od iskaza: dijagonala mog monitora je 3 puta kraća od visine mog prozora. Merne jedinice su uvedene zato da bi mogao nekome da kazes kolika je dijagonala tvog monitora ako on ne zna kolike su dimenzije tvoj prozora. Drugim recima, ako prodajes taj monitor i neko se interesuje da li je monitor dovoljno mali da stane tamo gde bi on hteo da ga umetne, nista mu ne bi znacilo sto je dijagonala tog monitora 3 puta kraca od dijagonale tvog prozora, jer njega interesuje da li monitor moze da stane na policu koju on ima. Zato je uveden metar jer svako zna koliki je metar. [ Bojan Basic @ 26.04.2008. 00:19 ] @
Predraže, svi smo svesni da se moramo dogovoriti koliko će iznositi jedinična dužina i da se ravnamo po tome. Pitanje je (bar ga ja tako doživljavam) zašto moramo lepiti to „m“ uz svaku dužinu koju iskažemo. Ako nekom kažeš da je dužina dijagonale tvog monitora jednaka 0,432, jasno je da si izrazio odnos s etalonom dužine, nećeš izražavati dužinu dijagonale monitora u Celzijusovim stepenima.
Pokušaću odmah da odgovorim na dalja pitanja koja bi mogla uslediti. Neko bi mogao reći: „A šta ako ja sve merim u inčima a ne u metrima, kako treća osoba da zna na koje jedinice ja mislim?“ Inč (po naški: palac ili col) nije etalon, etalon je metar (tj. dužina onoga što danas nazivamo metar), i jedinice bi se ipak morale zapisivati ako su nestandardne, dok bi se standardna podrazumevala kad ništa ne piše (ovakav slučaj već postoji u matematici, i funkcioniše bez ikakvih problema: neko može da kaže kako je veličina određenog ugla jednaka  , a drugi za taj isti ugao može reći da mu je veličina jednaka , a drugi za taj isti ugao može reći da mu je veličina jednaka 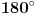 ; dakle, ovaj što bi da izražava vrednost ugla u stepenima, mora da stavi njihov znak nakon brojčane vrednosti, dok onaj ko izražava u radijanima to ne mora da naglašava posebno — i ovo ne izaziva baš nikakve nejasnoće među matematičarima). ; dakle, ovaj što bi da izražava vrednost ugla u stepenima, mora da stavi njihov znak nakon brojčane vrednosti, dok onaj ko izražava u radijanima to ne mora da naglašava posebno — i ovo ne izaziva baš nikakve nejasnoće među matematičarima).Neko drugi bi se mogao nadovezati: „Kako ćemo ubediti ceo svet da baš metar bude etalon? Uzmimo Engleze za primer, oni uglavnom mere u inčima, ko bi njih naterao da prihvate metar kao jedini zvaničan?“ Ovo pitanje nema baš mnogo smisla, jer metar već jeste zvaničan prema SI-sistemu, koji je prihvaćen po celom svetu. [ Fitopatolog @ 26.04.2008. 03:34 ] @
Merne jedinice su zgodne za proveru formula, npr. ako iz v=s/t (brzina=put/vreme) pogrešno zaključiš da je s=v/t, dobićeš da se s izražava u m/s**2 i odmah znaš da nešto ne štima.
[ petarm @ 26.04.2008. 08:11 ] @
Da jeste korisno da znas dal ti dimenzija odgovara! Npr. u fizici se dosta cesto radi u tzv. Dirakovoj notaciji a onda kad su nam potrebne brojke prelazimo u npr. koordinatnu reprezentaciju. Ono sto je bitno a na sta treba paziti u fizici je sledece.
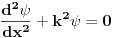 Matematicar ce ovo pogledati i reci ce. Super evo mi diferencijalna jednacina. A strogo da bi ovo bila diferencijalna jednacina mora se preci na bezdimenzione promenljive jer je  npr. duzina. npr. duzina. 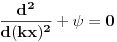 A ovo sto je uzeto kao sto je uzeto. Npr. zasto metar, sekund i tako dalje, ima veze sa nekim eksperimentalnim vrednostima. Ali mislim da je sustinska stvar u ovome sto je vec naglaseno. To je etalon pomocu kojeg mozes svakome izraziti svoj rezultat, a da te on ne zapita koliko je to. Slicna prica bila bi u sledecem sto ja recimo ne bih pisao integral ovako  ? ? Matematicarima naravno neke stvari nisu bitne. Uzmite neku fiziku koju su pisali matematicari. Sve brojne konstante oni pisu sa  i bas ih briga jel to i bas ih briga jel to  il il 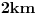 il je to mozda duzina puta koju Nedeljko dnevno prepesaci! il je to mozda duzina puta koju Nedeljko dnevno prepesaci![ petarm @ 26.04.2008. 09:02 ] @
Inace za duzinu i nije takav problem. Ali ajde npr. snagu. Daj mi primer kako ces izrazavati snagu. U kojim jedinicima? I u tvom vidjenju stvari javice se problem sa fizickim velicinama koje nemaju jedinicu.
Citat: Nedeljko: Raspravljao sam se sa kolegama na poslu i nikako da ih ubedim da ne postoji nikakva esencijalna potreba za mernim jeinicama, već eventualno praktična, pa me zanima kako drugi razmišljaju o tome. Kada kažem da je dijagonala mog monitora iznosi 0.432 m, ja sam zapravo izrazio odnos dveju dužina: dijagonale mog monitora i etalona metra. Taj iskaz se u suštini ne razlikuje od iskaza: dijagonala mog monitora je 3 puta kraća od visine mog prozora. Jedino što zaista mogu izraziti je odnos između dve dužine, bez obzira da li je imenilac neki dogovoreni etalon ili neka druga dužina, a da bih izrazio odnos između dveju dužina, ne treba mi nikakav sistem mernih jedinica. Rezultat je čist realan broj bez dimenzije, koji ne zavisi od izbora mernih jedinica. Inace za duzinu i nije takav problem. Ali ajde npr. snagu. Daj mi primer kako ces izrazavati snagu. U kojim jedinicima? I u tvom vidjenju stvari javice se problem sa fizickim velicinama koje nemaju jedinicu. Citat: Nedeljko: Nikako da ubedim kolege da je mol jedinica koliko i radijan To jednostavno nije tako. [ Predrag Supurovic @ 26.04.2008. 09:16 ] @
@Bojan Basic
Jedinice se pisu uz brojeve zato sto pored osnovne jedinice postoje vece i manje jedinice. Vrlo cesto u praksi se ne korsiti osnovna merna jedinica nego neka veca ili manja. Ako uzmemo da je etalonza duzinu metar i ne pisemo ga, to znaci da i dimenziju od 2 mm moramo da izrazimo u u metrima, ili jos gore, dimenzije u mikrometrima... Ili jos jedana primer, nama blizi.. svako ko zalazi u podforume o umrezavanju moze na svakom koraku da vidi kako se ljudi zbunjuju oko jedinica za izrazavanje brzine protoka iako se te jedinice obavezno pisu. Sta bi tek bilo da ih ne pisemo? Ili, kako bi izgledalo da sve memrijske kapacitet izrazavamo neimenovanim brojevima koji oznacavaju bajtove? Sam potreba da se korsite manje i vece jedinice namece potrebu da se one kao takve moraju oznaciti a ako ne bi smo oznacavali i samuosnovnu jedinicu to bi lako moglo da dovede do zabune. Recimo, ko je ikada gledao kako gradjevinari obelezavaju dimenzije, primetio je da oni metar ne obelezavaju sa m vec sa m1, jer tako jos vise izbegavaju mogucnost zabune. Na kraju krajeva, jedinice koristimo zato sto je u prirodi ljudskog nacina razmsiljanja i jezika da sve ima ime. Ljudi su davali imena mernim jedinicama mnogo pre nego sto su postojali bilo kakvi standardi. Da li je to bio prst, pedalj, hvat, lakat, stopa, korak ili nesto drugo, uvek je imalo ime. [ kukiii @ 26.04.2008. 09:20 ] @
Citat: Jedino što zaista mogu izraziti je odnos između dve dužine, bez obzira da li je imenilac neki dogovoreni etalon ili neka druga dužina, a da bih izrazio odnos između dveju dužina, ne treba mi nikakav sistem mernih jedinica. Rezultat je čist realan broj bez dimenzije, koji ne zavisi od izbora mernih jedinica. Da bi znao da li su brojevi koje upoređuješ dužine, potrebne su tu jedinice. Čini mi se da ti kažes nisu nam potrebne jedinice a ustvari mislis da nije potrebno pisati iste. Sad, nekom je lakse da pise, a nekom da pamti. [ petarm @ 26.04.2008. 11:27 ] @
U nekim racunima debilno je stalno vuci jedinice i to se i ne radi. Ali zato sve pre toga prebacimo u osnovne jedinice SI sistema.
[ cicika @ 26.04.2008. 13:17 ] @
Citat: U nekim racunima debilno je stalno vuci jedinice Ne "vuku" se sve dok pišeš u opštim brojevima odnosno oznakama veličina. Onog trenutka kada izračunaš brojni rezultat moraš da staviš jedinicu jer inače taj brojni rezultat ne znači bukvalno ništa. [ petarm @ 26.04.2008. 13:50 ] @
[ Nedeljko @ 26.04.2008. 14:23 ] @
Da formulišem svoj stav ovako:
Ako u definicijama neke teorije imam začarani krug, onda sa tim definicijama nešto nije u redu i tu nešto treba menjati. Ako nemam začarani krug, onda mogu uočiti da se u tim definicijama pojavljuju neki pojmovi koji nemaju definiciju. To su takozvani osnovni ili polazni ili nedefinisani pojmovi. Sa druge strane, primetićemo da su svi ostali pojmovi koji figurišu u tim definicijama (bilo u definiensu ili u definiendumu) definisani, direktno ili indirektno, preko tih polaznih pojmova. Oni se zovu izvedeni ili definisani pojmovi. Dakle, svaka teorija ima svoje polazne i izvedene pojmove. Da bi definicija bila korektna, pred nju se postavljaju dva zahteva: da se može eliminisati iz svakog iskaza i da se može eliminisati iz dokaza bilo kog tvrđenja čiji iskaz ne koristi pojam uveden tom definicijom. Dakle, ako su definicije korektne, iz svih iskaza se mogu eliminisati svi izvedeni pojmovi i dobiće se ekvivalentna formulacija iskaza u kome učestvuju samo osnovni pojmovi. Takođe, sve teoreme će nakon eliminacije svih definicija moći da se dokažu i bez upotrebe definicija. Naravno, sve uz pretpostavku da su definicije korektne. E, sad ide ono glavno. Merne jedinice imaju svoje definicije, to jest, ne spadaju u osnovne, već u izvedene pojmove. Na stranici http://en.wikipedia.org/wiki/International_System_of_Units možete naći linkove prema definicijama svih sedam osnovnih jedinica SI sistema. Dakle, pošto spadaju u izvedene pojmove, uvek se mogu eliminisati, to jest, sve što može sa njima, može i bez njih. Ne kažem da su merne jedinice potpuno beskorisne. Korisne su koliko su i definicije korisne, ali ne igraju nikakvu esencijalnu, već samo pomoćnu ulogu, baš kao i definicije. [ mulaz @ 26.04.2008. 15:07 ] @
Kako cez bez jedinica da pokazes razliku izmedju:
-5VA -4W -3VAr ? [ Bojan Basic @ 26.04.2008. 15:16 ] @
Citat: Predrag Supurovic: Ako uzmemo da je etalonza duzinu metar i ne pisemo ga, to znaci da i dimenziju od 2 mm moramo da izrazimo u u metrima, ili jos gore, dimenzije u mikrometrima... Ne vidim da je „2 mm“ išta značajno kraće od „2·10-3“, ali svakako si promašio temu. Nedeljko je u prvoj poruci izneo tezu: Citat: a ovo što ti pričaš (da ćeš nekom možda uštedeti dva poteza olovkom) nikako se ne može svrstati u ovo „crveno“, eventualno u „plavo“ — što nije tema ovde. [ Nedeljko @ 26.04.2008. 16:05 ] @
Citat: Predrag Supurovic: Merne jedinice su uvedene zato da bi mogao nekome da kazes kolika je dijagonala tvog monitora ako on ne zna kolike su dimenzije tvoj prozora. Drugim recima, ako prodajes taj monitor i neko se interesuje da li je monitor dovoljno mali da stane tamo gde bi on hteo da ga umetne, nista mu ne bi znacilo sto je dijagonala tog monitora 3 puta kraca od dijagonale tvog prozora, jer njega interesuje da li monitor moze da stane na policu koju on ima. Zato je uveden metar jer svako zna koliki je metar. Mogao sam da izrazim dijagonalu i u talasnim dužinama nekog zračenja kao što je ono preko koga se definiše sekunda, pa ne bih imao potrebe da mu saopštavam koliki je metar, već bi on mogao i sam da izmeri talasnu dužinu tog zračenja i znao bi da li monitor može da mu stane na policu. Citat: petarm: To jednostavno nije tako. Zašto mol nije jedinica koliko i radijan? To je samo Avogadrov broj, bez dimenzije, kao što je kelvin izraziv preko metra i sekunde. Citat: cicika: Onog trenutka kada izračunaš brojni rezultat moraš da staviš jedinicu jer inače taj brojni rezultat ne znači bukvalno ništa. Zašto rezultat "dužina moje sobe je četiri puta veća od visine mog prozora" bez jedinica ne znači ništa? Moj stav je da esencijalno, samo odnose dužina i možeš da izraziš, a ne neku dužinu u apsolutnom smislu, bez poređenja sa nekom drugom dužinom. Citat: Sadržaj fizičke teorije čine njena predviđanja rezultata eksperimenata. Formuliši konkretan eksperiment (ili fizičko stanje) i vlo dobro će se znati šta je električni napon, šta energija, šta dužina itd. Van konteksta, veličine ne znače skoro ništa. [ petarm @ 26.04.2008. 16:19 ] @
@Nedeljko
Mogao sam da izrazim dijagonalu i u talasnim dužinama nekog zračenja kao što je ono preko koga se definiše sekunda, pa ne bih imao potrebe da mu saopštavam koliki je metar, već bi on mogao i sam da izmeri talasnu dužinu tog zračenja i znao bi da li monitor može da mu stane na policu. Sto se tice ovoga sa talasnim duzinama. 14.10.1960. godine odlukom Internacionalne konferencije utvrdjeno je da je 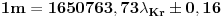 gde je 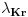 talasna duzina narandzaste linije u spektru izotopa talasna duzina narandzaste linije u spektru izotopa 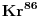 . .Naravno ovo je dobijeno opticki preciznim merenjima. Moras da shvatis da se u fizici mnogo meri i gleda se neko preklapanje izmedju teorijskih i eksperimentalnih rezultata. I zato su i uvedeni odredjeni etaloni. @Nedeljko Zašto mol nije jedinica koliko i radijan? To je samo Avogadrov broj, bez dimenzije, kao što je kelvin izraziv preko metra i sekunde. Mol nije samo Avogadrov broj! [ mulaz @ 26.04.2008. 16:37 ] @
Citat: Nedeljko: Sadržaj fizičke teorije čine njena predviđanja rezultata eksperimenata. Formuliši konkretan eksperiment (ili fizičko stanje) i vlo dobro će se znati šta je električni napon, šta energija, šta dužina itd. Van konteksta, veličine ne znače skoro ništa. onaj moj primer (W VAr i VA) svi oznacavaju razlicitu 'vrstu' snage. Ako kazes da je snaga nekog generatora 500W, 500VA, ili 500VAr su to potpuno razlicite stvari. [ Mikky @ 26.04.2008. 16:55 ] @
Mislim da vecina ucesnika teme ne shvata sta Nedeljko zapravo zeli da kaze svojim striktnim matematicarskim nacinom izrazavanja :). Nije tema o tome da li su merne jedinice prakticne i kako se definisu vec da li mozemo da zivimo bez njih. Kratak odgovor bi bio: mozemo.
Malo duzi: mozemo ali ne bi nam zivot bio mnogo tezi. Analogno pitanje: da li nam je neophodan automobil da bi otisli na more. Kratak odgovor: nije. Duzi odgovor: nije ali bi nam zivot bio mnogo tezi. Prvo se treba zapaziti da su merne jedinice usko povezane sa merenjem a merenje predstavlja u najopstijem slucaju uporedjivanje velicina. Dakle jedinice nisu neophodne, one predstavljaju implementaciju apstraktnijeg pojma "uporedjivanje velicina" pa s' toga nisu esencijalne same po sebi. Sa druge strane sam koncept "uporedjivanje velicina" je neophodnost bez koje mislim da ne bi mogli da razvijemo fiziku u opste. Tako da sa te strane "uporedjivanje velicina" jeste neophodnost dok nacin kako cemo to da komuniciramo medjusobno (radi resavanja konkretnih problema) nije jedinstven (npr preko SI standarda jedinica) pa samim tim ni neophodan. mulaz, te jedinice predstavljaju jednu te istu velicinu - snagu. Ali zbog prakticnih (inzinjerskih) razloga je bilo potrebno znati koliko snage u kolu ide na koristan rad a koliko na stvaranje el.mag polja od kojih potrosac nema koristi. To nije neophodnost ali nas skracuje muka. To je isto kao kad bih ja gurao neka kolica i merio posebno rad koji utrosim na savladavanje sile trenja i nazvao ga reaktivan rad sa jedinicom N*m (njutn puta metar) a rad koji utrosim na pomeranje mase kolica nazvao aktivan rad sa jedinicom J (dzul). [Ovu poruku je menjao Mikky dana 26.04.2008. u 18:07 GMT+1] [ petarm @ 26.04.2008. 20:26 ] @
Voleo bih da procitate uvod iz Mehanike fluida profesora Stanoja Stojanovica.
UVOD U mehanici, makroskopsko telo pod dejstvom sila koje na njega deluju, u opštem slučaju, vrši složeno kretanje. Ovo složeno kretanje se u osnovi može razložiti na translatorno pomeranje tela, njegovu rotaciju oko trenutne ose i deformaciju. Često nas u pojedinim slučajevima ne interesuje ovakva opšta slika kretanja, već pojedini oblici ovog kretanja. Tako, za opisivanje pojava vezanih za translatorno kretanje uvodi se model materijalne tačke kojim se zamenjuje realno telo. Ili, za opisivanje pojava vezanih za rotaciono kretnje, realno telo se zamenjuje modelom apsolutno krutog tela. Međutim, za opisivanje pojava koje su posledica deformacije tela, nijedan od gornja dva modela nije dobar, već se mora uvesti treći model - model kontinuuma. Kod deformabilnih tela rastojanja između molekula se menjaju pod dejstvom sila koje na njega dejstvuju. Pošto telo sadrži veoma veliki broj molekula (red veličine Avogadrovog broja 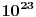 ), jasno je da ovakvi sistemi (tela) imaju vrlo veliki broj stepeni slobode. Čini se na prvi pogled da bi mehaniku ovakvih sistema mogli razvijati na bazi predstave o makroskopskom telu kao klasično-mehaničkom sistemu čestica. Međutim, u ovakvom prilazu postoji izvestan broj vrlo ozbiljnih problema. Prvi je, iako su sile među atomima elektromagnetne prirode, one su često nepoznate (ne zna se njihov analitički oblik). Drugi je, zbog veoma velikog broja atoma, broj dinamičkih jednačina je, takođe, veoma velik ( ), jasno je da ovakvi sistemi (tela) imaju vrlo veliki broj stepeni slobode. Čini se na prvi pogled da bi mehaniku ovakvih sistema mogli razvijati na bazi predstave o makroskopskom telu kao klasično-mehaničkom sistemu čestica. Međutim, u ovakvom prilazu postoji izvestan broj vrlo ozbiljnih problema. Prvi je, iako su sile među atomima elektromagnetne prirode, one su često nepoznate (ne zna se njihov analitički oblik). Drugi je, zbog veoma velikog broja atoma, broj dinamičkih jednačina je, takođe, veoma velik ( 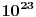 ), što, praktično, predstavlja nerešiv problem. Treći, čak i da možemo integraliti ovoliko veliki broj dinamičkih jednačina, određivanje integracionih konstanti, zbog principijelne nemogućnosti da istovremeno i tačno znamo položaj i brzinu svakog atoma u nekom početnom trenutku (početni uslovi), je nemoguće izvršiti. Međutim, čak i kada bismo mogli da nađemo konačne jednačine kretanja svih molekula, od ovakve detaljne slike ne bismo imali praktično nikakve koristi, jer bi prelaz na makroskopsku sliku zahtevao isuviše mnogo vremena. Prema tome, ovakav klasično-mehanički prilaz se ne može primeniti u analizi kretanja deformabilnih tela. ), što, praktično, predstavlja nerešiv problem. Treći, čak i da možemo integraliti ovoliko veliki broj dinamičkih jednačina, određivanje integracionih konstanti, zbog principijelne nemogućnosti da istovremeno i tačno znamo položaj i brzinu svakog atoma u nekom početnom trenutku (početni uslovi), je nemoguće izvršiti. Međutim, čak i kada bismo mogli da nađemo konačne jednačine kretanja svih molekula, od ovakve detaljne slike ne bismo imali praktično nikakve koristi, jer bi prelaz na makroskopsku sliku zahtevao isuviše mnogo vremena. Prema tome, ovakav klasično-mehanički prilaz se ne može primeniti u analizi kretanja deformabilnih tela.Međutim, nezavisno od prethodnog zaključka, nas po pravilu ne interesuje praćenje kretanja pojedinačno svakog atoma, već nas interesuje kako se menjaju makroskopske karakteristike deformabilnih tela. Za makroskopsko proučavanje ovakvih sistema, koji sadrže veoma veliki broj čestica, koriste se dva opšta prilaza. Jedan od ovih opštih prilaza bazira na zakonima statističke fizike. U statističkom prilazu se polazi od realno postojeće situacije, odnosno od molekularne strukture sistema i sila koje vladaju među njima. Cilj je da se makroskopske karakteristike sistema objasne polazeći od osobina njegovih konstituenata (molekula) i njihove međusobne interakcije. Po pravilu, to obično nije moguće, već se osobine konstituenata kao i njihova međusobna interakcija aproksimiraju na pogodan način, da bi se mogla efektivno sprovesti teorijska analiza, odnosno da bi se odgovarajuće dinamičke jednačine mogle rešiti. Drugi opšti prilaz u analizi kretanja sistema sa velikim brojem čestica je fenomenološki, ili makroskopski metod. On bazira na fenomenološkoj teoriji u kojoj se razmatraju zakoni koji povezuju makroskopske (makrofizičke) karakteristike sistema. Do ovih zakonitosti se dolazi ili empirijski, ili na osnovu opštih principa (na primer, zakona održanja energije i njemu sličnih), koji su u krajnjem posledica iskustva. Fenomenološka teorija predstavlja efektivan metod za rešavanje mnogih važnih praktičnih problema. U ovom kursu mi ćemo koristiti fenomenološki prilaz u proučavanju kretanja deformabilnih sredina. U osnovi fenomenološke analize kretanja deformabilnih sredina leži aproksimacija po kojoj se stvarni diskretni raspored masa u njima zamenjuje kontinuumom, odnosno uzima se da su makroskopske karakteristike ovih sredina neprekidne funkcije prostornih koordinata i vremena. Ilustrujmo ovo na primeru vazduha. Pri normalnim uslovima (temperatura 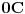 i atmosferskom pritisku na nivou mora) u jednom i atmosferskom pritisku na nivou mora) u jednom 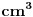 vazduha ima vazduha ima 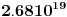 molekula. Ako u ovoj zapremini uzmemo kocku čija je stranica molekula. Ako u ovoj zapremini uzmemo kocku čija je stranica 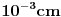 , što je često unutar tačnosti merenja dužine u praksi, u njoj će se nalaziti , što je često unutar tačnosti merenja dužine u praksi, u njoj će se nalaziti 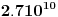 molekula vazduha. Prema tome, ogromno mnogo molekula se nalazi čak i u veoma malim zapreminama, zbog čega se približno, a istovremeno i zadovoljavajuće tačno, može smatrati da je masa tela raspoređena kontinualno, odnosno na neprekidan način. Zahvaljujući ovoj idealizaciji (aproksimacija kontinuuma) pri proučavanju kretanja deformabilnih tela možemo koristiti matematičku analizu neprekidnih funkcija, diferencijalni i integralni račun, što u mnogome olakšava analizu ovih kretanja. U ovom smislu, mi ćemo u buduće deformabilna tela zvati neprekidnim sredinama. molekula vazduha. Prema tome, ogromno mnogo molekula se nalazi čak i u veoma malim zapreminama, zbog čega se približno, a istovremeno i zadovoljavajuće tačno, može smatrati da je masa tela raspoređena kontinualno, odnosno na neprekidan način. Zahvaljujući ovoj idealizaciji (aproksimacija kontinuuma) pri proučavanju kretanja deformabilnih tela možemo koristiti matematičku analizu neprekidnih funkcija, diferencijalni i integralni račun, što u mnogome olakšava analizu ovih kretanja. U ovom smislu, mi ćemo u buduće deformabilna tela zvati neprekidnim sredinama.[ petarm @ 26.04.2008. 20:30 ] @
Priroda je vec sama dovoljno komplikovana i ti Mikky ne mozes da stignes na more ni avionom, a kamoli puzeci!
[ zzzz @ 27.04.2008. 00:58 ] @
Nedeljko je u prvoj poruci izneo tezu:
..ne postoji nikakva esencijalna potreba za mernim jeinicama, već eventualno praktična.. A kasnije još i ovo: E, sad ide ono glavno. Merne jedinice imaju svoje definicije, to jest, ne spadaju u osnovne, već u izvedene pojmove. … …. Dakle, pošto spadaju u izvedene pojmove, uvek se mogu eliminisati, to jest, sve što može sa njima, može i bez njih. Ja mislim da nije tako.A evo zašto: Da bi algebarski opisali neki fizički zakon moramo:a) Fizikalne pojmove izraziti brojevima. b)Napraviti idealizirani model te pojave. (Inače ne ide) **Da bi fizičke pojmove izrazili brojevima moramo uvesti jedinicu mjere. (Inače ne ide) Mjerni broj nije neimenovan već imenovan.Imenovanjem (jedinicom mjere) ujedno navodimo i karakter fizikalnog pojma. Pokazalo se da se ovako opisani zakoni mogu kombinovati i razrađivati dalje po jasnim pravilima matematike.Eksperimentalna fizika je potvrđivala matematička predviđanja. ----------------------------- ** jedinice mjere su standardizovane iz praktičnih razloga. **JM je definisana pomoću etalona. ** JM i etalon mjere su različiti pojmovi.Naprimjer za metar je etalon-« najbolji atomski sat i brzina svjetlosti», a za masu nekakav uteg u Parizu. SI sistem nije racionaliziran matematički nego tehnološki.Zato imamo neke osnovne jedinice mjere koje bi se mogle izraziti i pomoću drugih osnovnih jedinica.Naprimjer stepen kelvina bi mogli izraziti metrom i sekundom,ali kako bi baždario termometar? Mjeriti prosječne brzine atoma nekakvim mikrskopom?Ne.Bolje je ovako kako je usvojeno. [ Nedeljko @ 27.04.2008. 09:54 ] @
Neki očigledno nisu pažljivo čitali moje poruke.
Ako ja kažem da je dijagonala mog monitora 17, to zaista ne znači ništa, ali ako kažem da je n puta kraće od rastojanja Mesec-Zemlja, gde je n tačno određeni broj, onda sam ja izrazio veličinu mog monitora. Da bi izrazio odnos dve veličine isog karaktera (obe dužine ili obe snage itd.) ne treba mi nikakva merna jedinica, a to je jedino što zaista mogu da izrazim. Kada kažem da je dijagonala mog monitora 17 inča, izrazio sam odnos dijagonale mog monitora i rtalona inča, baš kao što sam dijagonalu monitora mogao da izrazim i preko odnosa sa rastojanjem od Zemlje do Meseca. Međutim, izražavanje u inčima je praktičnije jer se na svakom ćošku može kupiti instrument za merenje dužine u inčima (ili u metrima, pa da se izvrši konverzija). Sa druge strane, ako se definicija ne može eliminisati iz svih iskaza i svih dokaza, onda ta definicija nije korektna. Drugim rečima, ako je merne jedinice nemoguće eliminisati, onda ih je nemoguće i definisati. [ zzzz @ 27.04.2008. 10:39 ] @
Nedeljko.Da bi izrazio odnos dve veličine isog karaktera (obe dužine ili obe snage itd.) ne treba mi nikakva merna jedinica, ....
Pa tu već imaš mjernu jedinicu.Jednu veličinu izražavaš pomoću omjera sa drugom. Ova druga ti je mjerna jedinica i mora biti definirana. Sa druge strane, ako se definicija ne može eliminisati iz svih iskaza i svih dokaza, onda ta definicija nije korektna. Drugim rečima, ako je merne jedinice nemoguće eliminisati, onda ih je nemoguće i definisati. Dakle nešto kao svođenje na aksiome u matematici. SI sistem sa 6 osnovnih mjernih jedinica bi se mogao mat.racionalizacijom svesti na samo dvije.A ove dvije (za vrijeme i masu) bi se definirale sa nekoliko postulata (aksioma fizike).Postulati su iskustveno uočeni i smatraju se vremenski nepromjenjivim pojmovima. Zamjena standardne mjerne jedinice postulatima na kojima počiva je moguća.Tako se obično radi u labaratorijama pri izvođenju eksperimenata. [ petarm @ 27.04.2008. 11:51 ] @
A kolko je rastojanje izmedju Zemlje i Meseca?
[ Nedeljko @ 27.04.2008. 13:21 ] @
@petarm
Ja tvrdim da se rastojanje izmedju Zemlje i Meseca ne može izraziti bez poređenja sa nekom drugom dužinom, tako da bi na to pitanje ti trebao da daš odgovor. Jeli Petre, koliko je rastojanje između Zemlje i Meseca? @zzzz Citat: zzzz: Pa tu već imaš mjernu jedinicu.Jednu veličinu izražavaš pomoću omjera sa drugom. Ova druga ti je mjerna jedinica i mora biti definirana. Znači, svaka moguća dužina je merna jedinica za dužinu, budući da mogu govoriti o odnosu bilo koje dve dužine. Rastojanje između bilo čega bilo čega je merna jedinica za dužinu. Zanimljivo. Po tome ispada da je merna jedinica = veličina. OK, zašto se onda uvodi još jedan termin (merna jedinica) za isti pojam (veličine)? Još će da ispadne da su merne jedinice izmišljene da bi nam zakomplikovale život, a ne da bi nam ga olakšale. Citat: zzzz: Dakle nešto kao svođenje na aksiome u matematici. SI sistem sa 6 osnovnih mjernih jedinica bi se mogao mat.racionalizacijom svesti na samo dvije. SI sistem ima 7 osnovnih jedinica (Kg,m,s,mol,K,A,cd), a ostale su izvedene (m/s, cm, s2,...). No, ja ne govorim o osnovnim i izvedenim jedincama, već o osnovnim i izvedenim pojmovima. Jedinicu kao pojam možeš svoditi na druge jedinice, a možeš i opštije, da je kao pojam svodiš na druge pojmove (koji ne moraju biti jedinice). Osnovni pojam je pojam koji se ne definiše, a izvedeni je onaj koji ima definiciju. U SI sistemu postoje definicje sedam osnovnih mernih jedinica. [ Časlav Ilić @ 27.04.2008. 19:54 ] @
Citat: Nedeljko: [...] ne postoji nikakva esencijalna potreba za mernim jeinicama, već eventualno praktična [...] Citat: Po tome ispada da je merna jedinica = veličina. OK, zašto se onda uvodi još jedan termin (merna jedinica) za isti pojam (veličine)? Još će da ispadne da su merne jedinice izmišljene da bi nam zakomplikovale život, a ne da bi nam ga olakšale. Ja bih rekao, merna jedinica = etalon veličine (fizičke dimenzije). Način izražavanja količine neke dimenzije, pa tako zaista čisto praktične upotrebne vrednosti. Onda različite jedinice imamo prosto jer je mozgu lakše da upoređuje brojeve s malo značajnih cifara, recimo do tri. Gde je neophodno brzo delovanje obično se jedinice podrazumevaju; npr. kad nešto ručno merimo u laboratoriji, obično izvikujemo samo brojeve, jer se jedinica podrazumeva: „Protok 17, pritisak 158!“ misleći na litre u sekundi i kilopaskale. Tako da su merne jedinice tu zaista da bi nam olakšale život, gde mi = inženjeri. S druge strane, prema ličnom iskustvu, matematičarima je najbolje ispostavljati jednačine u bezdimenzionom obliku :) Matematičar koji radi u korist inženjerskog problema uopšte ne mora da se bakće s jedinicama. Tako su vuci siti i koze na broju. Ali, rekao bih da je navođenjem jedinice mnogo bitnije to što se posredno ukazuje na fizičku dimenziju, ono na šta su Makraken i Fitopatolog zapravo ukazivali pominjanjem baba i žaba i provere formula. Posebno pritom mislim na Bakingemovu π-teoremu; npr. svaki pravi vazduhoplovac zna da avion leti zbog Bakingemove π, a da je sve ostalo nagvaždanje fizičarâ :) [ zzzz @ 27.04.2008. 21:23 ] @
Nedeljko : U SI sistemu postoje definicje sedam osnovnih mernih jedinica.
Ima gotovo 30 godina kako metar nije osnovna jedinica SI.A i onaj etalon-šipka je otišao u muzej.Usvojena je brzina svjetlosti c=299 792 458 m/s i zaleđena.Nema više još preciznijeg mjerenja c. Gotovo je s tim.Metar je izvedena vrijednost iz ovog broja i etalona sekunde. Potrudi se da shvatiš o čemu je riječ. (Prikačio sam nešto uz prošlu poruku.) Ja tvrdim da se rastojanje izmedju Zemlje i Meseca ne može izraziti bez poređenja sa nekom drugom dužinom ??? Osim ako se ne poredi sama sa saobom.Tada bi to rastojanje bilo mjerna jedinica (zm), a udaljenost Zemlja Mjesec: l= 1 (zm). Znači, svaka moguća dužina je merna jedinica za dužinu, budući da mogu govoriti o odnosu bilo koje dve dužine. Rastojanje između bilo čega ** merna jedinica za dužinu. Zanimljivo. Po tome ispada da je merna jedinica = veličina. a)Da ako je neko usvoji i definiše. b)Isto kao pod a) c)Da!I dali smo joj modul 1! ---------------------- Astronomi vole da udaljenost Sunce-Zemlja uzmu za jedinicu (L(s-z)=1), pa onda okolo mjere sa tom dužinom.A neki opet vole da im je put svjetlosti za godinu dana jednak 1.Šta možemo kad ima svakakvih ljudi. ČaslavJa bih rekao, merna jedinica = etalon veličine (fizičke dimenzije) Ponekad da, ali ne uvijek.Obično etalon služi za baždarenje mjernih instrumenata tj. mjerne jedinice.To je zakonom propisano.Imamo etalon etalona, pa i unuče etalona sa potrebnim pedigreom i papirima.(Državni zavodi za mjere utege i dragocjenosti.) [ Nedeljko @ 28.04.2008. 08:08 ] @
Citat: zzzz: Ima gotovo 30 godina kako metar nije osnovna jedinica SI.A i onaj etalon-šipka je otišao u muzej.Usvojena je brzina svjetlosti c=299 792 458 m/s i zaleđena.Nema više još preciznijeg mjerenja c. Znam da je metar definsan preko brzine svetlosti i sekunde. No, on se i dalje smatra osnovnom jedincom SI sistema. http://en.wikipedia.org/wiki/International_System_of_Units#Units Ljudi su se jednostavno dogovorili da u izrazu m/s ne vrše skraćvanje, to jest, da brzina nije bezdimenziona veličina, a moglo bi i tako. Na isti način kao što možeš metar da definišeš preko brzine svetlosti i sekunde, mogao bi da definišeš i kilogram preko, metra, sekunde i gravitacione konstante, a pošto je metar prethodno sveden na sekundu, da svedeš i kilogram na sekundu. Slično, kelvin možeš predstaviti kao m2/s2 puta neki broj (bezdimenziona veličina), jer je temperatura idealnog gasa ništa drugo do mera ukupne kinetičke energije čestica od kojih se gas sastoji po masi tog gasa. Amper možeš definisati kao džul podeljen sa naelektrisanjem jednog elektrona i ponmožen sa nekom bezdimenzionom jedinicom. No, ljudi su se dogovorili da između tih mernih jedinica ne vrše skraćivanje. Sa druge strane, dogovorili su se da za tromu i tešku masu koriste istu jedinicu, dok neko ne utvrdi postojanje razlike. Citat: zzzz: a)Da ako je neko usvoji i definiše. Upravo je to suštinski uslov da nešto bude merna jedinica. Ali, ja mogu da poredim bilo koje dve dužine, čak i ako nijedna od njih nije dogovorena jedinica (bez dogovora nema ni jedince). [ petarm @ 28.04.2008. 11:20 ] @
@Nedeljko
Znači, svaka moguća dužina je merna jedinica za dužinu, budući da mogu govoriti o odnosu bilo koje dve dužine. Rastojanje između bilo čega bilo čega je merna jedinica za dužinu. Zanimljivo. Po tome ispada da je merna jedinica = veličina. OK, zašto se onda uvodi još jedan termin (merna jedinica) za isti pojam (veličine)? Još će da ispadne da su merne jedinice izmišljene da bi nam zakomplikovale život, a ne da bi nam ga olakšale. Nije tako. Ali svaku duzinu mozes uzeti kao mernu jedinicu za duzinu. U zavisnosti od potrebe. Zato se u astronomiji uzima npr. parsek. [ Nedeljko @ 28.04.2008. 14:39 ] @
Ama, taj citat se odnosi na zzzz-ovu izjavu i ne može se izvaditi iz tog konteksta. Naravno da svaku dužinu možemo izabrati za mernu jedinicu, ali isto tako možemo i bez ikakve merne jedinice za dužinu, već da govorimo isključivo o odnosima dužina, koji ne zavise od izbora mernih jedinica.
[ Sprečo @ 04.05.2008. 21:37 ] @
Da je „problem“ upoređivanja veličina (jedinice, transformacija mjernih brojeva,...) bio obrazložen i povezan sa STR (posebno vezano za frekvencije, talasne dužine i „unutrašnje“, „sopstveno“ vrijeme vezano za brzinu svjetlosti i talasne dužine, te miješanje „baba i žaba“ u Lorencovim formulama, „kvadrivektorima“- matricama) vjerovatno bi diskusija u ovoj temi bila bogatija i sadržajnija.
U pokušaju da podstaknem diskusiju probao sam (ovdje) ubaciti formule, ali mi to (ponovo) ne ide. [ cicika @ 12.06.2008. 23:36 ] @
Citat: Zašto rezultat "dužina moje sobe je četiri puta veća od visine mog prozora" bez jedinica ne znači ništa? Ali ti si ovde iskoristio jedinicu... ili ako hoćeš etalon, ali tvoja jedinica nije standardna. Njen naziv glasi "visina mog prozora". Korišćenje jedinica nije ništa drugo nego poredjenje sa etalonom odredjenog naziva. Dakle... 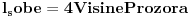 [ zzzz @ 13.06.2008. 01:04 ] @
Ovo što cicika kaže je OK.To je već ranije spomenuto.Ali da se podsjetimo na start:
Nedeljko je rekao: "Raspravljao sam se sa kolegama na poslu i nikako da ih ubedim da ne postoji nikakva esencijalna potreba za mernim jeinicama, već eventualno praktična, pa me zanima kako drugi razmišljaju o tome. Kada kažem da je dijagonala mog monitora iznosi 0.432 m, ja sam zapravo izrazio odnos dveju dužina: dijagonale mog monitora i etalona metra. Taj iskaz se u suštini ne razlikuje od iskaza: dijagonala mog monitora je 3 puta kraća od visine mog prozora. Jedino što zaista mogu izraziti je odnos između dve dužine, bez obzira da li je imenilac neki dogovoreni etalon ili neka druga dužina, a da bih izrazio odnos između dveju dužina, ne treba mi nikakav sistem mernih jedinica. Rezultat je čist realan broj bez dimenzije, koji ne zavisi od izbora mernih jedinica." A nešto kasnije spominje i mjerenje uglova (radijan).Izgleda da je on baš tu zalutao, jer za mjerenje ugla stvarno je nepotrebno uvoditi jedinicu za mjerenje dužine. Lijep logički zaključak: 1)Ugao je omjer dužine luka i dužine radijusa koji ga opisuje.(Pa onda slijedi:) 2)Bez obzira koji etalon mjere koristili, ovaj omjer će biti uvijek isti..(Pa onda slijedi:) 3)Etalon mjere nam ne treba, a ako ga neko već koristi to je samo iz praktičnih razloga. .(Pa onda slijedi:) 4)Omjer između dvije dužine se može uzraziti brojem, a da se te dužine prethodno i ne mjere standardnim etalonom dužine..(Pa onda slijedi:) 5)Ima li potrebe za mjernim jedinicama? NE, misli Nedeljko. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|