Pogledao sam u Grulinim grupama.
Teorema 20.1
Grupa je Hamiltonova akko je direktni proizvod jedne grupe kvaterniona sa Abelovom grupom ciji su elementi neparnog reda i Abelovom grupom ciji su elementi reda najvise 2.
(Dokaz je uzasan)
Korolar 20.2
(a) Osim grupe kvaterniona svaka Hamiltonova grupa je razloziva.
(b) Direktni proizvod dve (ili vise) Hamiltonove grupe nije Hamiltonova grupa
(c) U Hamiltonovoj grupi su elementi uzajamno prostih redova permutabilni.
Odavde sam jedino zakljucio da grupa kvaterniona nije direktni proizvod netrivijalnih normalnih podgrupa

Verovatno se negde ranije spominju grupe kvaterniona u knjizi, al ne mogu da nadjem gde.
Naisao sam inace na ovaj izraz
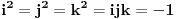
u jednom udzbeniku iz mehanike.
Da inace jel ovo nerazloziva sinonim sa ireducibilna?