1.) Knjiga Boze Milica je jako ispretumbana i prepunjena cinjenicama, ali rekao bih kao da nije do kraja dorecena. Npr. str. 194. kaze:
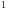
Koliki je to relativno mali broj stepeni slobode?
+ ne mogu da nadjem gde to Boza radi u svojoj knjizi.
3.) Hocu da kazem da su neki autori ''na prste'' zakljucili da izvod i varijacija komutiraju!
4.)
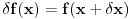
ali mi smo rekli kod uvodjenja te tzv. Lagranzeve varijacije da nezavisno promenljivu ne variramo. A ovde se pojavi
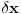
. Ne kazem da nisi u pravu! Samo mi je ovaj deo problematican.