[ markob15 @ 08.05.2008. 21:56 ] @
| Potrebni privatni casovi iz linearne algebre. Student matematickog fakulteta. Beograd. |
|
[ markob15 @ 08.05.2008. 21:56 ] @
[ nemanja168 @ 12.09.2008. 18:37 ] @
Pa i ja trazim nekog ko bi mi objasnio par stvari...ima li takvih...?
[ vriskica @ 12.09.2008. 19:11 ] @
sta nije jasni iz tog predmeta..polozila sam taj predemet..pa ako budem sta znala da objasnim..
[ Cabo @ 12.09.2008. 20:17 ] @
Samo pitaj. Linearna je po mom skromnom mišljenju najlakši matematički predmet na MATF-u. A inače već neko vreme razmišljam o držanju privatnih časova. Ovo će biti „uhodavanje“ za tako nešto.
[ peromalosutra @ 15.09.2008. 19:59 ] @
Evo ako dozvolite da ja uskočim sa jedim zadatkom. U pitanju su linearni operatori, nije mi baš najjasnije kakva je veza između linearnog operatora i baze u vektorskom prostoru, te načina na koji se to predstavlja matricom. Ako nije problem, bilo bi dobro kada bi neko uradio sledeći zadatak (ili naveo linkove ka konkretnoj literaturi koja pokriva ovaj dio, jer je ova oblast dosta slabo pokrivena u knjigama koje imam):
Neka je T: P1->P2 linearno preslikavanje dato sa T(a+bx)=a+b+(2a-3b)x. Neka je A matrica tog preslikavanja u bazi {1,x}, a B u bazi {1+x,1-x}. Naći matrice A i B, te izračunati A^n. Ovaj drugi dio zadatka (izračunati A^n) ne bi trebao biti problem i mislim da bih to mogao uraditi indukcijom ili preko binomne formule, ali problem je prvi dio zadatka, kako odrediti ove dve matrice? Hvala [ Cabo @ 17.09.2008. 18:44 ] @
Citat: peromalosutra: Neka je T: P1->P2 linearno preslikavanje dato sa T(a+bx)=a+b+(2a-3b)x. Neka je A matrica tog preslikavanja u bazi {1,x}, a B u bazi {1+x,1-x}. Naći matrice A i B, te izračunati A^n. Ovaj drugi dio zadatka (izračunati A^n) ne bi trebao biti problem i mislim da bih to mogao uraditi indukcijom ili preko binomne formule, ali problem je prvi dio zadatka, kako odrediti ove dve matrice? 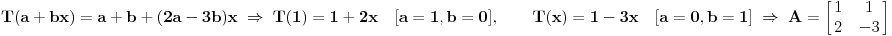 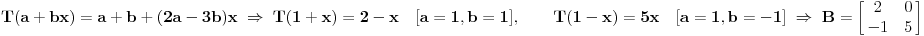 Jel' u redu? Poenta je da napraviš matricu koja se sastoji od vrednosti operatora nad vektorima baze: 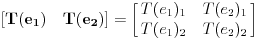 [Ovu poruku je menjao Cabo dana 17.09.2008. u 20:17 GMT+1] [ peromalosutra @ 18.09.2008. 16:49 ] @
Ovaj primjer sam shvatio, možeš li mi još samo pojasniti tu istu stvar na primjeru prostora matrica?
Recimo da je zadan prostor M koji se sastoji iz 2x2 matrica i neka je zadan linearni operator L(A)=A^t (A transponovano). Standardne baze su (očigledno): Code: |1 0| |0 1| |0 0| |0 0| e1=|0 0|, e2=|0 0|, e3=|1 0|, e4=|0 1| Ako ove baze uvrstim u operator L(A) dobijam: Code: |1 0| |0 0| |0 1| |0 0| L(e1)=|0 0|, L(e2)=|1 0|, L(e3)=|0 0|, L(e4)=|0 1| Kako u ovom slučaju izgleda matrica linearnog operatora? Trebala bi da ima 2 vrste da bi uopšte mogla da se pomnoži sa nekom matricom iz M? [ Cabo @ 19.09.2008. 12:25 ] @
Hm, e ovde bi moji asistenti pitali: „A odakle ti ovaj primer?“
Ne, ozbiljno, ovo je vrlo zanimljiv primer, i mogu samo da nagađam da se tu, ako formalno primenimo teoriju, pravi matrica čiji su elementi matrice. Sad neću da lupam, ali sam načuo nešto da bi to mogli da budu tenzori ili slično, ali to svakako ne spada u gradivo Linearne algebre. Poenta je da dobiješ 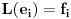 , , 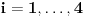 , gde su , gde su 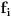 matrice umesto skalara. To kako se množi ova „matrica matrica“ zavisi od definicije operacije nad njima, pa tako možemo imati neko matrice umesto skalara. To kako se množi ova „matrica matrica“ zavisi od definicije operacije nad njima, pa tako možemo imati neko  koje definišemo kao proizvod matrica, i onda množimo elemente takvih „matrica“ preko te operacije. Ali sve ovo sam ja sada iskonstruisao na osnovu onoga sa čim sam se sretao iz Linearne i ne mogu sa sigurnošću da kažem da li je to pravi način da se reši ovaj zadatak. koje definišemo kao proizvod matrica, i onda množimo elemente takvih „matrica“ preko te operacije. Ali sve ovo sam ja sada iskonstruisao na osnovu onoga sa čim sam se sretao iz Linearne i ne mogu sa sigurnošću da kažem da li je to pravi način da se reši ovaj zadatak.[ Nedeljko @ 19.09.2008. 12:45 ] @
Matrica linearnog operatora prostora dimenzije 4 ima format 4x4.
[ icobh @ 19.09.2008. 15:35 ] @
@peromalosutra
Očigledno je da studraš ETF i da si bio nekidan (9.9.2008) na ispitu?! :D I ja sam i jedino što sam znao je treći zadatak ali nisam htjeo predati prijavu već sam ju zgužvao i bacio u smeće... [ peromalosutra @ 19.09.2008. 17:15 ] @
Citat: ali nisam htjeo predati prijavu već sam ju zgužvao i bacio u smeće... To je bilo u sred ispita? Ako jeste onda se sjećam te scene. :) I ja sam uradio 3. mada nisam ništa učio linearne operatore, tako da to dovoljno govori o njegovoj težini (to i činjenica da je nosio samo 10 bodova). Mislim da u utorak rok daje prof. Ćelić, asistenti su valjda otišli, tako da će tek to biti zabavno. :) Pozz [ icobh @ 19.09.2008. 17:32 ] @
Da u sred ispita. Prvo sam bio izašao pa se vratio i pitao da li mogu da uzmem svoju prijavu, da je lično bacim u smeće. Tako je i bilo na kraju.
A sad, vidiš kako čovjek uradi ovaj 5-ti zadatak!? Ni na kraj pameti mi nije bilo da uradim ovo, jer ovo pomalo prevazilazi samu Algebru u ulazi u neke tokove caka. Malte ne, mi moramo sem teorije i zadataka, znati šta su asistenti imali na umu kad su pisali zadatak. Mnogo moramo izvlačiti od njih, a slabo šta govore... [ Cabo @ 20.09.2008. 18:29 ] @
Citat: Nedeljko: Matrica linearnog operatora prostora dimenzije 4 ima format 4x4. Da, slažem se, samo što su ovde „vektori“ matrice. Prostor 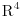 jeste izomorfan prostoru jeste izomorfan prostoru 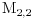 , ali nije i identičan! , ali nije i identičan!Mislim, možeš ti da kažeš 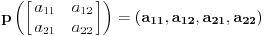 , pa onda da kažeš recimo , pa onda da kažeš recimo 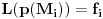 i da formiraš matricu, ali to nije po teoriji... i da formiraš matricu, ali to nije po teoriji...Da budem jasniji, ovde se priča o sledećem: 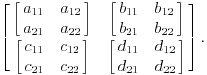 [Ovu poruku je menjao Cabo dana 20.09.2008. u 20:50 GMT+1] [ Cabo @ 22.09.2008. 13:01 ] @
Šta? Nema komentara? Jesam li u pravu? U suprotnom, gde grešim?
[ icobh @ 22.09.2008. 15:19 ] @
Evo imam ja komentar ali na ovaj predhodni zadatak. Pošto ne znam sve detalje, reći ću samo ono što je meni jedan kolega rekao, on je valjda išao kod asistenta. Valjda matrica A je OK ali B nije. To je sve što sam saznao i ne mogu ništa više da kažem, jer ova matematika meni stvarno ne ide. Analiza, Vjerovatnoća, Statistika, Diskretna idu nekako ali Algebra...
[ Cabo @ 22.09.2008. 18:51 ] @
[ peromalosutra @ 22.09.2008. 19:01 ] @
[ Cabo @ 22.09.2008. 20:42 ] @
Citat: peromalosutra: Obe matrice u prvom zadatku su tačne. A što se tiče drugog zadatka, upravo su i mene zbunjivale dimenzije matrice operatora. Prema ovome što je Cabo napisao, matrica linearnog operatora bi onda trebala da izgleda: 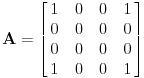 Da li sam u pravu? Ili tako, ili (ako kreneš preko preslikavanja koje sam ja označio sa 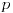 , na šta je izgleda ciljao Nedeljko, ali je malo škrt na rečima pa neće da potvrdi to svoje mišljenje :-/ ): , na šta je izgleda ciljao Nedeljko, ali je malo škrt na rečima pa neće da potvrdi to svoje mišljenje :-/ ):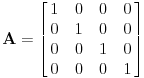 [ Cabo @ 23.09.2008. 11:07 ] @
[smajli koji se lupa šakom po čelu i udara glavom u zid]
Ovo me je zaintrigiralo do te mere da sam uzeo svoju staru zbirku iz Linearne, „Linearna algebra: Zbirka rešenih zadataka“ od Stojana i Davora Radenovića, Beograd, 1996., i podsetio se zadataka koje sam radio toliko davno da sam potpuno zaboravio na njih. Izgleda da ću morati da malo i obnavljam Linearnu ukoliko želim da držim časove iz nje.  Sad mi je jasno i zašto se dobijaju vektori. U suštini, ti uvek treba da dobiješ vektor, jer se gledaju koordinate u odnosu na bazu, što znači: 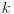 -torka skalara, gde je -torka skalara, gde je 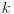 dimenzija prostora nad kojim je definisan operator dimenzija prostora nad kojim je definisan operator 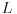 . .[Ovu poruku je menjao Cabo dana 23.09.2008. u 12:22 GMT+1] [ icobh @ 24.09.2008. 16:06 ] @
Citat: Cabo: Tako je! Treba uraditi još i: 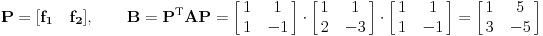 Bilo bi veoma lepo ako bi neko otišao kod tog asistenta i pitao ga da li je ova matrica 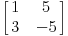 ispravna. ispravna.[Ovu poruku je menjao Cabo dana 22.09.2008. u 21:30 GMT+1] Ispravna matrica je: 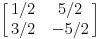 [ Nedeljko @ 25.09.2008. 11:10 ] @
Citat: peromalosutra: Ovaj primjer sam shvatio, možeš li mi još samo pojasniti tu istu stvar na primjeru prostora matrica? Recimo da je zadan prostor M koji se sastoji iz 2x2 matrica i neka je zadan linearni operator L(A)=A^t (A transponovano). Standardne baze su (očigledno): Code: |1 0| |0 1| |0 0| |0 0| e1=|0 0|, e2=|0 0|, e3=|1 0|, e4=|0 1| Ako ove baze uvrstim u operator L(A) dobijam: Code: |1 0| |0 0| |0 1| |0 0| L(e1)=|0 0|, L(e2)=|1 0|, L(e3)=|0 0|, L(e4)=|0 1| Kako u ovom slučaju izgleda matrica linearnog operatora? Trebala bi da ima 2 vrste da bi uopšte mogla da se pomnoži sa nekom matricom iz M? Matrica linearnog operatora se definise u odnosu na neku bazu. Ako je 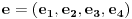 baza vektorskog prostora baza vektorskog prostora  , onda je matrica linearnog operatora , onda je matrica linearnog operatora 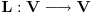 u odnosu na bazu u odnosu na bazu  zapravo matrica zapravo matrica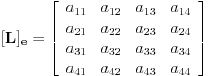 nad poljem skalara vektorskog prostora  takva da je takva da je 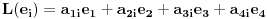 za za 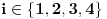 . To je definicija. U nasem slucaju je . To je definicija. U nasem slucaju je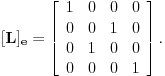 [ Cabo @ 25.09.2008. 22:23 ] @
[ icobh @ 25.09.2008. 22:28 ] @
Kada se uvrste baze 1-x i 1+x gore u zadatku i dobije se matrica B, ona je i dalje u standardnoj bazi jer priznaćeš da se 1-x i 1+x može dobiti linearnom kombinacijom članova baze P1 {1,x}, a nama treba matrica koja je u bazi {1-x ,1+x}...
100% tačno. Ja kad sam prihvatio ovo za rješenje, nije bilo problema, čak sam i ja sad položio Algebru... [ Cabo @ 25.09.2008. 22:36 ] @
Citat: icobh: Kada se uvrste baze 1-x i 1+x gore u zadatku i dobije se matrica B, ona je i dalje u standardnoj bazi jer priznaćeš da se 1-x i 1+x može dobiti linearnom kombinacijom članova baze P1 {1,x}, a nama treba matrica koja je u bazi {1-x ,1+x}... ... i zato se formira proizvod 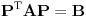 , da bi se prešlo na novu bazu. Da, ali to ne objašnjava zašto je ta „ispravna“ matrica dva puta manja od moje matrice. , da bi se prešlo na novu bazu. Da, ali to ne objašnjava zašto je ta „ispravna“ matrica dva puta manja od moje matrice.[ Nedeljko @ 26.09.2008. 08:24 ] @
Ljudi, ne rade se zadaci pre teorije. Prvo morate znati definicije i stavove da biste mogli da radite zadatke. Znam ja da mnogi studenti rade prvo zadatke, ali to je vrlo pogrešno i onda dolazi do ovakvih stvari.
[ peromalosutra @ 26.09.2008. 10:41 ] @
Citat: Nedeljko: Ljudi, ne rade se zadaci pre teorije. Prvo morate znati definicije i stavove da biste mogli da radite zadatke. Znam ja da mnogi studenti rade prvo zadatke, ali to je vrlo pogrešno i onda dolazi do ovakvih stvari. Naravno, po meni bi se prvo trebala i polagati teorija, znači teoreme neki principi,metode i njihovi dokazi, pa kad se to prođe onda tek ide "praktična" primjena u zadacima. Kod nas na ispitu od 5 zadataka bar 3 budu sa linearnim operatorima (dobro i ne budu toliko teški), a linearni operatori uopšte nisu pokriveni u zbirkama koje su nam preporučili. Ok, studenti smo pa ćemo se snaći, zato sam i postovao na ovoj temi. Citat: icobhJa kad sam prihvatio ovo za rješenje, nije bilo problema, čak sam i ja sad položio Algebru... Čestitam, btw i ja sam položio. [ Cabo @ 26.09.2008. 16:21 ] @
Citat: Nedeljko: Ljudi, ne rade se zadaci pre teorije. Prvo morate znati definicije i stavove da biste mogli da radite zadatke. Znam ja da mnogi studenti rade prvo zadatke, ali to je vrlo pogrešno i onda dolazi do ovakvih stvari. Ja sam položio Linearnu (pismeni i usmeni) 2000. godine. Ali hajde ti, koji „znaš“ teoriju, objasni mi zašto ja dobijem (preko programa Matematika) matricu koja je dva puta veća od one za koju je jedan od učesnika rekao da je ispravna? [ icobh @ 26.09.2008. 21:05 ] @
(2-X) = a(1+X) + b(1-X)
(2-X) = (a+b) + aX - bX (2-X) = (a+b) + (a-b)X a+b=2 a-b=-1 a=1/2, b=3/2 i još jednom za 5X [ Nedeljko @ 27.09.2008. 11:44 ] @
Citat: Cabo: Ja sam položio Linearnu (pismeni i usmeni) 2000. godine. Ali hajde ti, koji „znaš“ teoriju, objasni mi zašto ja dobijem (preko programa Matematika) matricu koja je dva puta veća od one za koju je jedan od učesnika rekao da je ispravna? 1. Nigde u teoriji ne piše šta ispaljuju kompjuterski programi. 2. Ne odgovaram ni za softver koji nisam pisao, ni za izjave drugih učesnika. Tačan rezultat je 4x4 matrica, jer je prostor četvorodimenzioni, koja zavisi od izbora baze i to sam odmah rekao. Citat: Nedeljko: Matrica linearnog operatora prostora dimenzije 4 ima format 4x4. Da si obnovio definiciju linearnog operatora, ne bi lutao, već bi odmah rešio zadatak. Šta ispaljuje Mathematica? Nije valjda 8x8 matrica? [ petarm @ 27.09.2008. 13:36 ] @
Citat: Ne razumem sta si hteo ovim da kazes u datom problemu? Kada radis tenzorski proizvod dve matrice 2x2 dobijes matricu 4x4, a kada radis tenzorski proizvod dve matrice 4x4 dobijes matricu 8x8. Ovde neceg slicnog nije bilo. Mozda te je to zbunilo? Citat: Nedeljko: Da si obnovio definiciju linearnog operatora, ne bi lutao, već bi odmah rešio zadatak. Šta ispaljuje Mathematica? Nije valjda 8x8 matrica? Nedeljko kolko sam ja shvatio matrica jeste 4x4, ali je duplo manja u smislu pomnozena sa 1/2. Pozdrav [ Nedeljko @ 27.09.2008. 16:24 ] @
[ Cabo @ 27.09.2008. 18:37 ] @
U redu, evo nacrtaću:
Kad ukucam: Code: P={{1, 1}, {1, -1}}; A={{1, 1}, {2, -3}}; Transpose[P].A.P dobijem Code: {{1, 5}, {3, -5}} Označimo matricu koju daje program Matematika sa 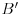 . Rečeno je da je ispravna matrica . Rečeno je da je ispravna matrica 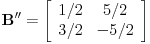 . Očito je . Očito je 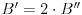 , odnosno matrica koju daje program Matematika je dva puta veća od matrice koja je označena kao „ispravna“. , odnosno matrica koju daje program Matematika je dva puta veća od matrice koja je označena kao „ispravna“.[Ovu poruku je menjao Cabo dana 27.09.2008. u 21:33 GMT+1] [Ovu poruku je menjao Cabo dana 27.09.2008. u 21:43 GMT+1] [ Nedeljko @ 28.09.2008. 10:06 ] @
[ petarm @ 28.09.2008. 10:50 ] @
Trebalo bi da je to ovaj zadatak
Neka je T: P1->P2 linearno preslikavanje dato sa T(a+bx)=a+b+(2a-3b)x. Neka je A matrica tog preslikavanja u bazi {1,x}, a B u bazi {1+x,1-x}. Naći matrice A i B, te izračunati A^n. [ Nedeljko @ 28.09.2008. 14:35 ] @
Samo me još zanima šta su P1 i P2.
[ Cabo @ 28.09.2008. 17:38 ] @
Citat: Nedeljko: Samo me još zanima šta su P1 i P2. Nadam se vektorski prostori. Dodatak: Sada mi je jasno zašto mi nije tačna matrica. Umesto 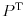 treba koristiti treba koristiti 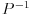 , jer se ne radi o ortonormiranim bazama, pa nije , jer se ne radi o ortonormiranim bazama, pa nije 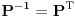 . :P . :P[Ovu poruku je menjao Cabo dana 28.09.2008. u 18:51 GMT+1] [ Nedeljko @ 28.09.2008. 18:09 ] @
Koji vektorski prostori?
[ Cabo @ 28.09.2008. 18:36 ] @
Citat: Nedeljko: Koji vektorski prostori? Koliko vidim (i ako se dobro sećam Algebre 1 koju sam položio nešto kasnije od Linearne, ali opet ne previše skoro), nešto tipa 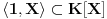 i i 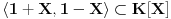 . .[ Nedeljko @ 28.09.2008. 20:03 ] @
Neka je
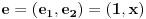 , , 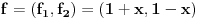 . Po definiciji je matrica . Po definiciji je matrica 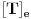 operatora operatora  u bazi u bazi  je matrica za koju važi je matrica za koju važi 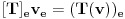 , gde je , gde je 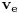 oznaka za vektor koordinata vektora oznaka za vektor koordinata vektora  u bazi u bazi  . Obzirom da je . Obzirom da je 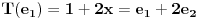 i i 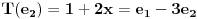 , važi , važi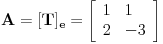 . .Vektori koordinata se upisuju po kolonama da bi bio zadovoljen uslov 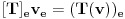 na baznim vektorima, a onda će na osnovu linearnosti važiti na celom vektorskom prostoru. Obzirom da je na baznim vektorima, a onda će na osnovu linearnosti važiti na celom vektorskom prostoru. Obzirom da je 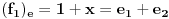 i i 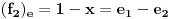 za matricu za matricu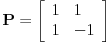 važi 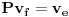 . Jednakost važi na vektorima baze . Jednakost važi na vektorima baze  , pa i na celom vektorskom prostoru. Množenjem poslednje jednačine sa , pa i na celom vektorskom prostoru. Množenjem poslednje jednačine sa 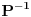 dobija se jednakost dobija se jednakost 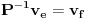 . Dakle, . Dakle, 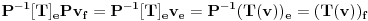 , pa je , pa je 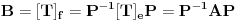 . Dakle, . Dakle,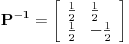 , ,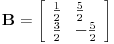 . .Treba li da računam  ? ?[ Cabo @ 28.09.2008. 20:36 ] @
Citat: Cabo: Dodatak: Sada mi je jasno zašto mi nije tačna matrica. Umesto 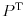 treba koristiti treba koristiti 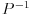 , jer se ne radi o ortonormiranim bazama, pa nije , jer se ne radi o ortonormiranim bazama, pa nije 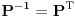 . :P . :PHvala na odgovoru, ali sam i sam utvrdio šta nije štimalo. Trenutno sam okrenut razmišljanju u kategorijama ortonormiranih baza, izometrija i sličnosti, pa sam pretpostavio da je 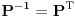 , što nije trebalo da uradim. To je bila greška. , što nije trebalo da uradim. To je bila greška.[ Nedeljko @ 29.09.2008. 08:12 ] @
U vektorskim prostorima nema smisla pojam ortonormirane baze. Taj pojam ima smisla samo u vektorskim prostorima snabdevenim skalarnim proizvodom. Koliko znam, onda je polje skalara R ili C, a ti si cak napisao da se ovaj problemn resava nad proizvoljnim poljem. Prethodno resenje vazi nad bilo kojim poljem karakteristike razlicite od 2, a nad poljima karakteristike 2 sistem (1+x,1-x) nije baza jer je linearno zavisan. Vazi 1+x=1-x u takvim poljnima, pa imamo sistem u kome se jedan vektor ponavlja dva puta.
[ Cabo @ 29.09.2008. 10:08 ] @
Citat: Nedeljko: U vektorskim prostorima nema smisla pojam ortonormirane baze. Taj pojam ima smisla samo u vektorskim prostorima snabdevenim skalarnim proizvodom. Koliko znam, onda je polje skalara R ili C, a ti si cak napisao da se ovaj problemn resava nad proizvoljnim poljem. Prethodno resenje vazi nad bilo kojim poljem karakteristike razlicite od 2, a nad poljima karakteristike 2 sistem (1+x,1-x) nije baza jer je linearno zavisan. Vazi 1+x=1-x u takvim poljnima, pa imamo sistem u kome se jedan vektor ponavlja dva puta. Odgovarao sam na brzinu, a sem toga: Citat: Cabo: Koliko vidim (i ako se dobro sećam Algebre 1 koju sam položio nešto kasnije od Linearne, ali opet ne previše skoro), nešto tipa 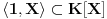 i i 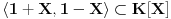 . .[ petarm @ 04.10.2008. 10:12 ] @
Kakav je udzbenik Linearna algebra i analiticka geometrija od Lipkovskog?
[ Cabo @ 04.10.2008. 18:15 ] @
Nemam pojma. Zar i on ima svoj udžbenik? Prvi put čujem za tako nešto.
[ Nedeljko @ 04.10.2008. 18:43 ] @
Sasvim OK.
[ petarm @ 04.10.2008. 18:53 ] @
Danas sam video knjigu pa razmisljam dal da je kupim?
[ Nedeljko @ 05.10.2008. 08:40 ] @
Konciznija je od nekih drugih knjiga iz linearne algebre, ali ne na račun gubljenja bitnih stvari.
[ Dusan Stojakovic @ 06.10.2008. 15:42 ] @
Pozdrav, jel' moze neko meni da preporuci koja je zbirka najbolja (zbirka resenih zadataka) iz Linearne Algebre???
Posto, prva sam godina i malo je kako vidim zapetljana Linearna Algebra na ETF u BL (a gde nije???)... Zato rekoh da pitam odakle je najbolje da krenem, da bih uspio poloziti ispit i kolokvije... [ Cabo @ 06.10.2008. 17:25 ] @
Pa evo, ja sam već naveo Radenovićevu zbirku, po njoj je radila moja generacija na MATF-u.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|