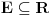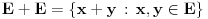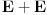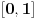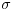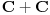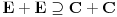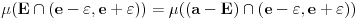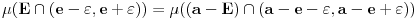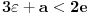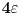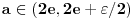[ Nedeljko @ 16.05.2008. 08:20 ] @
|
[ Nedeljko @ 23.05.2008. 11:32 ] @
Zar niko ne moze da resi ovaj zadatak? Ja ne umem da ga resim i zivo bi me zanimalo da vidim resenje.
[ Farenhajt @ 23.05.2008. 22:42 ] @
Što bi se ovde reklo: "Zar očekuješ da ti se domaći servira na tacni?"
[ Nedeljko @ 25.05.2008. 17:45 ] @
Prvo, imam previse godina da bih imao domaće zadatke.
Drugo, lepo sam napisao dokle sam stigao - do svođenja opšteg slučaja na slučaj kompaktnih skupova, a dalje ne umem. Treće, ne očekujem ni kompletno rešenje, nego bar neku ideju za početak. Četvrto, više godina sam posećivao ovaj forum i priložio mnoga rešenja. Voleo bih da mi neko da link gde sam izvoljevao da mi neko kompletno reši zadatak, a da prethodno nisam ni prstom mrdnuo. [ Farenhajt @ 25.05.2008. 18:51 ] @
Hej, to je bila šala... (Pretpostavljam da ti je poznat taj pojam.) Nije mi bila namera da ti bušim ego, te nema ni potrebe da se rogušiš.
[ Kolins Balaban @ 27.05.2008. 08:52 ] @
nemoj da se ljutis nedeljko, uradit cu ti ja zadatak, samo dok svežem kosu :lol :)
[ sabandijilla @ 30.05.2008. 07:09 ] @
Da li E mora da ima nepraznu unutrasnjost?
[ sabandijilla @ 30.05.2008. 09:20 ] @
Recimo da mora:
E je Lebeg merljiv, pa bi njegova unutrasnja mera bili svi intervali koji sa E imaju zajednickih tacaka (mislim njihova duzina), pa lim kad n->besk. Ako ne bi bilo ni jednog intervala koji je ceo u E onda bi mu unutrasnja mera bila nula, pa bi skup E bio ili nemerljiv ili mere nula. Dakle, E sadrzi neki interval, pa ima unutrasnju tacku recimo x. Onda postoji neka okolina od x : 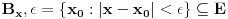 sada 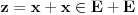 Hocu da pokazem da je z unutrasnja tacka od E+E, tako sto je okolina 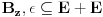 Uzmem proizvoljnu tacku 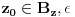 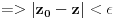 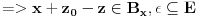 Oznacim je sa 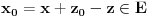 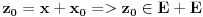 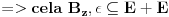 => z je unutrasnja tacka od E+E [ sabandijilla @ 01.06.2008. 17:25 ] @
Da li znas neki primer takvog skupa?
[ Nedeljko @ 06.06.2008. 13:47 ] @
To nije kompaktan skup. No, moze se konstruisati takav skup slicno kao Kantorov, s tim sto ukupna suma sirina izbacenih intervala treba da bude manja od od sirine polaznog intervala iz koga se vrsi izbacivanej.
[ Bojan Basic @ 07.06.2008. 21:37 ] @
Sabandijilla se nigde nije ograničio na kompaktne skupove, već je tražio (makar kako sam ja razumeo) primer bilo kakvog skupa pozitivne Lebegove mere koji nema unutrašnjih tačaka.
[ Sonec @ 28.10.2012. 22:05 ] @
Aj Nedeljko (ako si jos u stanju) napisi to kako si opsti slucaj sve na kompaktne skupove (a bilo bi super ako si u medjuvremenu uradio ceo zadatak (koji je iz knjige Arsenovic/Dostanic/Jocic, jel tako?)).
[ Nedeljko @ 28.10.2012. 23:03 ] @
[ Bojan Basic @ 29.10.2012. 01:02 ] @
Što se samog zadatka tiče, rešenje verovatno najjednostavnije ide preko Lebegove teoreme o gustini. Naime, iz navedene teoreme direktno sledi da postoji
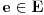 za koje je za koje je 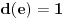 . To znači da možemo odabrati . To znači da možemo odabrati  takvo da je takvo da je 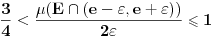 . Dokazaćemo: . Dokazaćemo: 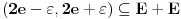 . Pretpostavimo suprotno: neka . Pretpostavimo suprotno: neka 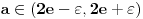 , , 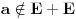 . Neka je, bez umanjenja opštosti, . Neka je, bez umanjenja opštosti, 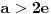 . Tada za svako . Tada za svako 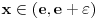 važi važi 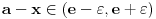 . Kako . Kako 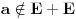 , sledi da , sledi da  i i  ne mogu istovremeno pripadati skupu ne mogu istovremeno pripadati skupu  . Odatle su skupovi . Odatle su skupovi 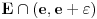 i i 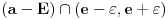 disjunktni, pa važi disjunktni, pa važi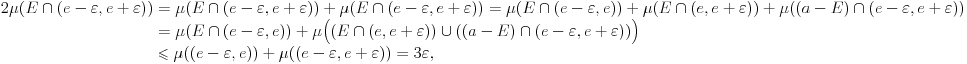 što je u kontradikciji sa izborom  . .Na isti način se dokazuje i da za dva merljiva skupa s pozitivnom Lebegovom merom, 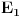 i i 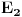 , skup , skup 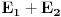 ima nepraznu unutrašnjost. ima nepraznu unutrašnjost.[ Nedeljko @ 29.10.2012. 07:34 ] @
Svaka čast Bojane!
[ Nedeljko @ 28.09.2018. 10:26 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|