Pogledaj teoriju o implicitno zadatim funkcijama, pa se onda javi ako ti ne bude jasno. Ne vredi ovako, kad nećes ni prstom da mrdneš, a očekuješ da neko radi umesto tebe (i to za dž).

Ne tražim da mi neko uradi, već da mi da samo uputstvo za rad. Pročitala sam teoriju, ali očigledno na ovom zadatku ne umem da je primenim.

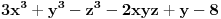
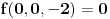
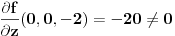
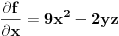
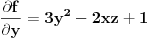
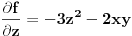
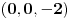
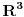
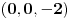
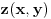
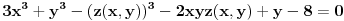
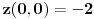
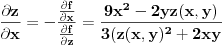
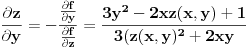
Dakle, za je i , a pritom su parcijalzni izvodi , , neprekidne funkcije u nekoj okolini tacke . (Stavise, neprekidne su na celom .) Stoga u takvoj okolini tacke postoji tacno jedna neprekidna funkcija takva da je i . Ovde se pretpostavlja da je izabrana okolina povezan skup. Stavise, ona je diferencijabilna i za njene parcijalne izvode vazi i . 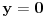E, sad, diferenciranjem ovih formula po i izracunaj i druge parcijalne izvode, pa sve izracunaj za i pa zameni u Tejlorovoj formuli i to ti je to.

Hvala za pomoć, stvarno mi je bila potrebna.