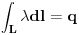
- ukupno naelektrisanje
- naelektrisanje po jedinici duzine

'taraba' cija se povrsina racuna u opstem slucaju ne mora da ide po pravoj liniji, nego moze da krivuda kao kineski zid po nekoj krivoj
liniji u prostoru a visina tarabe se menja zavisno od terena.

Racunanje povrsine takvog zida je primer linijskog integrala funkcije tri promenljive.

Ovaj primer je mozda malo nategnut jer zid (tj. funkcija w = f(x,y,z)) ima vrednosti razlicite od nule bas samo na toj krivoj k(x,y,z), ali
mislim da dobro ilustruje osnovnu ideju.


_{[Ovu poruku je menjao milanche dana 01.06.2008. u 00:54 GMT+1]}

Uprosceno, predstavlja rad sile koji je potreban da se neka materijalna cestica prenese od tacke A do tacke B.

Ako imas krivu u ravni, recimo da su koordinate njenih tacaka x(u), y(u), onda "iznad" krive mozes da posmatras funkciju f kao funkciju dve promenljive z=f(x,y). "Slikovito" integral f(x,y,z)ds po krivoj K ce biti povrsina izmedju krive K i funkcije f.

To sto si dao kao primer nije primer za krivolinijski integral prve vrste vec druge vrste!

Mislim da se moze govoriti o vezi izmedju krivolinijskog integrala I i II vrste posmatrajuci njihove integralne sume i limese tih suma, kao i element luka ds.
A mozda i gresim?