[ Alexandar90 @ 12.06.2008. 16:55 ] @
| Da li neko zna da dokaze teoremu o faktorizaciji polinoma?! (matematickom indukcijom). |
|
[ Alexandar90 @ 12.06.2008. 16:55 ] @
[ miki069 @ 14.06.2008. 17:02 ] @
Ne postoji dokaz indukcijom. Lako se dokazuje preko Bezuovog stava (koji je lak za dokazivanje) i preko "Osnovnog stava algebre" - koji nije lak za dokazivanje.
[ petarm @ 22.06.2008. 13:26 ] @
Za osnovni stav algebre cak ne postoji algebarski dokaz. Vec samo analiticki u okviru kompleksne analize. Samo ne znam dal nije dokazano algebarski il postoji razlog zbog kojeg nikad nece biti ni dokazan algebarski?
[ Bojan Basic @ 22.06.2008. 15:48 ] @
Citat: miki069: Ne postoji dokaz indukcijom. Nije tačno. D’Alamberov dokaz koristi upravo indukciju po stepenu polinoma. Citat: petarm: Za osnovni stav algebre cak ne postoji algebarski dokaz. Vec samo analiticki u okviru kompleksne analize. Ni ovo nije tačno. [ miki069 @ 23.06.2008. 07:08 ] @
Pod "ne postoji dokaz indukcijom" sam mislio na to da ja ne znam za njega.
Prejako je tvrditi da nesta ne postoji a nemati dokaz za suprotno. U svim knjigama iz algebre, koje ja imam, faktorizacije polinoma se dokazuje preko kombinovanja "osnovnog stava algebre" i "Bezouvog stava". Zato sam i luppnuo onu prejaku izjavu "ne postoji dokaz indukcijom". Potrazicu taj D’Alamberov dokaz, ali ga u mojim knjigama, nemam. Bolje je onda tako dokazivati faktorizaciju polinoma, nego koristiti i "osnovni stav algebre", "koji zbog obimnosti dokaza necemo ovde izlagati....". Ostaje supalj dokaz. Hvala Bojane. Pozdrav. [ petarm @ 23.06.2008. 14:15 ] @
Citat: Bojan Basic: Ni ovo nije tačno. Ne znam! Pre oko godinu dana sam pricao o ovome sa Grulom i on mi je rekao da ne postoji algebarski dokaz! Stoga je ovo zanimljivije stoga sto ti je on predavao Galoaovu teoriju! Moguce je da se negde u tom dokazu koriste neka topoloska svojstva!? [ Nedeljko @ 24.06.2008. 14:01 ] @
Citat: Bojan Basic: Ni ovo nije tačno. :) Postoje algebarski dokazi koji od analize traže samo teoremu o srednjoj vrednosti (takav je i upravo pomenuti D’Alamberov) — a ako je i to previše analize, postoji i 100 % algebarski dokaz preko Galoaove teorije. Pa, sad, zavisi sta se smatra algebarskim dokazom. Tu se zapravo misli da se osnovni stav algebre ne moze dokazati samo koriscenjem aksioma uredjenih polja, bez aksioma neprekidnosti. Recimo, polje  zadovoljava sve aksiome uredjenih polja, ali nijedno rasirenje polja zadovoljava sve aksiome uredjenih polja, ali nijedno rasirenje polja  stepena stepena  nije algebarski zatvoreno, (ovde se naravno, pre svega misli na polje nije algebarski zatvoreno, (ovde se naravno, pre svega misli na polje 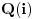 , gde je , gde je  imaginarna jedinica), jer algebarska jednacina imaginarna jedinica), jer algebarska jednacina 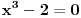 stepena stepena  ima racionalne koeficijente, a nijedan od njenih korena ne pripada nijednom od tih prosirenja. ima racionalne koeficijente, a nijedan od njenih korena ne pripada nijednom od tih prosirenja.Istina je da dokaz osnovnog stava algebre ne zahteva punu snagu aksioma neprekidnosti. Preciznije, aksiome neprekidnosti mozes oslabiti do aksioma realno zatvorenih polja. Drugim recima, za dokaz osnovnog stava algebre dovoljne su aksiome uredjenog polja + svaki pozitivan element polja ima kvadratni koren u polju + svaki polinom neparnog stepena sa koeficijentima iz polja ima bar jedan koren u polju. Prvi dokaz osnovnog stava algebre u realno zatvorenim poljima dao je Gaus, mada ih nije izdvojio kao aksiome jedne teorije. Taj Gausov dokaz se moze naci u udzbeniku algebre profesora Gojka Kalajdzica. Od dva dokaza koja je prilozio, jedan je taj, a drugi je preko Galoaove teorije. Oba koriste samo aksiome realno zatvorenih polja. [ Alexandar90 @ 24.06.2008. 15:29 ] @
Pn(x) = anxn + an-1xn-1 +...+ a1x + a0 = an(xn + an-1'xn-1 +...+ a1'x + a0') = an(x-x0) * Pn-1, pri cemu je x0 nula polinoma Pn(x).
Sada po poslednjoj jednakosti (koja je podvucena) raspisujemo polinome od n-tog do prvog: Pn(x) = (x-x1) * Pn-1(x) Pn-1(x) = (x-x2) * Pn-2(x) . . . P1(x) = (x-xn) * an Zatim se pomnoze leva i desna strana: Pn(x) * Pn-1(x) *...* P1(x) = an * Pn-1(x) * Pn-2(x) *...* P1(x) * (x-x1)(x-x2) *...* (x-xn) Sada se skrati sve sto moze na levoj i desnoj strani i dobije se: Pn(x) = an(x-x1)(x-x2)*...*(x-xn), a to je teorema o faktorizaciji polinoma. Mislim da je ovo dobar dokaz, ispravite me ako sam negde pogresio. Kada budem imao vremena napisacu ga uz pomoc baze i indukcijskog koraka. [ Nedeljko @ 24.06.2008. 17:31 ] @
Teorema o faktorizaciji polinoma tvrdi da se svaki nenula polinom nad bilo kojim poljem moze predstaviti kao proizvod prostih polinoma na tacno jedan nacin do na redosled i pridruzenost cinilaca i nema ama bas nikakve veze sa osnovnim stavom algebre, pa ni Bezuovom teoremom. Dokaz postojanja faktorizacije ide slicno kao ovaj gore navedeni, s tim sto nerastavljivi polinomi u opstem slucaju mogu biti bilo kog stepena. Naravno, treba dokazati i jedinstvenost faktorizacije. No, nije mi jasno zasto postavljac teme nije konsultovao svoj udzbenik, nego hoe da mu neko ovde prekucava knjigu.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|