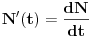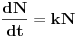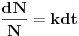[ igac @ 16.06.2008. 23:31 ] @
| trazio rjesenje, nazalost bezuspjesno pa se opet javljam ovde poslije duzeg perioda... :) uglavnom zadatak je: "pomocu tejlorovog razvoja procijeniti kolika greska nastaje prilikom racunanja povrsine jednakokrakog trougla, ako se stvarna vrijednost kraka 3.1m zamijeni duzinom od 3m a ugao izmedju krakova koji je 33stepena zamijeni sa 30stepeni?" e sada meni je ideja bila da uzmem tejlorov razvoj dvije promjenljive f(x,y) gdje je f(x,y) funkcija koja predstavlja povrsinu ( povrsina = x^2*sin(y)/2 ) ali prvo nisam mogao naci taj tejlorov razvoj a kada sam i nasao nisam bas siguran kako ga iskoristi... da je bilo npr 30stepeni a mijenja se 3.1m sa 3m pretpostavljam da bi islo nesto ovako p(3) = p(3.1) + p'(3.1)*(3-3.1) + 1/2! * p"(3.1)*(3-3.1)^2 + ... je l' tako? i koliko clanova razvoja bih uzeo uopste? i naravno pitanje kako to ide za 2 promjenljive (i krak i ugao se mijenjaju)? evo ako neko naleti da zna i drugi zadatak: "broj bakterija N u nekoj koloniji povecava se po Maltusovom modelu N'(t) = k*N(t) gdje je k neka konstanta a vrijeme t se izrazava u satima. Ako se zna da je u pocetku bilo 2000 bakterija a nakon 3 sata 2200 odrediti koliko ce ih biti nakon 6 sati." nikad cuo za taj maltusov model ali ako je k konstana i za 3h nastane 200 bakterija onda je l' za 6h nastane 400 bakterija?:) |