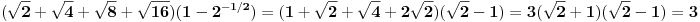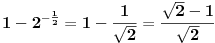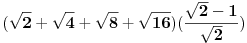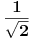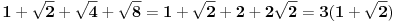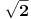[ Bootta11 @ 18.06.2008. 10:31 ] @
|
[ Bootta11 @ 18.06.2008. 11:58 ] @
Hvala na odgovoru. Da li bi neko mogao da pojasni ovaj zadatak(npr odakle se pojavi 1 u prvoj zagradi, kako su uprosceni svi koreni u prvoj zagradi itd....)
[Ovu poruku je menjao Bootta11 dana 18.06.2008. u 13:38 GMT+1] [ Bootta11 @ 18.06.2008. 13:11 ] @
Evo vec 3 sata razbijam glavu sa ovim zadatkom. Odgovor koji je postavio Nedeljko je tacan ali ne kontam na koji nacin je uprostio ovaj izraz.
[ hakurik @ 18.06.2008. 13:51 ] @
[ Bootta11 @ 18.06.2008. 14:09 ] @
Hvala na pomoci, sad mi je mnogo jasnije. I ako vam jos nije tesko da mi napisete koji prog koristite da napisete ove zadatke sa svim ovim korenima i stepenima.
[ hakurik @ 18.06.2008. 14:35 ] @
izmedju tagova "[A]" i "[/A]" pises formulu. Umjesto slova A pises "tex", bez navodnika. klikni na neku od navedenih formula, pa ces vidjeti kao kod izgleda.
[Ovu poruku je menjao hakurik dana 18.06.2008. u 15:45 GMT+1] [ zzzz @ 18.06.2008. 14:38 ] @
Klikni na neku formulu pa ćeš vidjeti šta se krije iza.Samo je taj tekst još uokviren
tagovima (tex)----------(/tex).Ove zagrade treba da su [ ].Pročitaj prvu temu na ovom forumu," sve o latexu" pa ćeš ovladati ovim programom. [ Bootta11 @ 18.06.2008. 14:42 ] @
Ok mislim da sam skontao. Hvala svima na pomoci
[ Daniel011 @ 18.06.2008. 17:32 ] @
[ Nedeljko @ 22.06.2008. 07:58 ] @
[ petarm @ 22.06.2008. 13:02 ] @
Citat: Daniel011: Ovaj zadatak je moguće rešiti i preko sume geometrijskog reda, nije loše znati i taj način za slučaj kada ima više sabiraka: 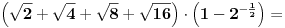 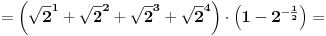  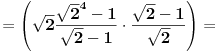 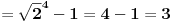 Mozda bi trebalo reci sume geometrijskog niza jer je suma geometrijskog reda 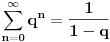 za 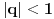 [ Daniel011 @ 23.06.2008. 01:01 ] @
Da, u pravu si.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|