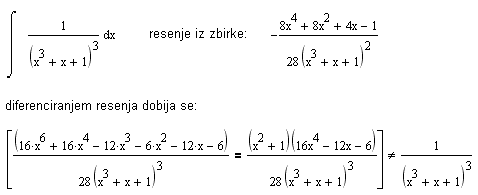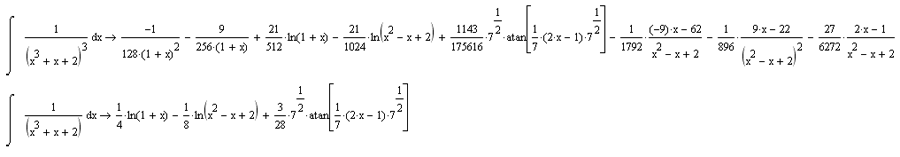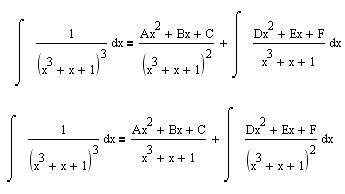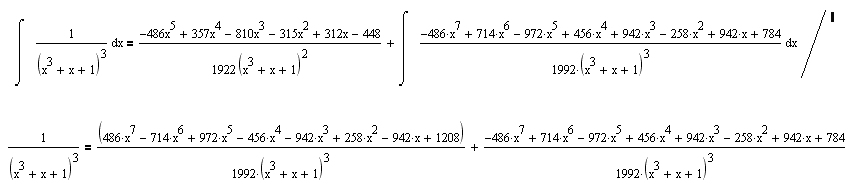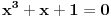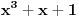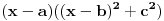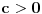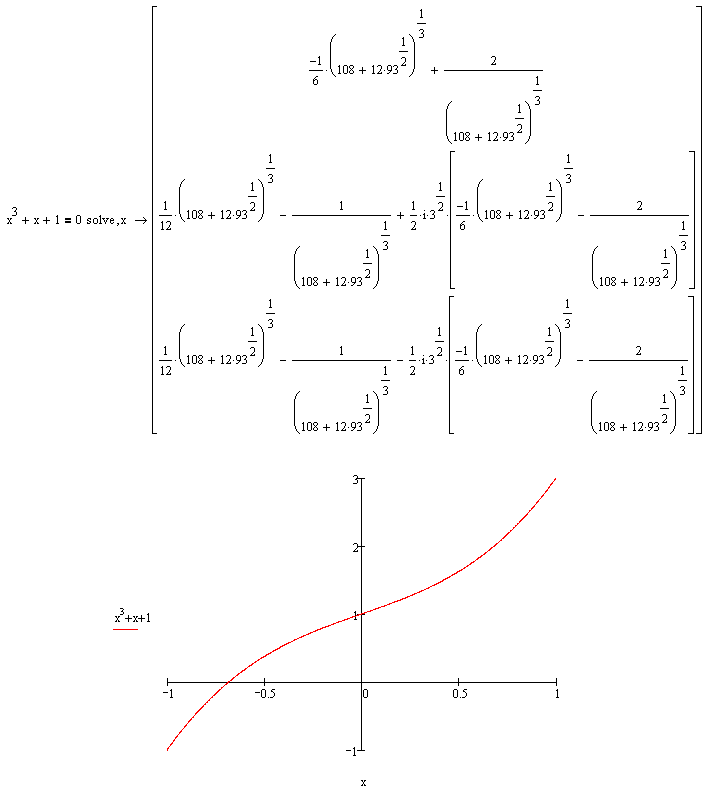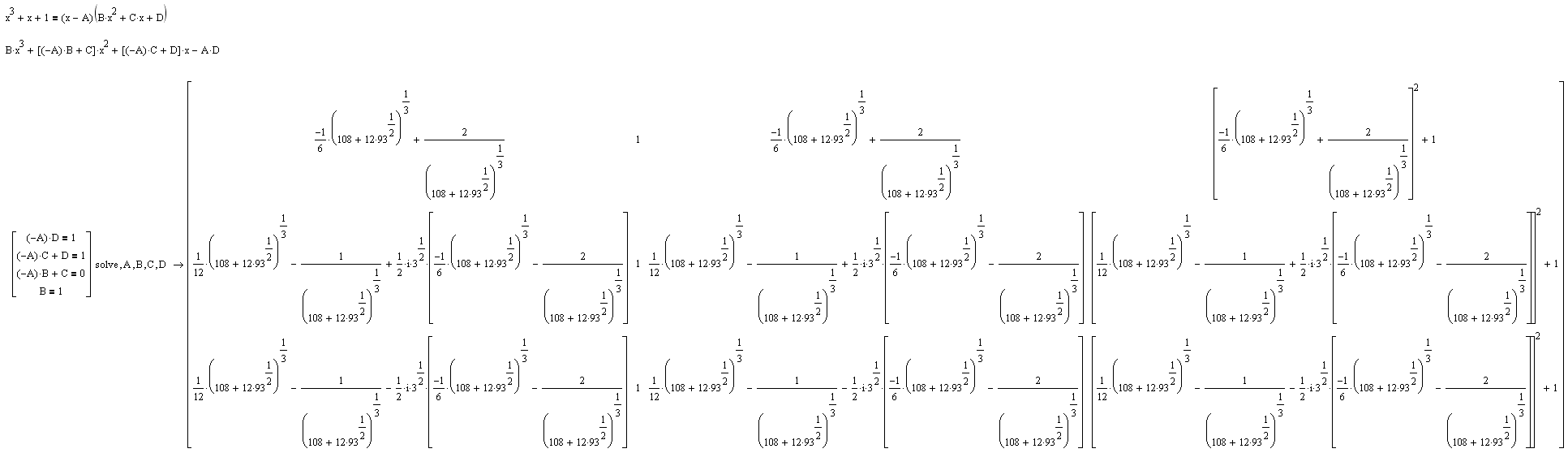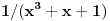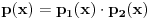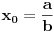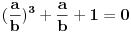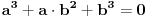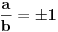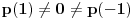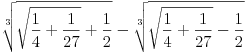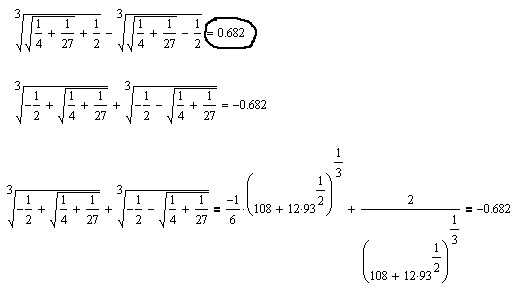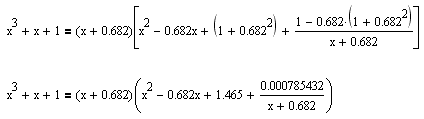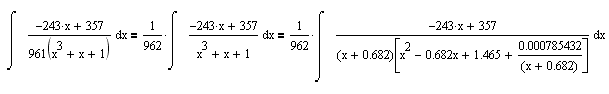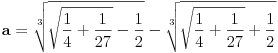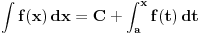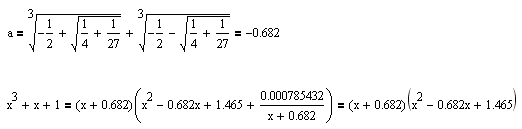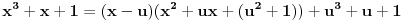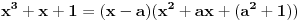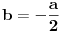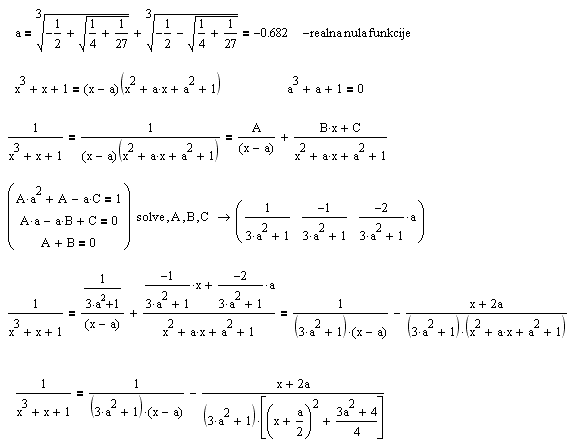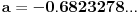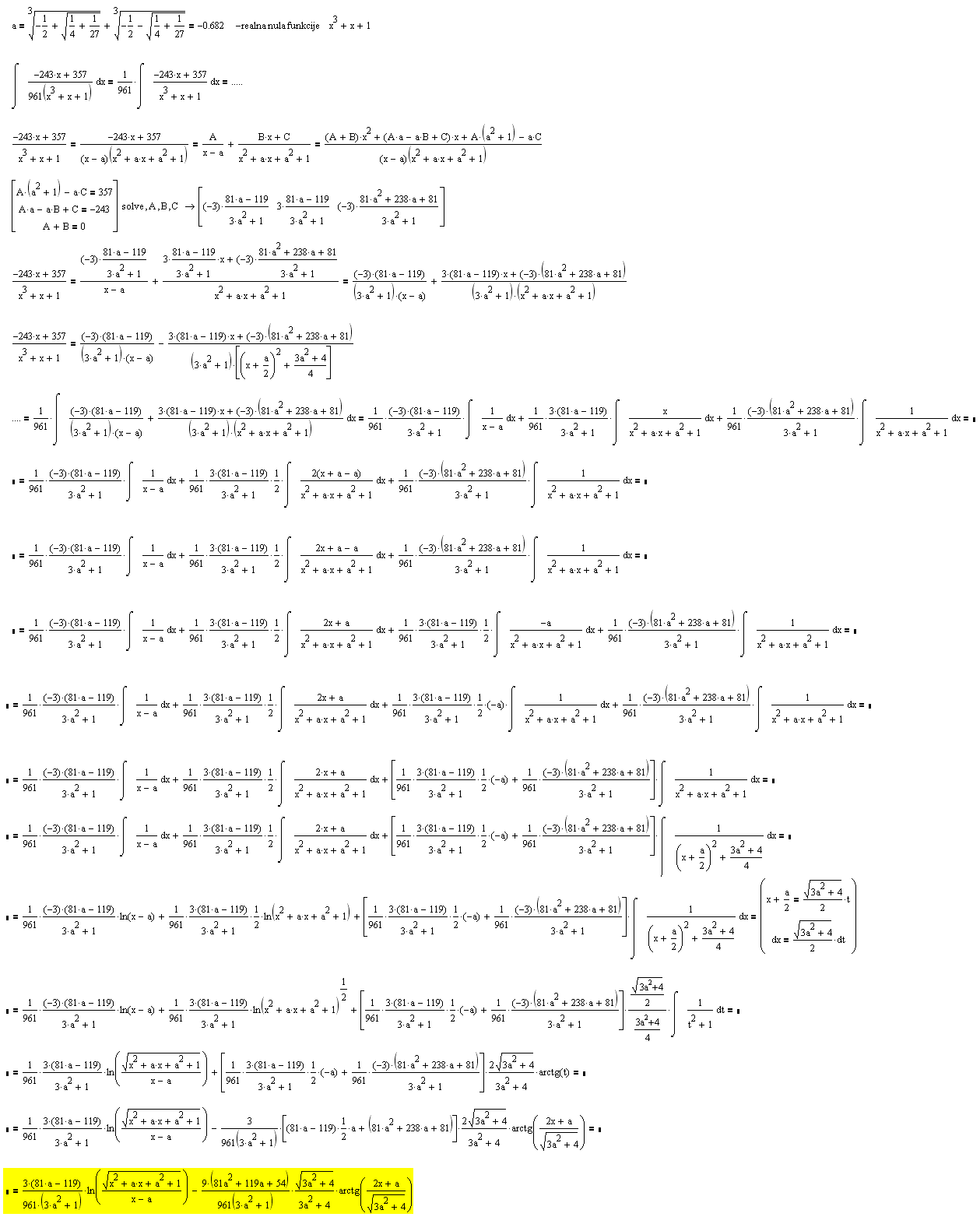|
|
[ igorpet @ 20.06.2008. 12:13 ] @
|
| Imam problem da resim jedan integral iz zbirke Uscumlic, Milicic (br. 3423):
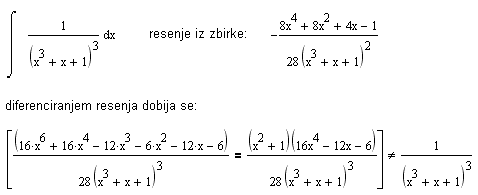
Resenje iz zbirke ne odgovara zadatku, i sumnjam da je postavka losa.
Nema puno gresaka u zbirci, ali sam ipak primetio neke greske u nekoliko zadataka pa sam posle duzeg vremena posumnjao da je i ovde greska.
Obicno je greska u znaku (+,-) ili u stepenu.
Pokusavao sam na razne nacine da resim, ali ne ide.
Da li se ovaj integral uopste moze resiti u domenu elementarnih f-ja?
Ima li ko ideju kako bi zadatak mogao da se resi, ili ako je greska u postavci kako bi trebalo da izgleda dobro postavljen zadatak. |
[ sanja2010 @ 20.06.2008. 16:42 ] @
Eto ti... taman sam potisnula Uscumlica kao ruzno secanje... :)
Ima gresku taj zadatak, mathematica kao resenje vraca formulu sa slicice.
Nadji izvod resenja pa ces videti kako izgleda pravi integral. Koliko se secam, nije nista mnogo slicno datom.
Btw, ta zbirka je uzas zivi, puna gresaka sto u zadacima sto u resenjima.
[ igorpet @ 22.06.2008. 23:43 ] @
Niko nema ideju kako bi mogo da se resi ovaj integral? (ako uopste moze da se resi)
Vidim da je integral ponovljen i u dokumentu http://web.math.hr/nastava/analiza/files/ch2_3.pdf pa rekoh da mozda ima resenje (nisu ga valjda samo prepisali, bez provere). [ sanja2010 @ 23.06.2008. 00:07 ] @
Ja ti poslah kako izgleda resenje :) Koliko ja znam, ne moze da se resi, a da dobijes nesto lepo... posebno ne moze da dobijes njihovo resenje.
[ igorpet @ 23.06.2008. 00:15 ] @
Citat: sanja2010: Ja ti poslah kako izgleda resenje :) Koliko ja znam, ne moze da se resi, a da dobijes nesto lepo... posebno ne moze da dobijes njihovo resenje.
Da, video sam, i ja sam slicno resenje dobio u mathcadu, ali i za jos neke teze integrale dobijao sam slicna resenja u mathcadu (kao nemaju resenje) a u stvari imali su resenja u domenu elementarnih f-ja samo sto ih program nije prepoznao.
Mat. Programi nisu pouzdano resenje da se integral ne moze resiti.
A resenje ne mora biti ovo iz zbirke, interesuje me da li se uopste moze resiti i kako! [ miki069 @ 07.07.2008. 21:57 ] @
Polinom: X^3 + X + 1 ima samo jednu realnu nulu X1 na intervalu (-1,0).
Ona je iracionalna i tu je kraj normalnog resavanja integrala racionalnih funkcija.
Aj probaj da nije bio polinom: X^3 + X + 2 koji ima nulu X1 = -1.
Ne da radis integral. Smorno je mnogo.
Stavi u resenje (X^3 + X + 2 ) umesto (X^3 + X + 1) pa onda probaj izvod.
Mada to gubi smisao da ti otkrivas tekst zadatka u tako eminentnoj zbirci.
Koja ima beskonacno izdanja.
Ja imam beskonacno po redu izdanje i isti je tekst zadatka - pogresan (ili je resenje pogresno??).
Za ovaj sa (X^3 + X + 1)^3 tvrdim 99,99% da ne moze da se uradi.
Ne iz mathcada. Vec iz iskustva.
Mada ostaje 0,01%.
Kao sto ti rece.
Nikad se ne zna 100%.
Zbunjuju me koske od zadataka iza tog, u zbirci, koje se sve urade bez problema iako su im polinomi u imeniocu jos sugaviji od (X^3 + X + 1)^3.
Tipa nema ni jednu realnu nulu, al moze.
Ovde ubija vise 1 u brojiocu.
1 = (3*X^2 + 1) - 3*X^2.
Podelis na 2 integrala.
Al onaj drugi ni makac...???
Pozdrav
[Ovu poruku je menjao miki069 dana 07.07.2008. u 23:08 GMT+1]
[ igorpet @ 08.07.2008. 11:33 ] @
Miki, probao sam 101 nacin (figurativno receno) da resim u originalu (1/(X^3 + X + 1)^3) i njega nije moguce resiti.
E sad najvise me je zbunilo to sto je isti integral dat kao vezba na nekom od fakulteta (ima link) i pomislio sam da ne bi neko samo tek tako prepisao zadatak a da ga prethodno nije resio, mada izgleda da je bas tako bilo.
Inace zbirka je odlicna, i integrali su mozda jaci nego u drugim zbirkama ovog ranga, i bilo je stvar principa sto ne mogu da resim zadatak.
Inace imam prilicno iskustva sa integralim, pa je proradio inat, no bice da je problem u postavci (a resenje deluje tako da se sasvim uklapa u postavku, barem na prvi pogled).
Za varijantu (X^3 + X + 2 ) resenje postoji. I MathCad ga je prepoznao:
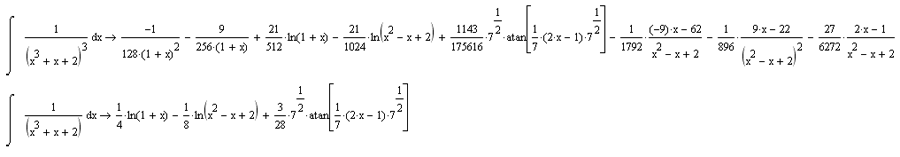
I bas me interesuje da li je resenje toliko omanulo u odnosu na postavku ili ipak ima neka "caka" kao sto i ti rece.
Ili i postavka i resenje imaju gresku, pa je onda jako tesko predvideti sta je autor hteo "reci". [ miki069 @ 08.07.2008. 15:14 ] @
I mene najvise zbunjuje sto iza njega uz zbirci ima, na prvi pogled, vecih koski od njega, al se urade uz manje vise problema.
I kod mene je inat u pitanju.
Kao integral racionalne f-je je kraj price.
I sva muvanja na taj fazon mislim da nemaju sanse.
Probacu jos kombinacije (sulude) x=sint ili x=cost ili x=tgt ili x=ctgt ili x=sinht....
Ako uradim javljam.
[Ovu poruku je menjao miki069 dana 08.07.2008. u 22:17 GMT+1]
[ adnanK @ 14.07.2008. 14:01 ] @
Koristi metod Ostrogradskog i moguce je rijesiti integral   [ igorpet @ 15.07.2008. 00:18 ] @
Citat: adnanK: Koristi metod Ostrogradskog i moguce je rijesiti integral :) :)
Koristio sam metodu Ostrogradskog i do sada ali ne mogu da resim.
Kako god da postavim ne mogu da dobijem koeficijente tj. sistem nema resenje.
Jel moze malo detaljnija pomoc?
Ja sam postavljao zadatak ovako (na dva nacina ali ne ide ni u prvom ni u drugom slucaju):
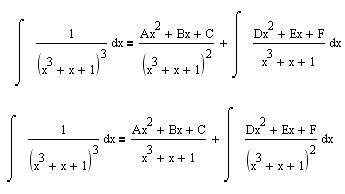
Jel ja gresim negde?
Ovako nekako se valjda postavlja zadatak kad funkcija ispod razlomacke crte ima visestruke korene, ali ova nema visestruke korene.
Zato me malo zbunjuje kako ovo uraditi metodom Ostrogradskog !!??
[Ovu poruku je menjao igorpet dana 15.07.2008. u 01:33 GMT+1][ igorpet @ 27.07.2008. 23:07 ] @
Evo jos nekih stvari u vezi ovog zadatka koje sam uspeo da pribavim.
U jednoj ruskoj zbirci nasao sam ovaj zadatak kao i resenje (konacno).
U njoj zadatak glasi: naci racionalni deo integrala, sto znaci da integral nema konacno resenje.
E sad, mene interesuje kako naci samo ovaj racionalni deo, jer ja nijedan primer nisam radio niti sreo zadatak poput ovoga.

Da li bi to trebalo ovako da izgleda?
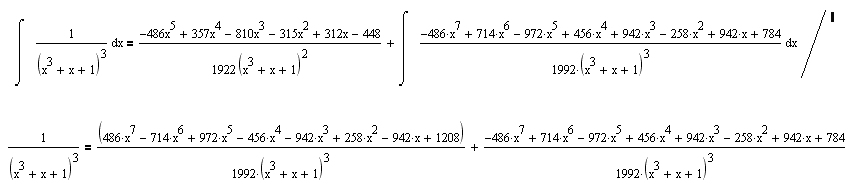 [ igorpet @ 28.07.2008. 18:34 ] @
Pa, evo posle vise od 8 meseci palo je i resenje integrala koji me je namucio.
Naravno nisam mislio samo na zadatak svo ovo vreme, ali prilicno mi je vremena (slobodnog) potrosio, pa mi je resenje jos sladje a narocito sto sam do njega dosao sam.
Necu da delujem nezahvalno, ali ipak cu morati da se zahvalim samo samom sebi  (i knjigama koje sam koristio).
Da li je zadatak bio toliko tezak ili ljudi nisu bili dovoljno motivisani da se pozabave problemom ne znam, ali sem adnanK koji je slucajno ili namerno pogodio metod za resavanje druge konstruktivne pomoci nisam imao.
(Sve gore navedeno shvatite samo kao malo opsirnije razmisljanje na glas - molim Vas nista vise od toga nije u pitanju)
Ipak je bio Ostrogradski u pitanju!!!
A do ovog resenja sam dosao konsultujuci pa barem jedno 10 eminentnih Ruskih zbirki i knjiga.
No, kad vidite resenje videcete da i nije nesto bogzna kako tesko 
A cela poenta je bila u tome sto ja nisam znao da pravilno postavim resenje metodom Ostrogradska, inace resenje bi palo jos davno ali onda verovatno mnogi ne bi saznali za resenje ovog zadatka, tako da i to ima nekih svojih prednosti.
Pa evo i resenja:
 [ Nedeljko @ 29.07.2008. 17:56 ] @
Izvini, ali ja ovde i dalje ne vidim resenje integrala. Treba integraliti još onaj ostatak. On se može izraziti preko rešenja jednačine 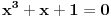 (jedno je realno i dva su konjugovano kompleksna). [ igorpet @ 29.07.2008. 18:11 ] @
Citat: igorpet: U jednoj ruskoj zbirci nasao sam ovaj zadatak kao i resenje (konacno).
U njoj zadatak glasi: naci racionalni deo integrala, sto znaci da integral nema konacno resenje.
U pravu si Nedeljko ali radi se o tome da ovaj drugi integral nema racionalno resenje, tako da je konacno resenje ovakvo.
Radi se o tome sto u Uscumlicu nije korektno data postavka zadatka.
Zadatak bi trebao da glasi: Naci racionalni deo integrala jer ovaj integral nema resenje u oblasti realih funkcija ali zato deo tog integrala ima.
Ti ako smatras da moze drugacije ... Voleo bih da vidim resenje  [ Nedeljko @ 30.07.2008. 09:03 ] @
Napiši 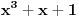 kao 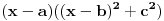 , 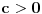 , pa ćes moći da ga rešiš. Uzgred, mogu se i izrašunati  rešavanjem kubne jednačine 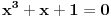 . [ igorpet @ 30.07.2008. 12:08 ] @
Citat: Nedeljko: Napiši 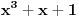 kao 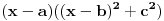 , 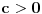 , pa ćes moći da ga rešiš. Uzgred, mogu se i izrašunati 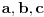 rešavanjem kubne jednačine 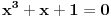 .
OK Nedeljko.
Ova funkcija ima jednu realnu nulu, i stvarno bi mogla da se faktorizuje sa (x-a) ali nesto mi ne ide bas.
Evo resenje ove kubne jednacine:
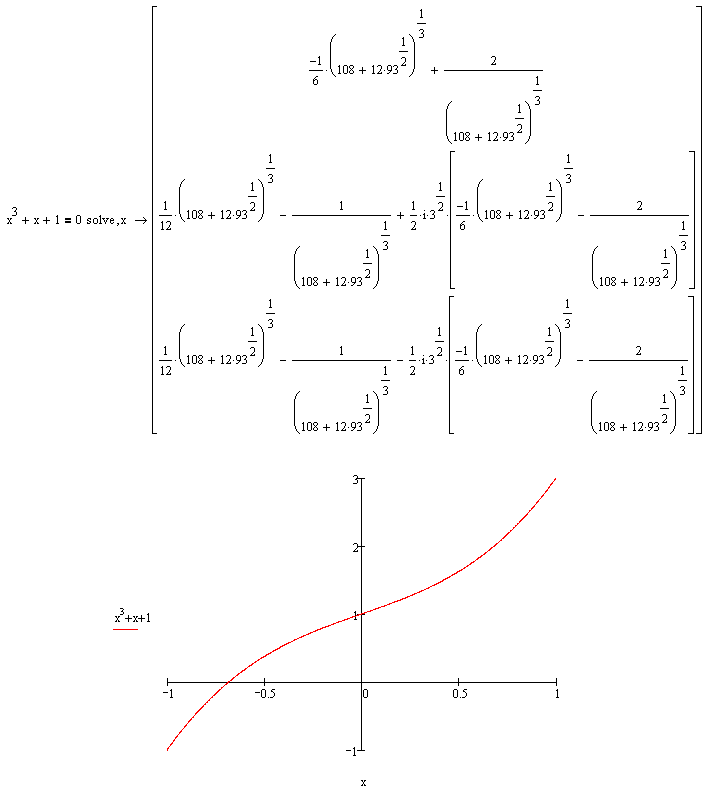
A evo i vrednosti za koeficijente:
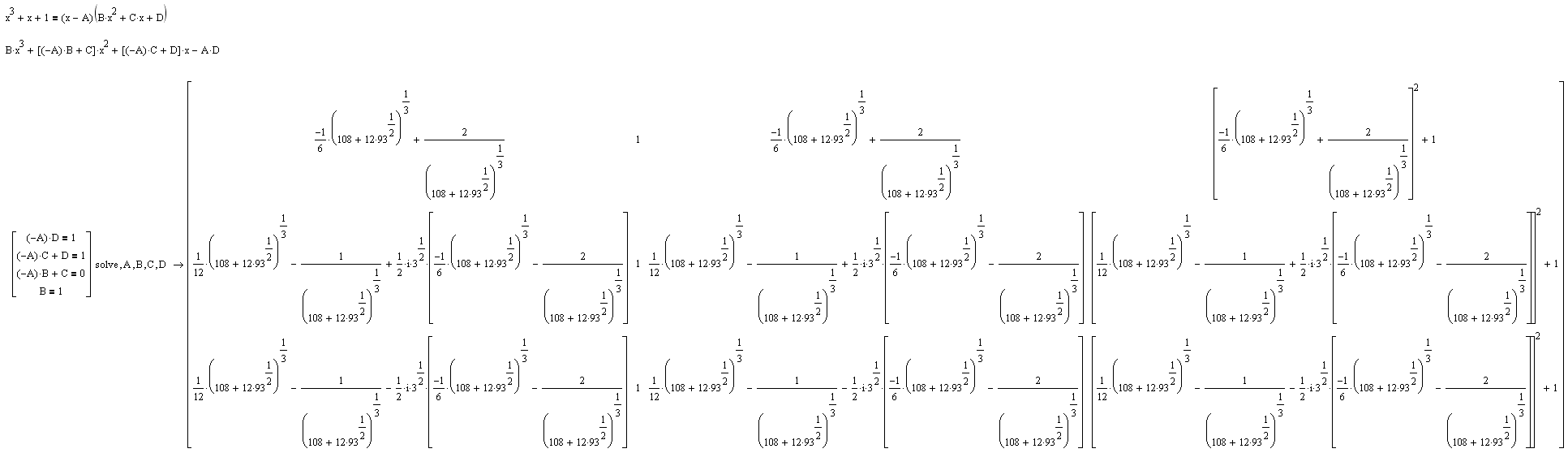
Kako sada?
Znam kako ide, ali ove vrednosti za koeficijente me zbunjuju.
Da li se 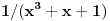 uopste moze rastaviti na dva prostija razlomka? [ igorpet @ 30.07.2008. 13:19 ] @
O problemu ovog polinoma bilo je reci i na temi:
http://www.elitesecurity.org/t...jivost-polinoma-treceg-stepena

Citat: KPYU: Ako želimo da rastavimo ovaj polinom nad Q[x], to znači da želimo da bude
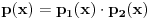 gde su p 1 i p 2 ne-konstantni polinomi iz Q[x]. To znači da jedan od njih mora da bude linearan, a to opet znači da P mora da ima bar jednu racionalnu nulu. Neka je to x 0. Dakle neka je
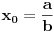
Tad mora biti 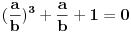 , tj
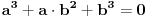 gde je b broj, a a ceo broj. Sad vidimo da a deli b, i da b deli a. Onda je 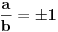
Ali 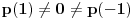
Zaključak: ne postoji racionalna nula, dakle p(x) nije rastavljiv.
Da li to znaci da je svaki pokusaj rastavljanja polinoma 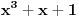 uzaludan? [ Nedeljko @ 30.07.2008. 15:19 ] @
To znači da je svaki pokušaj rastavljanja tog polinoma nad poljem racionalnih brojeva uzaludan, ali ne i nad poljem realnih briojeva. Zar ne znaš kako se rešava opšta jednačina trećeg stepena? Realno rešenje ove jednačine je 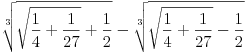 . [ igorpet @ 30.07.2008. 15:54 ] @
Citat: Nedeljko: ... Zar ne znaš kako se rešava opšta jednačina trećeg stepena? ...
Valjda Kardanove formule (nego brze mi ide kada mi odradi program nego kada ja sam racunam  )
Mozda nekom zatreba:
Citat:
Kardanove formule nogu se dobiti na sledeći elementarni način.
Data je jednačina trećeg stepena u opštem obliku:
ax3 + 3bx2 + 3cx+d=0 (1)
Ako stavimo x=y - b/a jednačina (1) se svodi na oblik
y3+3py+2q=0 (2)
gdje je p=c/a - b2/a2 i 2q=2b3/a3 - 3bc/a2 + d/a
Uvodeći novu nepoznatu u pomoću jednakosti y=u - p/u
i unoseći taj izraz u (2), dobijamo
u6 + 2qu3 - p3=0 (3)
odakle se dobija
u3= -q ± (q2+p3)
Prema tome
y= (-q ± (q2 + p3)1/2)1/3 - p((-q ± (q2 + p3)1/2)-1/3
Ako se brojilac i imenilac drugog sabirka pomnože sa
(-q -(± (q2 + p3)1/2))1/3
imajući u vidu da je izraz za u simetričan u odnose na znake + i -, konačno se dobija
y= (-q + (q2 + p3)1/2)1/3 + (-q - (q2 + p3)1/2)1/3
(Proizvod kubnih korijena u posljednjem izrazu jednak je p.) To je Kardanova formula.
Dakle, vrlo jednostavnom zamjenom, kubna jednačina (2) se svodi na kvadratnu jednačinu (3) po nepoznatoj u3.
Nego malo si permutovao ove razlomke u resenju pa si omanuo za jedan -
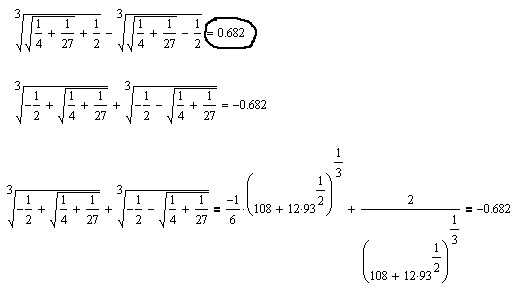 [Ovu poruku je menjao igorpet dana 30.07.2008. u 17:21 GMT+1]
[Ovu poruku je menjao igorpet dana 30.07.2008. u 17:21 GMT+1][ igorpet @ 30.07.2008. 16:51 ] @
I ako mi na trenutak ostavimo po strani racionalne brojeve, prilikom faktorisanja ove funkcije dobijam:
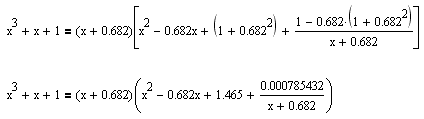
Cemu ovo sluzi a da moze biti korisno?  [ Nedeljko @ 31.07.2008. 08:11 ] @
Polinom 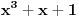 se moze podeliti sa  , pri cemu ce kolicnik biti izrazen preko  . Potom se mogu resavanjem kvadratne jednacine izraziti  preko  . Onda mozes resiti integral preko  , (odnosno preko  obzirom kako su izrazeni 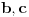 ), da bi na kraju mogao da se puvas da imas tacno resenje integrala. Ako treba da saljes raketu na jupiter, svakako ces imati neki odredjen integral, jer konacan rezultat mora biti broj, a za to su ti dovoljne numericke aprokcimacije brojeva 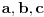 ili integral numericki izracunat na neki drugi nacin. Ne znam da se neko ovajdio od tacnih resenja ovakvih jednacina. [ igorpet @ 31.07.2008. 08:50 ] @
Citat: Nedeljko: Polinom 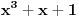 se moze podeliti sa  , ...
Ovaj polinom se moze podeliti sa  ali ne bez ostatka.
Ne moze se ovaj polinom podeliti realnom nulom i da nam kolicnik bude bez ostatka, mislim da je to glavni problem.
I zbog toga u kolicniku nema kvadratne jednacine, i ne moze se razloziti na dva prostija razlomka.
Zato ja smatram da ovaj integral nema resenje u oblasti realnih funkcija.
A i isprobavao sam razne druge tehnike, i takodje ne ide, ali ne tvrdim da nema resenja, vec samo smatram da se ne moze resiti.
Da li Nedeljko ti tvrdis suprotno? da se moze resiti
Ako se integral resi licno cu pisati Kudrjavcevu i Kutasovu, a i recezentima akademicima Iljinu i Nikoljskom, da njihova cenjena zbirka ima gresku 
A o raketama, Jupiteru i odredjenim integralima cemo u nekoj drugoj poruci.
Ovde je problem u neodredjenom integralu, i nemam u planu skorije slanje rakete bilo gde ali to ne znaci da ne treba da se interesujem za integrale, zar ne? 
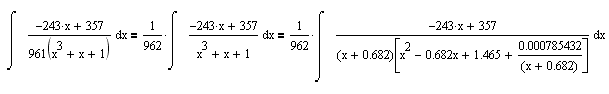
Citat: Nedeljko:... Ne znam da se neko ovajdio od tacnih resenja ovakvih jednacina.
I zasto mislis da ovo radim da bi se ovajdio?
Ima valjda nesto i u licnoj satisfakciji a ne samo u novcu! [ Nedeljko @ 31.07.2008. 09:58 ] @
Citat: igorpet: Ovaj polinom se moze podeliti sa  ali ne bez ostatka.
Polinom 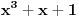 se može podeliti sa  bez ostatka ako i samo ako je  koren polinoma 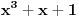 , tj. ako i samo ako je  . U opštem slučaju se ostatak izražava kao polinom deljiv sa 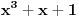 po  , tako da ako si izabrao 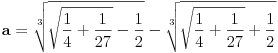 , onda ostatak možeš mirne duše formalno da odbaciš.
Citat: igorpet: Zato ja smatram da ovaj integral nema resenje u oblasti realnih funkcija.
U skupu realnih funkcija na nekom intervalu postoji neodređeni integral bilo koje neprekidne funkcije na tom intervalu. Izražava se kao 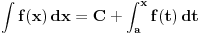 gde je  neprekidna funkcija na intervalu  i  proizvoljna tačka intervala  . No, svaka racionalna funkcija ima neodređeni integral čak i u skupu elementarnih funkcija.
Citat: igorpet: licno cu pisati Kudrjavcevu i Kutasovu, a i recezentima akademicima Iljinu i Nikoljskom, da njihova cenjena zbirka ima gresku
Retke su knjige bez grešaka.
Citat: igorpet: I zasto mislis da ovo radim da bi se ovajdio?
Ima valjda nesto i u licnoj satisfakciji a ne samo u novcu!
A gde sam ja to tvrdio? Samo sam odgovorio na pitanje onako kako je ono postavljeno. [ igorpet @ 31.07.2008. 11:32 ] @
Citat: Nedeljko: ... tako da ako si izabrao 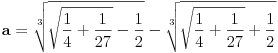 , onda ostatak možeš mirne duše formalno da odbaciš.
Nedeljo jesi ti poceo da me zezas? A znas da nije lepo zezati mladje od sebe , Nedeljko, Nedeljko  (ja sam '74)
Jel ti kazes (i stvarno mislis), da ja onaj ostatak samo odbacim i picim dalje?
I da je:
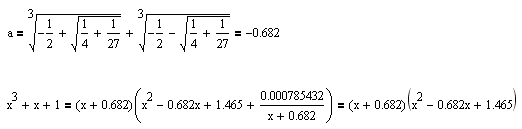
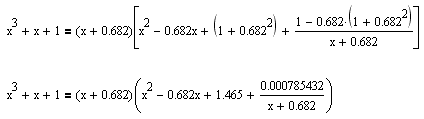
Jes da je ostatak mali, i da ja nisam formalista ali bre ... ipak mi nije jasno kako.
E ovako! Ja se predajem.
Znaci ne tvrdim ali smatram da se ovaj Integral ne moze resiti (u skupu realnih funkcija).
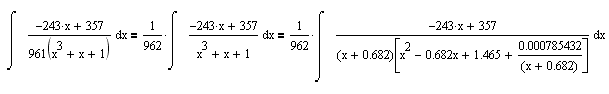
Ti ako smatras ili tvrdis da moze, bilo bi lepo da nam to i dokazes.
Dovoljno je da samo das resenje tog integrala (ne mora postupak).
Nema tu tako mnogo posla (ako znas kako treba da se resi), pa bi bilo lepo da nam predocis.
Ne moraju nikakva dodatna objasnjenja ili bilo sta sto oduzima vreme.
I da, jedini uslov je da resenje bude tacno, jer netacnih imam nekoliko
Rukavica je bacena! Jel prihvatas izazov?  [ Nedeljko @ 31.07.2008. 11:59 ] @
Citat: igorpet: Nedeljo jesi ti poceo da me zezas?
Ni najmanje.
Citat: igorpet: Nedeljko, Nedeljko :) (ja sam '74)
Rodjen sam 31.12.1973. oko 8:20 ujutro ako te baš zanima.
Citat: igorpet: Jel ti kazes (i stvarno mislis), da ja onaj ostatak samo odbacim i picim dalje?
Da. Naravno, koristi tačnu, a ne približnu vrednost realnog korena. To je iracionalan broj, koji samim tim ne može biti jednak  . Dobio si mali ostatak zato što si koristio približnu (a ne tačnu) vrednost za  . Tačna vrednost je zapisana izrazom u kome učestvuju koreni. Dakle, za ma koje  važi:
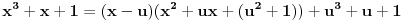 .
Zameni  sa  i dobićeš
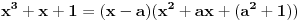
jer je  . Dalje je 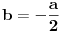 ,  . Batali numeriku (jer ovde nije primenljiva) i koristi oznake 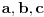 . [ igorpet @ 31.07.2008. 14:48 ] @
Ma bre Nedeljko jel znas da si izgleda 100% u pravu (sem realne nule koja je ipak -0,682  ipak pogledaj grafik funkcije)
Mada je to sigurno zbog toga jer si u odnosu na mene u prednosti za 11 meseci i 13 dana.
Verovatno bih se i ja setio ovoga za 11 meseci i 13 dana 
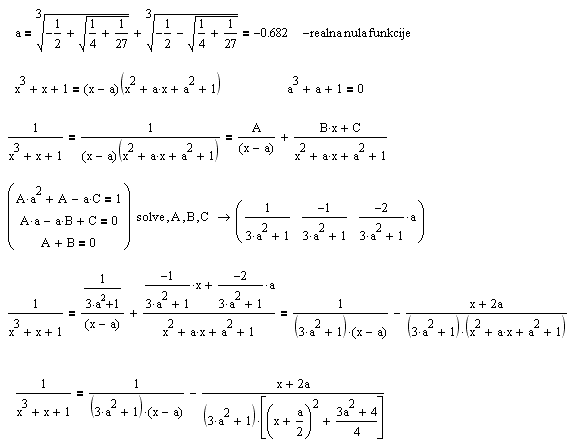
Kasnije cu da odradim i ostalo!
Ti si dovoljno pomogo (za sada  ) [ Nedeljko @ 31.07.2008. 14:58 ] @
Citat: igorpet: Ma bre Nedeljko jel znas da si izgleda 100% u pravu (sem realne nule koja je ipak -0,682 :) ipak pogledaj grafik funkcije)
Ama, ne sumnjam ja da je ta nula (po mom kalkulatoru  ) priblizno jednaka  , ali nije jednaka toj vrednosti, kao sto  nije  . Konstanta  je iracionalan broj i ne moze se prikazati tacno sa konacnim brojem decimala. [ igorpet @ 31.07.2008. 18:10 ] @
Citat: Nedeljko: Ama, ne sumnjam ja da je ta nula (po mom kalkulatoru 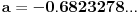 ) priblizno jednaka  , ali nije jednaka toj vrednosti, kao sto  nije 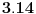 . Konstanta  je iracionalan broj i ne moze se prikazati tacno sa konacnim brojem decimala.
Ma bre razumeli smo se potpuno (posle jedno 10 poruka) nego sam hteo reci da je realna nula sa leve strane x-ose i da je vrednost negativna jer ova tvoja vrednost 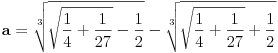 je a=+0.682 a treba biti a=-0.682 jer si ti malo permutovao vrednosi pa ti je vrednost +0.682 i moja primedba se samo na to odnosima u vezi realne nule  (i ja sam zaokruzio na 3 decimale cisto simbolicki, podrazumeva se da to nije tacna vrednost vec samo priblizna).
A jel si ti ove formule znao napamet?
Vidim da si omanuo dva puta do sada (vrlo male greske) i bas me interesuje da li si se ti ovom funkcijom bavio do sada ili si ovo izvodio?
Pitam cisto informativno. Jel ti je matematika u sklopu profesionalnih obaveza? [ igorpet @ 31.07.2008. 20:23 ] @
Evo resenja jednog integrala sa dokazom resenja za koji sam takodje smatrao da se ne moze resiti (a to su smatrali i matematicki programi koje sam koristio) a ova "jednostavna" transformacija nam to omogucava.
 [ Nedeljko @ 01.08.2008. 08:25 ] @
Citat: igorpet: Vidim da si omanuo dva puta do sada (vrlo male greske) i bas me interesuje da li si se ti ovom funkcijom bavio do sada ili si ovo izvodio?
Koja dva puta? Valjda samo prvi put. Kardanove formule retko koristim i uvek ih izvodim (za svaki slučaj). [ igorpet @ 01.08.2008. 08:40 ] @
Citat: Nedeljko: Koja dva puta? Valjda samo prvi put. Kardanove formule retko koristim i uvek ih izvodim (za svaki slučaj).
U prvoj formuli male permutacije vrednosti a u drugoj treba + a ne - pod korenom , ali su ove greske nebitne, bila je bitna ideja, i pomislio sam da si se bavio skorije ovom funkcijom pa da su ti ove formule poznate.
I ja Kardanove formule koristim jako retko (skoro pa nikad) ali dovoljno je znati za njih pa kad zatrebaju ... [ igorpet @ 04.08.2008. 00:09 ] @
Zahvaljujuci Nedeljku uspesno je resen i drugi deo integrala.
Uz ovu transformaciju funkcije u imeniocu resenje je prilicno jednostavno. Ni ovaj integral nece vam resiti neki od matematickih programa.
Za sada samo resenje drugog integrala a kad stignem ovih dana provericu da li je ukupno resenje ogovarajuce (nacicu i izvod).
Evo i detaljnog resenja: (mozda i detaljnije nego sto je neophodno, ali ... od viska glava ne boli  )
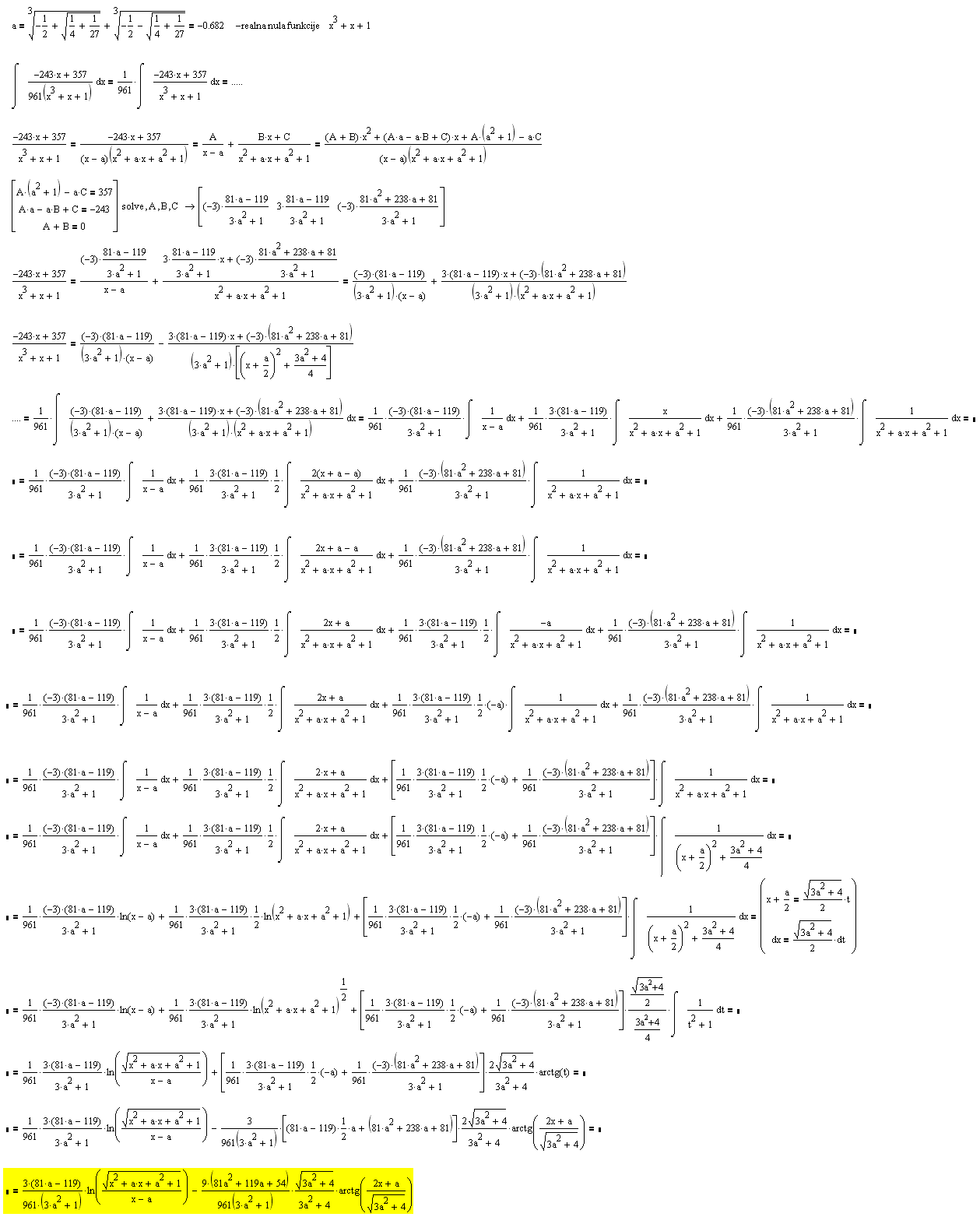
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|