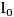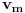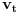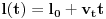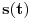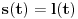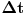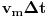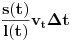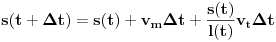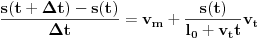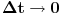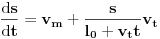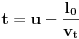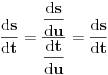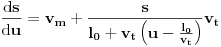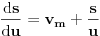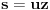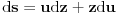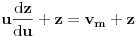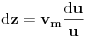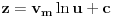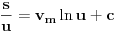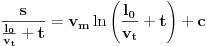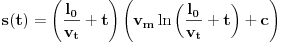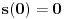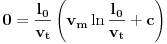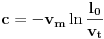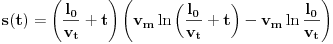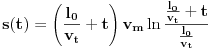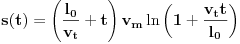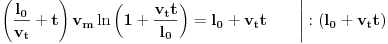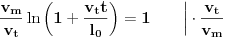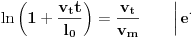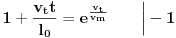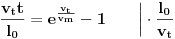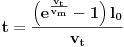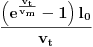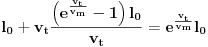mali update

sajt je redizajniran , i ima dosta novih sadrzaja ,

pogotovu iz oblasti vise matematike

od sada ce na sajtu biti stalno postavljani novi sadrzaji

recimo za par dana ce biti postavljen deo o neprekidnosti funkcija ...

www.matematiranje.com

pozdrav,
Aca

Iz dela logički problemi:

U rešenju stoji:

Meni je mnogo zanimljivije pitanje šta bi bilo ako se nešto — recimo, mrav — kreće po nečemu što raste ili se rasteže podjednako — recimo, po gumenoj traci (dakle, zamislimo da je traka jednim krajem pričvršćena, a neko vuče drugi kraj). U tom slučaju problem postaje mnogo teži. U nastavku dajem rešenje, i trudio sam se da ga ispišem tako da ga razumeju i oni koji se ne sreću često s nečim sličnim. Ko bi hteo da prvo pokuša sam, neka ne čita dalje.

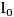
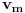
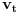
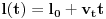
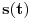
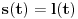
Neka je početna dužina gumene trake, brzina mrava, a brzina rastezanja. Posle vremena dužina trake iznosi . Da bismo rešili problem, potrebno je izračunati pređeni put mrava posle vremena , , i naći koje zadovoljava (u tom momentu mrav stiže do kraja trake). Glavni deo zadatka je, kako se ispostavlja, naći formulu za .

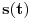
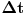
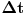
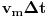
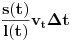
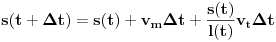
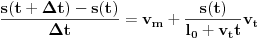
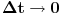
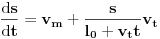
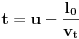
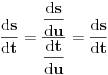
Pretpostavimo, za momenat, da se traka umesto sve vreme, istegne kad god protekne kratak interval . Tada za vreme mrav prelazi put , zahvaljujući sopstvenoj brzini, i još , koliko ga traka pomeri, pa možemo sve zajedno zapisati kao , tj. . Konačno, uzimajući (kako bismo ispoštovali uslov da se traka isteže neprekidno, a ne na kratke intervale), dobijamo . Uvedimo sada smenu . 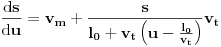Tada je , pa imamo , tj. . 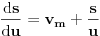Uvedimo još jednu smenu, . 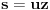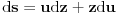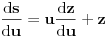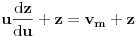Sada važi , pa je , i jednačina glasi , tj. 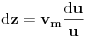, odakle sledi . 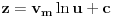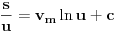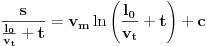Vraćanjem smena najpre imamo , a onda , tj. . 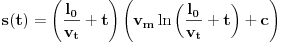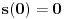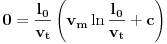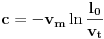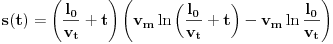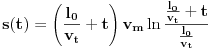Uslov je još i , pa iz dobijamo , te je najzad , što sređujemo kao , i konačno .

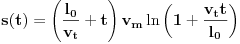
Sada možemo rešiti jednačinu s početka:







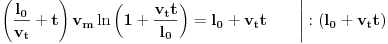
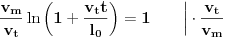
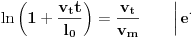
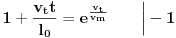
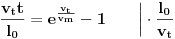
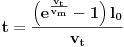
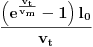
Dakle, u momentu mrav stiže do kraja trake. Dužina trake tada iznosi .

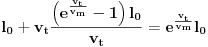
Koristim ovaj sajt ( www.matematiranje.com) za pripremu prijemnog i izbornog iz matematike, medjutim juce sam videla da sajt ne moze da se otvori! Sajt je stvarno dobar za obnavljanje gradiva i potrebni su mi hitno neki zadaci pa se pitam da li su ga mozda izbrisali ili tako nesto... Mada bi pisalo da su promenili adresu... Help!!!!

Da, evo i danas ne može da se otvori...da nisu ovi iz ministarstva umešali prste?

Pa ne znam bas, onda bi trebali i druge sajtove da izbrisu... Onaj sajt je bio najbolji, bas mi treba za prijemni, nadam se da ce da ga vrate uskoro...

A za koji fakultet spremas prijemni?

Arhitektonski...

Hahahaha!

Dobar vic.

_{[Ovu poruku je menjao Cabo dana 08.06.2009. u 21:51 GMT+1]}

I meni je zao sto ne radi, nadam se da je privremeno.

Nista onda.

sajt je ponovo online