ako si nesto radio pa ne znas napisi to(pa cemo ti pomoci), ako nisi nemoj nista, a ako si uradio onda super.

Pozdrav!

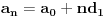
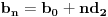
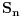
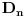
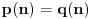
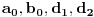
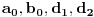
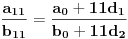
Pretpostavi da je i izracunaj i , ubaci ih u datu jednacinu i dobices jednacinu oblika , gde su i polinomi stepena 2. Posto jednakost mora da vazi za svako izjednaci koeficijente na levoj i desnoj strani i dobices tri linearne jednacije po cetiri nepoznate . Resi sistem linearnih jednacina i dobices izrazene preko jednog slobodnog parametra. Na kraju izracunaj koliko je i trebalo bi da ti se parametar pokrati i da dobijes cistu konstantu. Naravno, sve to vazi pod uslovom da je vrednost parametra takva da je .

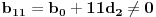
evo mog resenja ako nekoga interesuje, cini mi se da je malo jednostavnije od Nedeljkovog u slucaju da je i tacno.




_{[Ovu poruku je menjao Nemanjich dana 28.06.2008. u 15:41 GMT+1]}

A zasto ti oba niza imaji istu razliku (diferenciju) d?
Ne u 11 clanovima, vec u sumama?

Nisu isti nizovi.
Ne sme im nista biti isto.

Ne valja resenje.

Rezultat je tačan - to što je pisao "d" i "d" umesto "d1" i "d2" nije uticalo na rezonovanje. (Posredi je grafička omaška.)

sutra mi je prijemni na etf-u pa sam bio(a i dalje sam)uzrujan pri resavanju zadatka i napravio nebitnu omasku, valjda necu sutra napraviti gresku slicne tezine pri zaokruzivanju slova za odgovore.

evo bolje verzije