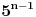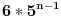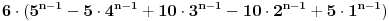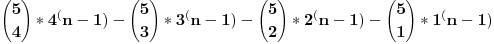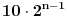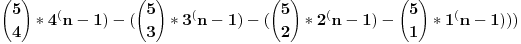[ cmar @ 25.06.2008. 21:53 ] @
|
[ miki069 @ 26.06.2008. 11:15 ] @
U broju 5^(n-1) su ti ukljucene i neke varijacije koje ne dovode do kraja eksperimenta:
1-1-1-1-1-1-1-1-1-1-1 2-2-2-2-2-2-2-2-2-2-2 1-3-4-1-1-2-2-2-2-2-2 ...i mnogo takvih. Kraj eksperimenta je kad se izvuce: 1-2-3-4-5-6 u bilo kom redosledu. od svih varijacija 6^n treba da uzmes one koje se zavrsavaju upravo tako. to su one koje ne prvih (n-6) mesta imaju bilo sta (ali ne i permutaciju od 1-2-3-4-5-6), a na zadnjih 6 mesta bilo koju permutaciju od 1-2-3-4-5-6 broj trazenih je [6^(n-6) - 6!*(n-5)]* 6! [Ovu poruku je menjao miki069 dana 26.06.2008. u 12:32 GMT+1] [ cmar @ 26.06.2008. 20:48 ] @
Cekaj bre bale :) nisi izgleda razumeo sta se trazi. Eksperiment se zavrsava kad u nizu brojeva (koji smo dobili bacanjem) budu svih 6 cifara. Tu sestu cifru dobijamo iz n-tog pokusaja. Ne mora da se baca permutacija sa ciframa od 1 do 6 na kraju da bi se experiment zavrsio. Dobitni niz moze da izgleda i ovako npr.
665553226224431 [ miki069 @ 26.06.2008. 22:47 ] @
To je mnogo lakse onda.
Nisam te razumeo da se permutacija skupa 1-2-3-4-5-6 moze pojaviti razbacano duz resenja. Pa onda je dobro ono tvoje resenje: 5^(n-1)*6. Mozda je profa mislio na postavku kao ja? Ili na neku trecu? Ili je prso na 40 stepeni? Tvoje je resenje OK. Kako da ubedis profu? Neka dodje na forum da nesta nauci ili uzmi kockicu i bacaj, bacaj, bacaj...Neka se uveri. Pozdrav. [ h4su @ 26.06.2008. 23:45 ] @
Ni meni to nije najjasnije sta se trazi al eto.Koliko sam ja skonto trazi se da se odrede n-torke gdje se u n-torci mora pojaviti bar jednom 1,2,3,4,5 i 6, n-fiksan broj.Ako sam te dobro shvatio ond ti rjesenje nije tacno jer za 6*5n-1 imas npr i 222222222222223 npr. a to nije ono sto se trazi.
Mislim da bi trebalo nesto ko sto je miki radio 6!*6^(n-6)-6*5^n a moze biti i da se debelo varam ko zna [Ovu poruku je menjao h4su dana 27.06.2008. u 00:57 GMT+1] [ cmar @ 27.06.2008. 00:11 ] @
kako mislis fiksan broj?
n-to bacanje je ono bacanje posle koga u nizu imas sve sest cifre bar po jednom da se javljaju. mozda te strefi sa 6 bacanja da dobijes sve 6 cifre. A mozda se dan i oduzi... :) [ h4su @ 27.06.2008. 08:16 ] @
Onda imas ono gore samo sto imas ispred sumu n ide od 6 pa dalje.
[ miki069 @ 27.06.2008. 10:32 ] @
Varijacija 222222222222223 je jedna medju svih 6^n varijacija.
n>=6. Od nih svih 6^n varijacija samo 6*5^(n-1) ima trazeno svojstvo da ima pojavu svih 6 brojeva. 6^n je solidno veci broj od 6*5^(n-1). Recimo za n=10: Broj svih varijacija je 6^10 to jest 60 466 176 komada. Od toga samo 6*5^9 to jest 11 718 750 komada ima u sebi pojavu svih 6 cifara. Preostalih 48 i nesta milona varijacija ne ispunjava uslove zadatka - nema pojavu svih 6 cifara. Recimo za n=6: Broj svih varijacija je 6^6 to jest 46 656 komada. Od toga samo 6*5^5 to jest 18 750 komada ima u sebi pojavu svih 6 cifara. Preostalih 27 906 varijacija ne ispunjava uslove zadatka - nema pojavu svih 6 cifara. Ko ne veruje nek napise programce (u VB, Delphiju...) koje generise sve varijacije od 6 elemenata duzine n i broji one koje zadovoljavaju uslov zadatka. Ko ne veruje i ne zna da napise programce, nek se javi okacicu programce sa sve izvornim kodom. Ko ne veruje, ne zna da napise programce i ne razume moje programce... ne znam kako da mu pomognem. Kao sto rekoh, dobro je resenje 6*[5^(n-1)] [ h4su @ 27.06.2008. 10:59 ] @
Opet me nisi ubijedio u to za n=10 ako posmatras 5 cifara na 9 mjesta imamo 5^9 varijacija (znaci moze bit i 111111111 npr),preostalo mjesto se moze popuniti sa 6 cifara pa je to 6*5^9.Međutim tu imamo i 10-torku 1111111112 koja nije ono sto se trazi.
Citat: miki069: Varijacija 222222222222223 je jedna medju svih 6^n varijacija. Ko ne veruje nek napise programce (u VB, Delphiju...) koje generise sve varijacije od 6 elemenata duzine n i broji one koje zadovoljavaju uslov zadatka. Ko ne veruje i ne zna da napise programce, nek se javi okacicu programce sa sve izvornim kodom. Ko ne veruje, ne zna da napise programce i ne razume moje programce... ne znam kako da mu pomognem. Kao sto rekoh, dobro je resenje 6*[5^(n-1)] P.S:Skromnost ti nije bas jaca strana [ cmar @ 27.06.2008. 15:57 ] @
Citat: h4su: Opet me nisi ubijedio u to za n=10 ako posmatras 5 cifara na 9 mjesta imamo 5^9 varijacija (znaci moze bit i 111111111 npr),preostalo mjesto se moze popuniti sa 6 cifara pa je to 6*5^9.Međutim tu imamo i 10-torku 1111111112 koja nije ono sto se trazi. Ne moze n da ti bude 10 a da iz desetog bacanja nemas svih 6 cifara u dobijenom nizu. Ti ne prestajes da bacas dok ne dobijes 6-tu cifru. n je zadnje bacanje (posle kog imas svih 6 cifara!!!!!) I sta sad? Jel tacno ono moje 6*5^(n-1) ? [ zzzz @ 27.06.2008. 19:48 ] @
Citat: Nije! Pogledaj pažljivo šta primjećuje i na šta ukazuje h4su. Da još malo usmjerim. Tvrdim da je moguć uspješan eksperiment sa samo 6 bacanja.Broj različitih načina da ovo ispadne je 720.(123456,123465,.............,654321). Provjeri svoju formulu (6*5^5=18750) Sad ostaje da se vidi kako izračunati broj varijacija koje treba odbiti, jer ne ispunjavaju uslove zadatka.Ajmo. [ cmar @ 28.06.2008. 11:03 ] @
brate, ovo deluje shashavo ali radi :)
nemam pojma na koj si fazon ovo dobio.... [ srki @ 28.06.2008. 12:41 ] @
Pusticu prvo da jos neko pokusa ako zeli, pa ako niko ne dodje do resenja onda cu napisati krajnje jednostavan postupak.
[Ovu poruku je menjao srki dana 28.06.2008. u 14:21 GMT+1] [ h4su @ 28.06.2008. 14:32 ] @
Da pokusam jos jednom.Koliko vidim moje rjesenje i srkijevo se neslazu pa ako moze ko da me ispravi jer ja nevidim u cemu grijesim ako grijesim.
Neka je nakon n bacanja pao posljednji trazeni broj.Imamo ovakvu situaciju npr.: _ _ _ _ 1_ _ _ 3 _ _ _ 2 _ _ _ 4 _ _ _ 6 _ _ _ _ _ _ 5. Znaci na mjestima gdje su crtice moze pasti 5 brojeva ali ne i 5 u ovom slucaju pa imamo 5n-6 varijacija.1,3,2,4,6 mozemo permutirati na 5! nacina tako da imamo 5!*5n-6.Kako 5 brojeva od 6 mozemo izbabrati na 6 nacina imamo konacno rjesenje: 6*5!*5n-6=6!*5n-6. [ cmar @ 28.06.2008. 15:36 ] @
cekaj
ti si kod _ _ _ _ 1_ _ _ 3 _ _ _ 2 _ _ _ 4 _ _ _ 6 _ _ _ _ _ _ 5 racunao variacije crtica (koje su cifre bez petice u ovom slucaju) i permutacije od 1,3,2,4,6 na onim mestima de su 1,3,2,4,6. A resenje moze da bude ne samo _ _ _ _ 1_ _ _ 3 _ _ _ 2 _ _ _ 4 _ _ _ 6_ _ _ _ _ _ 5 nego i: _ _ _ 1_ 3_ _ _ _ _ _ 2 _ 4_ _ _ _ _ _ _ _ _ _ 6_ 5 , ili _ _ _ _ _1 _ _ _ 3_ _ 2 _ _ _ 4 _ _ _ 6 _ _ _ _ _ _ 5 , ili _ _ _ _ 1_ _ _ 3 _ _ _ 2 _ _ _ _ _ _4 _ _ _6 _ _ _ 5. Gde 1,3,2,4,6 setaju medju crtice. A to su sasvim druge moguce varijacije. A? Sta li sam sad reko.... ( srki pomagaj :) ) [ zzzz @ 28.06.2008. 15:58 ] @
h4su predlaže 6!*5^(n-6)
Nije dobro! Fiksirao si ona mjesta za 5 cifara (1,3,2,4,6), akasnije samo permutirao(5!). Ne dozvoljavaš da tu ima i neko ponavljanje , a stvar popravlja neka druga lokacija. Bar sam ja tako shvatio. Ako provjerimo za n=7 na ovaj način:Uzmemo jednu od onih 720 varijacija za n=6 i dodamo jedno prazno mjesto na neku od 6 lokacija.(Ne na kraju.)U svaku od lokacija možemo dodati neki od pet brojeva.To je 6*5=30, ali imamo u svakoj par istih brojeva (ispred-iza), i njihova zamjena ne mijenja ništa.30/2= 15.Dakle imamo 720*15 varijacija.A 6!*5=720*5. Ja se slažem sa Srkijem, i kod mene je tako.Sačekajmo da još neko proba pa ćemo i provjeriti statistički. Zamolićemo i miki069-ja da napravi "programce" koje će raditi na sledeći način. -Generiši slučajni broj 1 do 6. -Kontroliši jesu li svih 6 generisani, a ako nisu ponovi. -(Ugradi brojilo bacanja kocke "n"). -Ako su generisani svih šest zapiši "n" -Poništi brojilo i ponovi sve. -I tako 1000 puta, a tada napiši frekvenciju "n"-ova. Da vidimo kod kojeg "n" se najčešće eksperiment završava pa da uporedimo sa ovim računom. [Ovu poruku je menjao zzzz dana 28.06.2008. u 17:22 GMT+1] [ miki069 @ 28.06.2008. 20:35 ] @
Citat "Od toga samo 6*5^5 to jest 18 750 komada ima u sebi pojavu svih 6 cifara".
Greska - moja. Treba da stoji "od toga treba najmanje 18 750 komada da bi se 100% zavrsio experiment". Ako kontam zadatak (tek sad zahvaljujuci Cmarovim "razjasnjenima") on glasi: "Ako je kocka bacena (n>=6) puta, koliko varijacija (od ukupno 6^n) bi dovelo do okoncanja experimenta?" A nikako: "Koliko ih treba da bi experiment bio 100% uspesan?" - u sta je "Cmar" ubedio i sebe i mene. citiram: "kako mislis fiksan broj? n-to bacanje je ono bacanje posle koga u nizu imas sve sest cifre bar po jednom da se javljaju. mozda te strefi sa 6 bacanja da dobijes sve 6 cifre. A mozda se dan i oduzi..." Dakle n je fiksan broj a ne "kako mislis fiksan broj?" Kecmane, jasan mi je tvoj opisani algoritam 100% i nije mi nikakav za "programce". I OK je to sto trazis - radi provere rezultata. Al ajmo malo pre toga matematicki Mislim ja, jer sam bio zalutao 100%. Ako prsnem "matematicki" - pisem program odmah. Pozdrav tebi i celoj Republici Srpskoj. [Ovu poruku je menjao miki069 dana 28.06.2008. u 23:18 GMT+1] [ zzzz @ 29.06.2008. 01:59 ] @
Citat: miki069:.... Al ajmo malo pre toga matematicki Mislim ja, jer sam bio zalutao 100%. Ako prsnem "matematicki" - pisem program odmah..... I ja sam za to.Ali evo šta ja očekojem od programče iz 1000 (tisuću) pokusa : 15,39,60,75,82,84,81,76,69,61,54,47,40,34,29,26,21,17,.... !!! Objašnjenje:Od 1000 puta dogodiće se da eksperiment uspije 15 x u 6 bacanja.A 39 x u 7 bacanja.Itd, ali otom potom. [ h4su @ 29.06.2008. 11:53 ] @
[ cmar @ 29.06.2008. 12:50 ] @
miki069 ,sta fali mojim , kako ti kazes-"razjasnjenima" ? nemoj molim te..
za kraj experimenta u nizu imamo sigurno po jednu od svake cifre od 1 do 6. To je 6!(faktorijel). i ostale cifre su one razlicite od poslednje izvucene (koju smo cekali). To je 5^(n-6). I to kad se pomnozi imamo: 6!*5^(n-6). De greshim? Otkucao sam i program u paskalu koj simulira 1000 experimenata i kaze da se experiment u proseku zavrsava posle 16-17 bacanja. UVEK! Code: program kocka; type niz=array[1..1000] of integer; var a,c,b:niz; ul, iz:text;i,t,w,u,r, z,n,zbir,l,g,s,srvr:longint; begin z:=0; n:=0; zbir:=0; u:=0; assign(iz,'zad1.out'); rewrite(iz); randomize; for g:=1 to 1000 do begin n:=0; s:=0; while s<>21 do begin i:=random(7); if i>0 then begin a[i]:=i;s:=0; for z:=1 to 6 do s:=s+a[z] ; end; n:=n+1; end; zbir:=zbir+n; for l:=1 to 6 do a[l]:=0; end; srvr:=zbir div 1000; writeln(iz,srvr);writeln(iz,zbir); close(iz); end. Jel to po verovatnoci? il ovaj moj program ne ume lepo da baca kockicu... :) [ h4su @ 29.06.2008. 14:16 ] @
[ srki @ 30.06.2008. 03:32 ] @
Je l' mozes da nam objasnis kako si dosao do ove formule? Dobijes na kraju isto sto sam i ja dobio ali mi nije jasno na koji nacin si ti dosao do ovoga sto si gore napisao.
[ miki069 @ 30.06.2008. 06:37 ] @
Ne baca lepo kocku.
While s<>21. Pa i varijacija 2-2-2-5-5-5 ispunjava uslov S=21. Kao i varijacija 1-2-2-4-6-6 Kao i varijacija 1-1-3-4-6-6 Nigde ne proveravas da su sve cifre razlicite. [ h4su @ 30.06.2008. 08:36 ] @
Citat: srki: Je l' mozes da nam objasnis kako si dosao do ove formule? Dobijes na kraju isto sto sam i ja dobio ali mi nije jasno na koji nacin si ti dosao do ovoga sto si gore napisao. Evo kako sam dosao do toga:Neka je u n-tom bacanju pala zadnja trazena cifra.Ako posmatramo jednu petorku brojeva na n-1 mjesta imamo 5n-1 varijacija.Da bi n-to bacanje bilo zadnje treba izbaciti sve varijacije koje su sastavljene od 4 cifre koje mozemo izabrati od ovih 5 na 5 nacina pa imamo 5*4n-1 varijacija.S obzirom da u 5*4n-1 imamo uracunte i sve varijacije sa 3 razlicita elementa i to ocigledno racunajuci ih vise puta(Npr za cetvorku (1,2,3,4 ) i cetvorku (1,2,3,5) imamo iste trojke (1,2,3) koje onda racunam visestruk0) treba oduzeti sve varijacije od 3 elementa od ovih varijacije od 4 elementa itd. I na kraju posto mozemo izabrati 5 na 6 nacina to sve jos pomnozimo sa 6. Kako si ti dosao do trazenog rjesenja ? [ miki069 @ 30.06.2008. 10:36 ] @
Napravio sam "programce" koje generise varijacije duzine n od datih k elemenata i prebrojava u kojima se pojavljuje svih k elemenata. (n>=k).
Za k=6 situacija je sledeca: za n=6 ima ukupno 46 656 varijacija od kojih 720 zadovoljava uslove zadatka. za n=7 ima ukupno 279 936 varijacija od kojih 15 120 zadovoljava uslove zadatka. za n=8 ima ukupno 1 676 616 varijacija od kojih 191 520 zadovoljava uslove zadatka. za n=9 ima ukupno 10 077 696 varijacija od kojih 1 905 120 zadovoljava uslove zadatka. za n=10 ima ukupno 60 046 176 varijacija od kojih 16 435 440 zadovoljava uslove zadatka. za n=11 ima ukupno 362 797 056 varijacija od kojih 129 230 640 zadovoljava uslove zadatka. "programce" sljaka 100% ispravno jer pisem varijacije u txt fajl i markiram one koje zadovoljavaju. mogu da okacim primere txt fajlova. Ajd nek sad neko ubaci ove n-ove u Srkijevu formulu i mislim da ce biti OK - isti rezultat. Ja necu jer nisam resio matematicki. [ zzzz @ 30.06.2008. 12:02 ] @
Citat: miki069: Napravio sam "programce" koje generise varijacije duzine n od datih k elemenata i prebrojava u kojima se pojavljuje svih k elemenata. (n>=k). Nije ovo dovoljno.Trebaš odbaciti sve one kojima poslednja brojka nije jedina unutar te varijacije. Po formuli za n=7 umjesto 15120 imamo 10800,itd. --------------------- I ja sam radio kao h4su.(Odbijao varijacije koje ne ispunjavaju uslove i sprečavajući višestruka odbijanja pojave se one zagrade.I kad ih se riješim izađe kao kod srkija. Ja nemam ideju za neki jednostavniji postupak.Izgleda da srki ima? [ srki @ 30.06.2008. 12:04 ] @
Miki, ti si izgleda nesto mnogo siguran :) ali opet si negde pogresio. Za n=7 rezultat je 10800 sto je dobio i Milan na prethodnoj strani bez koriscenja one formule. Ajde ostavi taj fajl sa 7 cifara, moguce je da ti se neke varijacije ponavljaju.
Citat: h4su: Da bi n-to bacanje bilo zadnje treba izbaciti sve varijacije koje su sastavljene od 4 cifre koje mozemo izabrati od ovih 5 na 5 nacina pa imamo 5*4n-1 varijacija.S obzirom da u 5*4n-1 imamo uracunte i sve varijacije sa 3 razlicita elementa i to ocigledno racunajuci ih vise puta(Npr za cetvorku (1,2,3,4 ) i cetvorku (1,2,3,5) imamo iste trojke (1,2,3) koje onda racunam visestruk0) treba oduzeti sve varijacije od 3 elementa od ovih varijacije od 4 elementa itd. 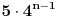 sadrzi i varijacije od 2 i jednog elementa koje se ponavljaju vise puta a te varijacije koje imaju 3 elementa sadrzi i varijacije od 2 i jednog elementa koje se ponavljaju vise puta a te varijacije koje imaju 3 elementa 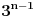 isto tako nekoliko puta ponavljaju varijacije koje imaju 2 elementa i 1 element. Zato mi i dalje nije jasno kako si iz cuga mogao da napises onu formulu znajuci gde treba da oduzmes a gde da saberes. isto tako nekoliko puta ponavljaju varijacije koje imaju 2 elementa i 1 element. Zato mi i dalje nije jasno kako si iz cuga mogao da napises onu formulu znajuci gde treba da oduzmes a gde da saberes. Ja sam resio na sledeci nacin. Neka 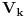 predstavlja broj varijacija gde u predstavlja broj varijacija gde u  mesta mozemo da rasporedimo (sa ponavljanjem) tacno mesta mozemo da rasporedimo (sa ponavljanjem) tacno  elemenata tako da svaki element bude prisutan barem jedanput. elemenata tako da svaki element bude prisutan barem jedanput. Poslednje mesto mozemo da izaberemo na 6 nacina i to se pomnozi sa 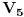 - broj nacina na koji mozemo postaviti ostale brojeve u - broj nacina na koji mozemo postaviti ostale brojeve u  tako da svih 5 brojeva bude prisutno. Trazeni rezultat je gde je tako da svih 5 brojeva bude prisutno. Trazeni rezultat je gde je 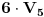 . .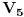 je jednak broju svih varijacija sa ponavljanjem od tih 5 elemenata minus broj varijacija gde se pojavljuje tacno 4, 3, 2 i 1 element: je jednak broju svih varijacija sa ponavljanjem od tih 5 elemenata minus broj varijacija gde se pojavljuje tacno 4, 3, 2 i 1 element: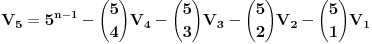 Dalje: 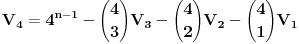 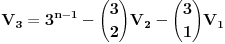 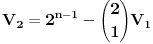 i 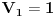 Kada sve to zamenimo onda dobijemo trazeni rezultat. Jednostavnije nisam pokusao niti razumem kako ste vi resili jednostavno bez ovih zamena. [Ovu poruku je menjao srki dana 01.07.2008. u 06:47 GMT+1] [ h4su @ 30.06.2008. 12:36 ] @
Citat: srki: Ali isto tako i 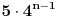 sadrzi i varijacije od 2 i jednog elementa koje se ponavljaju vise puta a te varijacije koje imaju 3 elementa sadrzi i varijacije od 2 i jednog elementa koje se ponavljaju vise puta a te varijacije koje imaju 3 elementa 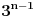 isto tako nekoliko puta ponavljaju varijacije koje imaju 2 elementa i 1 element. Zato mi i dalje nije jasno kako si iz cuga mogao da napises onu formulu znajuci gde treba da oduzmes a gde da saberes. isto tako nekoliko puta ponavljaju varijacije koje imaju 2 elementa i 1 element. Zato mi i dalje nije jasno kako si iz cuga mogao da napises onu formulu znajuci gde treba da oduzmes a gde da saberes. Pa daleko je to bilo od "iz cuga".Mislim da sam dovoljno objasnio. [ miki069 @ 30.06.2008. 13:12 ] @
Evo kacim txt za duzinu n=7.
Pored varijacije koja zadovoljava trazene uslove levo njen redni broj (od 1 do 279 936) a desno OK i njen brojac. Zbog ogranicenja fajla na 1024K dao sam samo one varijacije koje su OK. Ima ih tacno 15 120. Ni manje ni vise. Nesta ste mi vi previse "sigurni". U tim formulama previse oduzimate. Aj stavite bar negde +. Mozda bude tacno. Ovo je 100% sigurno. Brute-force [Ovu poruku je menjao miki069 dana 30.06.2008. u 14:43 GMT+1] [ zzzz @ 30.06.2008. 15:09 ] @
Citat: miki069: Nesta ste mi vi previse "sigurni". U tim formulama previse oduzimate. Aj stavite bar negde +. Mozda bude tacno. Ovo je 100% sigurno. Brute-force Grubo ti je ovo "programce". pogledaj naprimjer ovo: 11191 ------> 1 2 3 4 5 6 1 OK 200 Ovakvo bacanje se neće desiti nikad, jer poslije šest bacanja eksperiment se prekida jer imaš svih šest brojeva. srki je odlično uradio, a i objasnio postupak.Nema nikakve sumnje u ispravnost rješenja.Nije ovo baš lagan zadatak, ali je lakši nego što sam ja mislio. (Rješavao sam ga više od 2 sata i bio pomalo nesiguran, ali sada više nisam.) [ miki069 @ 30.06.2008. 15:33 ] @
Programce generise varijacije od k elemenata duzine n.
Iako se vrti u vecini kladionica u Srbiji vec 10 godina - ne resava ovaj zadatak. Znaci kad kazemo n=7 kocka se ne baca obavezno 7 puta? Vec do pojave 1-2-3-4-5-6? Ako je n=10 ne mora se bacati 10 puta??? Moze i samo 6 puta. Opet nisam skontao zadatak. Ja sam uradio kako sam i napisao. Ako je n=7, da se baca obavezno 7 puta, sto ne valja. Stize drugo programce expresno. Dace valjda isti rezultat kao i Srkijeva formula. [Ovu poruku je menjao miki069 dana 30.06.2008. u 16:44 GMT+1] [Ovu poruku je menjao miki069 dana 30.06.2008. u 16:46 GMT+1] [ miki069 @ 30.06.2008. 16:57 ] @
Posle ispravne Kecmanove sugestije "izbaci sve varijacije u kojma se zadnji broj vec pojavljivao" evo ga rezultati novog brute-force programcica:
za n=6 ima ukupno 46 656 varijacija od kojih 720 zadovoljava uslove zadatka. za n=7 ima ukupno 279 936 varijacija od kojih 10 800 zadovoljava uslove zadatka. za n=8 ima ukupno 1 676 616 varijacija od kojih 100 800 zadovoljava uslove zadatka. za n=9 ima ukupno 10 077 696 varijacija od kojih 756 000 zadovoljava uslove zadatka. za n=10 ima ukupno 60 046 176 varijacija od kojih 5 004 720 zadovoljava uslove zadatka. Ovo bi trebalo da zadovoljava rezultate Srkijeve formule. Nek neko proveri. Da ne bude da sam samo izracunao, kacim txt za n=7. I zipovano za n=8. [Ovu poruku je menjao miki069 dana 30.06.2008. u 18:26 GMT+1] [ zzzz @ 30.06.2008. 19:17 ] @
Hvala na trudu.Rezultati se slažu računajući po formuli i ovo tvoje brojanje
grubom silom.Ja sam već dao nešto ovako: 15,39,60,75,82,84,81,... a ovo su omjeri broja varijacija koje zadovoljavaju i ukupnog broja varijacija *1000.I to za slučaj da eksperiment uspije u 6,7,8,9,10,..itd....bacanja. [ miki069 @ 30.06.2008. 21:24 ] @
za n=11 ukupan broj varijacija je 362 797 056 a od toga 30 618 000 zadovoljavaju uslove zadatka.
Hvala tebi Kecmane na smernicama za program. Svaka cast Srkiju na formuli, h4su i tebi na izracunavanjima. Pozdrav. [ srki @ 30.06.2008. 22:47 ] @
Citat: h4su: Pa daleko je to bilo od "iz cuga".Mislim da sam dovoljno objasnio. zzzz, je l' mozes ti da napises tvoj postupak, slicno kao sto sam ja napisao? [Ovu poruku je menjao srki dana 01.07.2008. u 01:31 GMT+1] [ miki069 @ 01.07.2008. 07:12 ] @
za n=12 ukupan broj varijacija je 2 176 782 336 a od toga 177 645 560 zadovoljavaju uslove zadatka
[ h4su @ 01.07.2008. 07:45 ] @
Citat: srki: Ali isto tako i 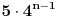 sadrzi i varijacije od 2 i jednog elementa koje se ponavljaju vise puta a te varijacije koje imaju 3 elementa sadrzi i varijacije od 2 i jednog elementa koje se ponavljaju vise puta a te varijacije koje imaju 3 elementa 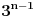 isto tako nekoliko puta ponavljaju varijacije koje imaju 2 elementa i 1 element. Zato mi i dalje nije jasno kako si iz cuga mogao da napises onu formulu znajuci gde treba da oduzmes a gde da saberes. isto tako nekoliko puta ponavljaju varijacije koje imaju 2 elementa i 1 element. Zato mi i dalje nije jasno kako si iz cuga mogao da napises onu formulu znajuci gde treba da oduzmes a gde da saberes. Sam si gore sve rekao.Posmatrajmo 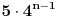 - -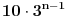 .Kako si gore rekao .Kako si gore rekao 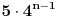 sadrzi varijacije od 2 i jednog elementa koje isto tako sadrzi i sadrzi varijacije od 2 i jednog elementa koje isto tako sadrzi i 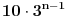 (tako da ih u ovom trenutku mogu zanemariti) medjutim vidim da kad posmatram samo ovaj izraz (tako da ih u ovom trenutku mogu zanemariti) medjutim vidim da kad posmatram samo ovaj izraz 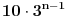 vidim da imam visestruko racunanje nekih varijacija pa ih trebam oduzeti od ove itd. vidim da imam visestruko racunanje nekih varijacija pa ih trebam oduzeti od ove itd.Cestitam tebi na datom rjesenju ne ostavlja nikakvu sumnju u ispravnost rjesenja i pozz za kecmana i mikija. [ zzzz @ 01.07.2008. 12:32 ] @
Citat: Ma kakva metoda.To je bilo obično "odreži pa probaj",ali je funkcionisalo. -Odmah sam pomislio da je zadatak jednostavan.Treba samo od 6*5^(n-1) odbiti sve varijacije koje nemaju svih pet brojeva u sebi,i da je dovoljno izračunati 4^(n-1) jer se tu sadrže i one sa 3,2 i 1 brojem,a zatim pošto četvorke možemo oformiti na 5 načina imamo ovakvu formulu: 6*(5^(n-1)-5*4^(n-1))...i gotovo! -Onda sam lako izračunao varijacije za n=6 i n=7 (6!=720 i 15*6!=1080).Za veće n nije baš lako.Isprobam svoju formulu i vidim da dobijam neke negativne brojeve!Za n=6 dobijem -11970, a za n=7 -122880.Nešto ne valja.Primjetim da sam imao višestruko ponavljanje varijacija od tri broja zbog korištenja 5 različitih grupa sa 4 broja. Treba te trojke izbiti iz četvorki ali ne sve.ALi i varijacije sa 2 pa i 1 elementom prave problem.Opet idem na spasonosnu probu sa 6*(5^(n-1)-(5*4^(n-1)-10*3^(n-1))) Bliže sam ,ali i znam da nisam smio oduzeti onoliko varijacija sa tri elementa(koji mogu izabrati na 10 načina).Još sam malo probao provjeriti kako se u varijacijama sa dva elementa (kojih takođe ima sa deset različitih parova) ponavljaju varijacije sa jednim elementom.Ovih ima 5 različitih.Sad sam već bio prilično siguran da treba samo nastaviti na isti način pisati formulu. 6*(5^(n-1)-(5*4^(n-1)-(10*3^(n-1)-(10*2^(n-1)-5)))) Lijepo izgleda,a i probe za n=6 i 7 daju prave rezultate.Hm,možda je i dobro.Recimo siguran sam bio 99 %.Ali mislim da na ispitu nebih s ovim prošao, pogotovo zbog utrošenog vremena. [ srki @ 01.07.2008. 13:39 ] @
Citat: zzzz: Lijepo izgleda,a i probe za n=6 i 7 daju prave rezultate.Hm,možda je i dobro.Recimo siguran sam bio 99 %.Ali mislim da na ispitu nebih s ovim prošao, pogotovo zbog utrošenog vremena. Ako zanemarimo vreme prosao bi na ispitu ako bi posle indukcijom dokazao da ta formula vazi i kada je n>6. Mnogi zadaci se najlakse resavaju na taj nacin, isprobavanjem nadjes formulu i onda indukcijom dokazes da ona vazi u opstem slucaju. [ zzzz @ 01.07.2008. 13:51 ] @
miki069 pobogu, ustavi to programce izgoriće procesor.
Rješenje je sigurno dobro.Ovo što je napisao srki svako može shvatiti da vrijedi: A to je da varijacije sa ponavljanjem mogu sadržavati: sve elemente,ima ih bez jednog elementa,bez dva itd i na kraju samo sa jednim elementom.(Kao sportska prognoza sa sve samim fiks 1).Suma svih mogućih varijacija jednaka je zbiru ovih gore navedenih. Ko bi se tome nadao.Rasparčamo nešto u dijelove i onda tvrdimo da je suma tih djelova jednaka onom od čega su nastali.Ako je ovo istina onda je i formula u redu. [ cmar @ 01.07.2008. 15:46 ] @
Citat: miki069: Ne baca lepo kocku. While s<>21. Pa i varijacija 2-2-2-5-5-5 ispunjava uslov S=21. Kao i varijacija 1-2-2-4-6-6 Kao i varijacija 1-1-3-4-6-6 Nigde ne proveravas da su sve cifre razlicite. ma sta mi rece... Code: ...begin n:=0; s:=0; while s<>21 do begin i:=random(7); if i>0 then begin a[i]:=i;s:=0; for z:=1 to 6 do s:=s+a[z] ; end; n:=n+1; end; zbir:=zbir+n; for l:=1 to 6 do a[l]:=0; end;... pogledaj malo bolje ovaj red 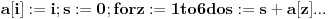 . .Generisano  se stavlja na i-to mesto u nizu a. Znaci npr. trojka na trece ,petica na peto ...Svaka sledeca trojka ili petica idu ponovo na ta dva mesta (menjaju prethodnu trojku ili peticu). Jednostavno prve 6 cifre u nizu se stavlja na i-to mesto u nizu a. Znaci npr. trojka na trece ,petica na peto ...Svaka sledeca trojka ili petica idu ponovo na ta dva mesta (menjaju prethodnu trojku ili peticu). Jednostavno prve 6 cifre u nizu  mogu biti samo ,redom 1,2,3,4,5,6. A ne ko sto si ti reko i 2-2-2-5-5-5. Dok sve 6 ne budu prisutne u nizu zbir nece biti 21 a ni experiment nece biti zavrsen. Znaci moj program ipak lepo baca kockicu... mogu biti samo ,redom 1,2,3,4,5,6. A ne ko sto si ti reko i 2-2-2-5-5-5. Dok sve 6 ne budu prisutne u nizu zbir nece biti 21 a ni experiment nece biti zavrsen. Znaci moj program ipak lepo baca kockicu...[Ovu poruku je menjao cmar dana 01.07.2008. u 17:24 GMT+1] [ cmar @ 01.07.2008. 16:20 ] @
Danas polozih kombinatoriku i grafove (Diskretne strukture II) !
Jedva se provukoh. Driblao me profa pola sata. Sreca nije me zezao sa kombinatorikom mnogo. Cela zackoljica u vezi ove teme je teorema iskljucenja i ukljucenja. Samo se ona primeni i eto ga. Evo je ta teorema: [att_img] [ miki069 @ 02.07.2008. 01:45 ] @
Nisam video a(i) = i.
Program lepo baca 6 kockica i lepo broji kad je 1-2-3-4-5-6. [Ovu poruku je menjao miki069 dana 02.07.2008. u 08:47 GMT+1] [ cmar @ 02.07.2008. 11:41 ] @
Program lepo baca JEDNU kockicu!
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|