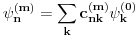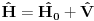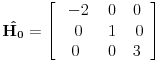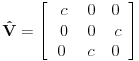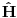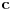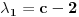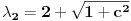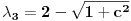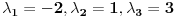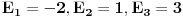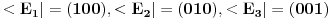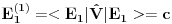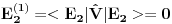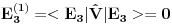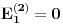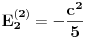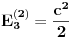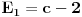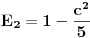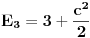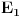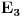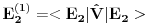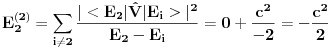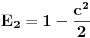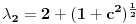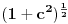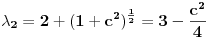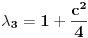[ petarm @ 02.07.2008. 16:50 ] @
|
[ Milan Milosevic @ 03.07.2008. 08:21 ] @
Zato sto cine jedan kompletan skup svojstvenih stanja.
Svaka talasna funkcija moze da se predstavi u takvom skupu. Svojstvene funkcije nepertubovanog hamiltonijana mogu explicitno da se rese i zato predstavljaju pogodni bazis. Jos su i ortonormirane. [ petarm @ 03.07.2008. 10:16 ] @
Da nisam razmisljao! Naravno hvala ti!
[ petarm @ 03.07.2008. 15:09 ] @
[ tomkeus @ 08.07.2008. 20:14 ] @
Reši svojstveni problem
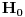 da bi našao energetske nivoe i stanja (svojstvene vrednosti i vektori matrice da bi našao energetske nivoe i stanja (svojstvene vrednosti i vektori matrice 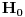 ). Svojstvene vrednosti ove matrice su nedegenerisane tako da imaš tri energijska nivoa ). Svojstvene vrednosti ove matrice su nedegenerisane tako da imaš tri energijska nivoa 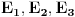 sa pripadajućim stanjima sa pripadajućim stanjima 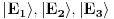 . Prva popravka i-tog nivoa je . Prva popravka i-tog nivoa je 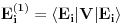 . Druga popravka i-tog nivoa je . Druga popravka i-tog nivoa je 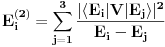 . U ove formule samo ubaci svojstvene vektore koje si izračunao i to je to. . U ove formule samo ubaci svojstvene vektore koje si izračunao i to je to.[ petarm @ 09.07.2008. 11:32 ] @
[ tomkeus @ 09.07.2008. 12:20 ] @
[ petarm @ 09.07.2008. 12:25 ] @
[ tomkeus @ 09.07.2008. 16:43 ] @
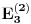 je u redu. Mislim da si kod računanja je u redu. Mislim da si kod računanja 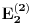 napravio računsku grešku zato što ako rešiš svojstveni problem napravio računsku grešku zato što ako rešiš svojstveni problem 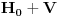 pa onda dobijene svojstvene vrednosti razviješ oko c=0 do drugog stepena moraš da dobiješ isti rezultat kao i primenom perturbacionog metoda drugog reda a pa onda dobijene svojstvene vrednosti razviješ oko c=0 do drugog stepena moraš da dobiješ isti rezultat kao i primenom perturbacionog metoda drugog reda a 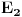 dobijeno razvojem svojstvenih vrednosti i metodom perturbacija se ne slažu za razliku od ostalih. dobijeno razvojem svojstvenih vrednosti i metodom perturbacija se ne slažu za razliku od ostalih.Citat: petarm:I gde ja koristim 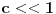 ? ?Koristiš ga da bi uopšte mogao da primeniš metod perturbacija jer je zahvaljujući tom uslovu V mala popravka pa razvoj daje zadovoljavajuće rezultate. [ petarm @ 10.07.2008. 23:57 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|