Afini prostori služe da se geometrijska slika o vektorima kao usmerenim dužima dobro definiše (tj. vektori su definisani kao uređeni parovi tačaka). Vektorski prostori su algebarska kategorija i tiču se samo datog skupa i osobina operacija definisanih na njemu bez obzira kakva je realizacija tog skupa, tj. da li su u pitanju strelice, trouglići, babe, žabe itd.

Jedina sustinska razlika izmedju linearnih i afinih prostora je sto u linearnim postoji tacka koja odgovara nula-vektoru (izabrani koordinatni pocetak) a u afinim prostorima su sve tacke potpuno ravnopravne. Od bilo kog linearnog prostora mozes napraviti afini ako "zaboravis" da tacke (to jest vektore) mozes da sabiras, vec da eventualno mozes da ih oduzimas, kada kao rezultat dobijas vektor. Isto tako, od afinog prostora mozes napraviti linearni izborom koordinatnog pocetka.

U knjizi profesora Musickog ''Matematicke osnove teorijske fizike'' on uvodi pojam prostora kojeg definise kao skup matematickih objekata sa tacno definisanom strukturom. A onda kaze ako je takav prostor snabdeven operacijama sabiranja elemenata prostora i mnozenja istih skalarom onda je to vektorski prostor. Zapravo on pod prostorom smatra afini prostor ili ne kada tako definise?


Ne razumem ovo?


Kako u afinom da izaberem koordinatni pocetak?

Dakle, te objekte (tacke) koje u slucaju vektorskog prostora mozes da sabiras i mnozis skalarom, u slucaju afinog prostora mozes samo da odulzimas, pri cemu je rezultat vektor, pa je 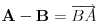Preciznije govoreci, uvodi se pojam vektora kao klase ekvivalencije uredjenih parova tacaka, ali sa njima mozes da racunas kao da su u pitanju "razlike tacaka".

U afinom prostoru (ako zelis da dobijes vektorski) koordinatni pocetak biras potpuno proizvoljno, pa onda tacki pridruzujes vektor .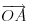

Ako bude nejasnoca, onda prepisi definiciju afinog prostora iz knjige ovde, pa da tumacimo sat ostane nejasno.

Afini -dimenzioni prostor predstavlja skup tacaka definisanih kao pri cemu su koordinate tacke.

Moze li se prihvatiti ovakva def? Cesto se koristi u nekim knjigama iz fizike!

Npr. baza vektorskog prostora je afina kada vektori koji je sačinjavaju nisu međusobno okomiti i različite su dužine.

Evo primene i naišao sam na sl. zadatak:
Za ravan de…finisanu sa x + 2y - 3z =5 odrediti skup rešenja, a…fini potprostor i direktrisu.

U knjizi G.Kalajdžića ima samo jedan primer, ali mi i dalje nije jasno kako odrediti direktrisu?

Kao sopstveni potprostor generisan sopstvenim vektorima, naravno. Imaš primere sličnih zadataka u „zadacima sa ispitnih rokova“ kod Miše. ;-)

Ja bih bio jako srecan kad bi mi ovo bilo tacno?




Gornja transformacija je linearna, a ova ispod nje je afina!