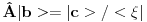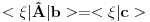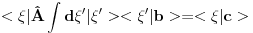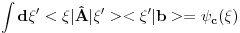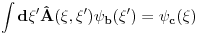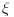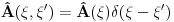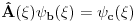[ petarm @ 13.07.2008. 00:44 ] @
|
[ kajla @ 23.07.2008. 12:52 ] @
Pa to mozes da uzmes samo u slucaju kad ti je operator dijagonalan u koordinatnoj reprezentaciji tj. kad je funkcija kordinate. (npr. operator potencijala, naravno ne za mag. polje)
poz. [ kajla @ 23.07.2008. 17:17 ] @
Pa da posto ti Kronekerova delta prelazi u Dirakovu delta f-ju.
pozdrav. [ petarm @ 23.07.2008. 18:36 ] @
Ovo je zanimljivo! Na jednom delu ovog Foruma ja sam postavio pitanje na koje mi je odgovorio tomkeus pa me zanima sta ti mislis o tome. Isto pitanje?
Citat: petarm: I da li je pravilno reci da je delta fja prosirenje Kronekerovog delta simbola na kontinuum? Citat: tomkeusU rigoroznom matematičkom smislu: Nemam pojma, zato što ne znam kako matematičari definišu "proširenje" Kronekereovog simbola na kontinuum, ako uopšte to i rade. U smislu analogija: Može se reći zato što ako integral posmatramo kao "kontinualnu sumu" delta funkcija se ponaša kao Kronekerov simbol zato što "ubija" sumu. Slikovitije: Ovako deluje Kronekerov simbol 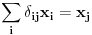 Ovako deluje delta funkcija 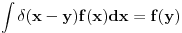 Kao što vidiš, upotreba je totalno analogna. Citat: Mislis u smislu analogona ili strogo matematicki? [ kajla @ 23.07.2008. 21:52 ] @
Pa ako hoces strogo da pokazes onda moras da postupis slicno kao kad sa darbuovih suma prelazis na integral. Mada strogo govereci integral koji sadrzi deltu nije rimanov, rimanovi integral imaju osobinu da ako integrand promenis na skupu mere nula vrednost integrala se ne menja sto u ovom slucaju nije zadovoljeno. Pogledaj malo o Lebegovim integralima ako te to zanima, mada sto se fizike tice insistiranje na rigoroznosti je stranputica. (ako je verovati Landau, mada i moje skromno iskustvo mi govori da je ovo istina)
pozdrav. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|