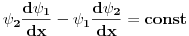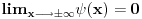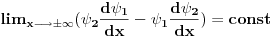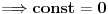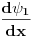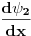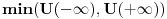[ petarm @ 14.07.2008. 11:52 ] @
|
[ kajla @ 23.07.2008. 12:47 ] @
Za vezano stanje ti je energija cestice manja od min(U(-inf),U(inf)) tako da ti talasna fja eksponencijalno opada u beskonacnosti pa samim tim i njen prvi izvod.
pozdrav. [ petarm @ 23.07.2008. 13:00 ] @
Citat: kajla: Za vezano stanje ti je energija cestice manja od min(U(-inf),U(inf)) tako da ti talasna fja eksponencijalno opada u beskonacnosti pa samim tim i njen prvi izvod. pozdrav. Sta ti je min(U(-inf),U(inf))? [ kajla @ 23.07.2008. 17:20 ] @
inf skacenica od infinity, tj. potencijal u plus i minus beskonacno (pa manji od ta dva).
pozdrav. [ petarm @ 23.07.2008. 18:03 ] @
[ kajla @ 23.07.2008. 21:42 ] @
Pa zato sto u suprotnom slucaju cestica nece vrsiti finitno kretanje tj. verovatnoca da se cestica nadje na velikim udaljenostima nece eksponencijalno opadati (E-U ce tada biti vece od nule tako da ce sinusoida da bude resenje sredingerove jne) a kada je E<U resenje je eksponencijalno opadajuca f-ja. (sve ovo sto sam napisao imam detaljno objasnjeno kod Landau-a, mozes da pogledas i poglavlje vezano za kvaziklasicnu aproksimaciju)
pozdrav. [ petarm @ 24.07.2008. 22:07 ] @
Jel mozes da preciziras gde to sve ima tacno napisano kod Landau-a posto ga sad konacno imam kod sebe! Orijentaciono ako ne mozes tacno! Ja imam ovaj prevod s ruskog (od Dragise Ivanovica) "Kvantna neralativisticka teorija" - Landau, Lifsic
Unapred hvala! [ kajla @ 24.07.2008. 22:29 ] @
Pogledaj 18. i 21. poglavlje (ja imam rusku knjigu tako da se brojevi strana razlikuju) Mozes da pogledas i kvaziklasicnu aproksimaciju (prvih par poglavlja iz tog dela)
pozdrav. [ petarm @ 25.07.2008. 16:03 ] @
Hajde da citiram nesto iz Landau-a.
''Skrecemo paznju na cinjenicu da se u kvantnoj mehanici pri finitnom kretanju cestica moze nalaziti i u onim oblastima prostora u kojima je  . Verovatnoca nalazenja cestice, iako i tezi brzo ka nuli sa povecanjem rastojanja u dubini te oblasti, ipak je razlicita od nule za sva konacna rastojanja'' . Verovatnoca nalazenja cestice, iako i tezi brzo ka nuli sa povecanjem rastojanja u dubini te oblasti, ipak je razlicita od nule za sva konacna rastojanja''''Smatracemo da fja 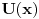 za za 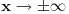 tezi ka konacnim granicama (ali nikako ne mora biti monotona fja). Granicu tezi ka konacnim granicama (ali nikako ne mora biti monotona fja). Granicu 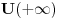 uzecemo za pocetak racunanja energije [tj. stavicemo uzecemo za pocetak racunanja energije [tj. stavicemo 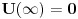 ], a ], a 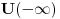 obelezicemo sa obelezicemo sa 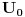 i smatracemo da je i smatracemo da je 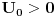 . Diskretni spektar se nalazi u oblasti takvih vrednosti energije za koje cestica ne moze preci u beskonacnost (vrlo daleko). Zbog toga energija mora biti manja od obe granice . Diskretni spektar se nalazi u oblasti takvih vrednosti energije za koje cestica ne moze preci u beskonacnost (vrlo daleko). Zbog toga energija mora biti manja od obe granice 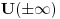 , tj. mora biti negativna , tj. mora biti negativna  '' ''Po meni tvoj zakljucak sledi iz ova dva citata Landau-a. Jesam li u pravu? Naravno ne mora se uzeti ovaj uslov 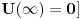 i to ce nas tacno prebaciti u ono sto si ti napisao i to ce nas tacno prebaciti u ono sto si ti napisao 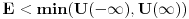 . Jel tacno? . Jel tacno? [ kajla @ 25.07.2008. 16:23 ] @
Da i toga sto u klasicno nedostupnoj oblasti talasna fja mora ekponencijalno da opada.
pozdrav. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|