[ adnanK @ 14.07.2008. 14:06 ] @
| Dakle, ne smije se koristiti stepenovanje, vec samo osnovne racunske operacije, tj, + - x i /. Takodje svaki broj smijete koristiti samo jednom. |
|
[ adnanK @ 14.07.2008. 14:06 ] @
[ Predrag Supurovic @ 14.07.2008. 16:13 ] @
Ako mislis da se koriste smo brojevi 5, 2, 3 i 3 tesko, a ako mogu da se koriste kao cifre onda je (53-3)*2
[ petarm @ 14.07.2008. 20:52 ] @
[ petarm @ 14.07.2008. 22:24 ] @
Citat: adnanK: Dakle, ne smije se koristiti stepenovanje, vec samo osnovne racunske operacije, tj, + - x i /. Takodje svaki broj smijete koristiti samo jednom. Ja cu definisati 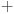 kao kao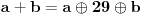 gde je  sabiranje brojeva, a sabiranje brojeva, a 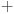 neka osnovna operacija ovako definisana neka osnovna operacija ovako definisana 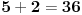 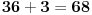 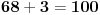 [ Bojan Basic @ 14.07.2008. 22:48 ] @
S ova
 broja i broja i  operacije može se dobiti najviše operacije može se dobiti najviše 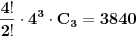 različitih rezultata (prvi činilac predstavlja broj mogućih rasporeda ova četiri broja, pri čemu delimo sa različitih rezultata (prvi činilac predstavlja broj mogućih rasporeda ova četiri broja, pri čemu delimo sa 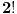 jer se dva puta pojavljuje isti broj; drugi činilac prebraja operacije koje se mogu udenuti između određenog rasporeda datih brojeva; treći činilac je jer se dva puta pojavljuje isti broj; drugi činilac prebraja operacije koje se mogu udenuti između određenog rasporeda datih brojeva; treći činilac je 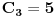 , Katalanov broj, i on uračunava zagrade). Naravno, stvarni broj različitih rezultata je dosta manji (pre svega, neki od dobijenih izraza su ekvivalentni, a i možda i neki drugi daju isti rezultat), ali i ovo je dovoljno da se začas (računarom) testira može li se dobiti traženi broj. Štaviše, program dole (pisan u programskom paketu Mathematica) pronalazi sva rešenja: ima ih ukupno , Katalanov broj, i on uračunava zagrade). Naravno, stvarni broj različitih rezultata je dosta manji (pre svega, neki od dobijenih izraza su ekvivalentni, a i možda i neki drugi daju isti rezultat), ali i ovo je dovoljno da se začas (računarom) testira može li se dobiti traženi broj. Štaviše, program dole (pisan u programskom paketu Mathematica) pronalazi sva rešenja: ima ih ukupno 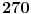 (računajući i (računajući i  ), i među njima nema broja ), i među njima nema broja 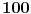 (štaviše, najveći rezultat je (štaviše, najveći rezultat je 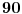 , a najmanji , a najmanji  ). ).Code: Module[{Operacije, Permutacije, i, j, k, p, a, b, c, d, op1, op2, op3}, Resenja = {}; Operacije = {"+", "-", "*", "/"}; Permutacije = Permutations[{"5", "2", "3", "3"}]; For[i = 1, i <= 4, i++, For[j = 1, j <= 4, j++, For[k = 1, k <= 4, k++, For[p = 1, p <= Length[Permutacije], p++, a = Permutacije[[p, 1]]; b = Permutacije[[p, 2]]; c = Permutacije[[p, 3]]; d = Permutacije[[p, 4]]; op1 = Operacije[[i]]; op2 = Operacije[[j]]; op3 = Operacije[[k]]; Resenja = Join[Resenja, { ToExpression[ StringJoin["((", a, op1, b, ")", op2, c, ")", op3, d]], ToExpression[ StringJoin["(", a, op1, "(", b, op2, c, "))", op3, d]], ToExpression[ StringJoin["(", a, op1, b, ")", op2, "(", c, op3, d, ")"]], ToExpression[ StringJoin[a, op1, "((", b, op2, c, ")", op3, d, ")"]], ToExpression[ StringJoin[a, op1, "(", b, op2, "(", c, op3, d, "))"]] }] ] ] ] ]; Resenja = Union[Resenja] ] Onda mi je palo na pamet da je autor zadatka možda prihvata i (unarnu) operaciju negacije. No, svaki tako dobijen broj već bi se morao nalaziti na dobijenom spisku, eventualno sa suprotnim znakom. Kako smo već konstatovali da je najmanji broj koji smo dobili  , ni s ovim dodatkom ne možemo premašiti , ni s ovim dodatkom ne možemo premašiti 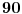 . Dodajmo samo da se u ovom slučaju dostiže . Dodajmo samo da se u ovom slučaju dostiže  različitih rešenja. različitih rešenja.[ strimad @ 14.08.2008. 10:56 ] @
Mozda nije dekadni sistem
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|