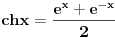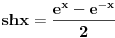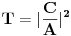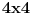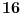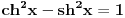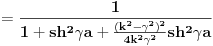[ Nemanjich @ 15.07.2008. 19:36 ] @
| Vecina,verovatno svi, identiteti "obicne" trigonometrije mogu se izvesti pomocu Ojlerove formule e^(iy)=cosy + isiny. Ne znam da li ova formula u ovom obliku e^(-x)= chx+ i shx, za y=ix(mozda je ovde greska) sme da se koristi u izvodjenju hiperbolickih identiteta , ali ja nikako ne mogu da dokazem da je ch2x=(chx)^2+ (shx)^2, ono sto dobijem je ch2x=(chx)^2- (shx)^2=1 sto nikako ne moze. Da li moze neko da pomogne? (valjda nigde nisam napravio neku gresku). |