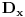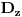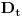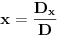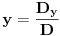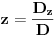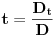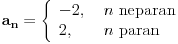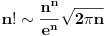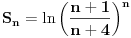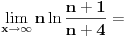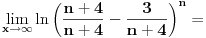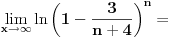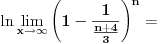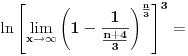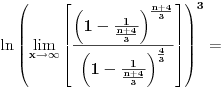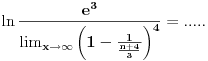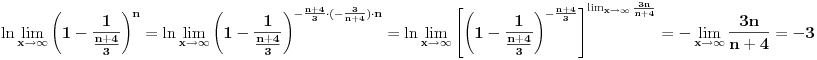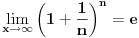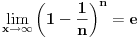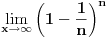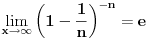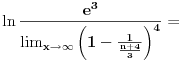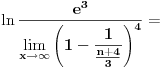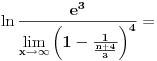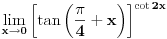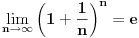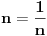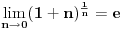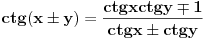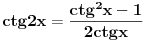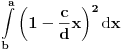[ R A V E N @ 15.07.2008. 20:16 ] @
|
[ petarm @ 15.07.2008. 20:21 ] @
Citat: R A V E N: Drugo pitanje je vezano sa relacije:da li simbol simbol  predstavlja relaciju ekvivalencije(u nekim knjgama se on naziva "indentički jednako")?A šta predstavlja simbol predstavlja relaciju ekvivalencije(u nekim knjgama se on naziva "indentički jednako")?A šta predstavlja simbol 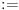 ? ?Da predstavlja! 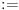 - dodela vrednosti - dodela vrednosti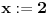  -u sam dodelio vrednost 2 -u sam dodelio vrednost 2[ Bojan Basic @ 15.07.2008. 21:20 ] @
Citat: R A V E N: Rješenja koja se dobiju su  , ,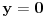 , ,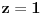 i i 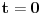 što izgleda tačno,ali ako npr. uzmemo što izgleda tačno,ali ako npr. uzmemo 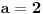 dobiva se dobiva se 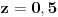 i očigledno postoji problem.Zašto se metoda determinanti ne može primjeniti ovdje? i očigledno postoji problem.Zašto se metoda determinanti ne može primjeniti ovdje?Može se primeniti (i dobro si ga primenio), ali ne možeš fiksirati neku vrednost parametra  kakvu ti hoćeš, već kakvu ti hoćeš, već  mora da ostane parametar (tj. nepoznate se moraju izraziti preko njega). Nakon što to izračunaš, lepo kažeš: „Sistem je saglasan za mora da ostane parametar (tj. nepoznate se moraju izraziti preko njega). Nakon što to izračunaš, lepo kažeš: „Sistem je saglasan za 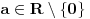 , i tada rešenja iznose...“. , i tada rešenja iznose...“.[ boolander @ 16.07.2008. 00:50 ] @
btw, := znači da je desna strana po definiciji jednaka levoj
[ Nedeljko @ 16.07.2008. 12:28 ] @
@RAVEN
Jedna ispravka. Sistem može imati determinantu jednaku nuli i biti saglasan. Taj slučaj nastupa kada sistem ima beskonačno mnogo rešenja. Determinanta je različita od nule ako i samo ako sistem ima tačno jedno rešenje. Znači, kada je determinanta različita od nule (u tvom slučaju 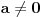 ) ima[ tačno jedno rešenje koje možeš izraziti preko determinanti (pri čemu svi parametri ostaju parametri). Kada je determinanta jednaka nuli (kod tebe slučaj ) ima[ tačno jedno rešenje koje možeš izraziti preko determinanti (pri čemu svi parametri ostaju parametri). Kada je determinanta jednaka nuli (kod tebe slučaj 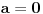 ), pošto znaš tačnu vrednost parametra, zameniš ga pa rešavaš sistem. ), pošto znaš tačnu vrednost parametra, zameniš ga pa rešavaš sistem.[ R A V E N @ 16.07.2008. 13:59 ] @
Citat: Nedeljko:Sistem može imati determinantu jednaku nuli i biti saglasan.Taj slučaj nastupa kada sistem ima beskonačno mnogo rešenja. U mojoj literaturi takav sistem se naziva neodređenim a saglasnim se naziva onaj koji striktno ima 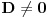 ,bez obzira na vrijednosti determinanti nepoznatih.Ali možda se,ako se opštije gleda,i neodređen sistem može nazvati saglasnim. ,bez obzira na vrijednosti determinanti nepoznatih.Ali možda se,ako se opštije gleda,i neodređen sistem može nazvati saglasnim.Citat: Nedeljko:Kada je determinanta jednaka nuli (kod tebe slučaj ), pošto znaš tačnu vrednost parametra, zameniš ga pa rešavaš sistem. Misliš na to da onda mogu za  uzeti proizvoljnu vrijednost iz uzeti proizvoljnu vrijednost iz 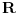 osim osim  ? ?Citat: Bojan Basic:„Sistem je saglasan za 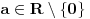 , i tada rešenja iznose...“. , i tada rešenja iznose...“.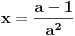 , ,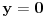 , ,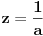 i i 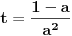 . .Evo teoretska nadopuna o tzv. trećem slučaju u primjeru nehomogenog sistema sa tri jednačine i sa tri nepoznate: 3.Ako je 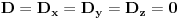 tada mogu nastupiti slijedeći slučajevi: tada mogu nastupiti slijedeći slučajevi:a)ako su sve subdeterminante determinante sistema  (ima ih 9) jednake nuli,onda slijedi da su koeficijenti uz nepoznate proporcionalni,pa mogu nastupiti slijedeća dva slučaja: (ima ih 9) jednake nuli,onda slijedi da su koeficijenti uz nepoznate proporcionalni,pa mogu nastupiti slijedeća dva slučaja:1)ako su i nezavisni članovi sistema jednačina proporcionalni koeficijentima uz nepoznate,onda je takav sistem neodređen i ima beskonačno mnogo rješenja,a jednačine su zavisne. 2)ako nezavisni članovi sistema jednačina nisu proporcionalni sa koeficijentima uz nepoznate,onda sistem jednačina nema rješenje,a za jednačine kažemo da su protivriječne. b)da je bar jedna od devet subdeterminanata determinante sistema  različita od nule,onda je sistem jednačina neodređen i ima beskonačno mnogo rješenja,a za jednačine kažemo da su zavisne. različita od nule,onda je sistem jednačina neodređen i ima beskonačno mnogo rješenja,a za jednačine kažemo da su zavisne.[Ovu poruku je menjao R A V E N dana 16.07.2008. u 16:20 GMT+1] [ Nedeljko @ 16.07.2008. 14:14 ] @
Baš čudna literatura. Saglasnost bi morala da bude suprotan pojam od protivrečnosti. No, OK. Drži se definicija profesora kod koga polažeš ispit.
[ R A V E N @ 16.07.2008. 15:31 ] @
Da,stavka 2) je zbunjujuća.
[ Bojan Basic @ 16.07.2008. 16:06 ] @
Citat: R A V E N: b)da je bar jedna od devet subdeterminanata determinante sistema  različita od nule,onda je sistem jednačina neodređen i ima beskonačno mnogo rješenja,a za jednačine kažemo da su zavisne. različita od nule,onda je sistem jednačina neodređen i ima beskonačno mnogo rješenja,a za jednačine kažemo da su zavisne.Ovo ni slučajno nije tačno. U tom slučaju sistem nema rešenja, tj. jednačine su protivrečne — isto kao pod a2). [ R A V E N @ 16.07.2008. 21:29 ] @
U redu.Knjiga je Mr. Branislav Stojanović - Zbirka zadataka iz matematike iz 1981.,napravljena od tuzlanskog profesora...odprilike po Apsenovom kursu.
[ h4su @ 16.07.2008. 21:30 ] @
Citat: Bojan Basic: Ovo ni slučajno nije tačno. U tom slučaju sistem nema rešenja, tj. jednačine su protivrečne — isto kao pod a2). To je tacno a vidi se na primjeru 2x+3y-4z=2,x+y+3z=3,3x+4y-z=5.Posljednja jednakost se dobije kad se saberu prve dvije a vrijedi D=Dx=Dy=Dz a je sistem neodredjen i ima beskonacno mnogo rjesenja. [Ovu poruku je menjao h4su dana 16.07.2008. u 22:43 GMT+1] [ Bojan Basic @ 16.07.2008. 21:49 ] @
Citat: h4su: ...a vrijedi D=Dx=Dy=Dz... A sad pročitaj deo Ravenove poruke koji sam citirao (i koji sam komentarisao). [ miki069 @ 16.07.2008. 21:49 ] @
Citat: "3.Ako je tada mogu nastupiti slijedeći slučajevi:
a)ako su sve subdeterminante determinante sistema (ima ih 9) jednake nuli,onda slijedi da su koeficijenti uz nepoznate proporcionalni,pa mogu nastupiti slijedeća..." Ako je D = Dx = Dy = Dz = Dt = ... = 0 onda Kremerova teorema nema odluku da li sistem ima beskonacno mnogo resenja (sto je najcesci ishod) ili ipak sistem nema resenja? Nego kao sto ti je receno: 1. Znas za koju vrednost parametra a se to desilo. 2. Zamenis tu vrednost parametra u sistem i taj slucaj uradis (posle Gausovog metoda eliminacije) primenom Kroneker-Kapelijeve teoreme. Petljanje sa subdeterminantama (minorima) je pasji posao. Tvoj sistem ima 16 minora tipa 3X3. Koliko vremena treba da se svi oni izracunaju? Mnogooo. Pravilo: posmatraj izraze za D, Dx, Dy, Dz i Dt kao polinome (sto i jesu) od parametra a. Vazi 100% sledeca (Miki069) Teorema: 1. ako je ta sporna vrednost parametra a istostruka nula (najcesce obicna jednostruka nula) svim tim polinomima onda sistem ima beskonacno mnogo resenja. 2. ako je ta sporna vrednost parametra a nula viseg reda za polinom glavne determinante D od bar jedne od Dx ili Dy ili Dz ili Dt onda sistem nema resenja. U tvom primeru polinom D=2*a^2 ima a1=a2=0 dvostruku nulu a=0. To a=0 je obicna (jednostruka) nula polinomu Dx. Sigurno i polinomu Dz (ali nije bitno). Ispunjeni su uslovi stava 2 Miki069 Teoreme i sledi da sistem nema resenja. Jasno da ti taj zakljucak niko ne bi priznao na osnovu Miki069 Teoreme. Neko kako ti je vec receno: zameni a=0 u sistem i Gausovim metodom eliminacije pokazi da rang(A) nije jednak rangu(Ap) i da sistem za a=0 nema resenje po Kroneker-Kapelijevoj a ne po Miki069 teoremi. Ako treba dokaz Miki069 teoreme izlozicu ga. Mada pisem knjigu i bice obavezno u njoj. Evo ti jedan sistem koji je dosta poucan i cesto pada na ispitima: aX + Y + Z = 1 X + aY +Z = 2 X + Y + aZ = -3 Glavna determinanta D ima nule a1 = -2, a2 = 1 i a3 = 1. Sve ostale determinante imaju nule a1 = -2 i a2 = 1. Za a = -2 (posto je jednostruka nula glavnoj determinanti i svim drugim) po Miki069 Te sistem ima beskonacno mnogo resenja. Za a = 1 (posto je dvostruka nula glavnoj determinanti a jednostruka Dx i svim drugim) po Miki069 Te sistem nema resenje. Za a = - 2 Miki069 Te ti ne moze pronaci tih beskonacno mnogo resenja. Samo garancija da ih ima. Gausov metod eliminacije ti ne samo da priprema uslove za primenu KronekerKapelije teoreme vec ti priprema i sistem za pronalazenje tih resenja. Dakle zamenis a = -2 u sistem i Gausov metod i to je to. Isto tako i slucaj a = 1. Zbirku (ne knjigu) sam vec rekao Milic-Uscumlic i nista drugo (ima 5 000 zadataka). Za ekstremno bavljenje matematikom Mitrinovic. Pozdrav [Ovu poruku je menjao miki069 dana 16.07.2008. u 23:04 GMT+1] [ h4su @ 16.07.2008. 22:13 ] @
Citat: Bojan Basic: A sad pročitaj deo Ravenove poruke koji sam citirao (i koji sam komentarisao). Ovo je napisao RAVEN: 3.Ako je tada mogu nastupiti slijedeći slučajevi: a)ako su sve subdeterminante determinante sistema (ima ih 9) jednake nuli,onda slijedi da su koeficijenti uz nepoznate proporcionalni,pa mogu nastupiti slijedeća dva slučaja: 1)ako su i nezavisni članovi sistema jednačina proporcionalni koeficijentima uz nepoznate,onda je takav sistem neodređen i ima beskonačno mnogo rješenja,a jednačine su zavisne. 2)ako nezavisni članovi sistema jednačina nisu proporcionalni sa koeficijentima uz nepoznate,onda sistem jednačina nema rješenje,a za jednačine kažemo da su protivriječne. b)da je bar jedna od devet subdeterminanata determinante sistema različita od nule,onda je sistem jednačina neodređen i ima beskonačno mnogo rješenja,a za jednačine kažemo da su zavisne. Ovo si napisao ti: Citat: Bojan Basic: Ovo ni slučajno nije tačno. U tom slučaju sistem nema rešenja, tj. jednačine su protivrečne — isto kao pod a2). Ovo sam napisao ja manje vise u stvari je primjer iz te iste zbirke 2x+3y-4z=2,x+y+3z=3,3x+4y-z=5. Sad mi reci jel i dalje ostajes pri onom sto si rekao. Pozdrav [ miki069 @ 16.07.2008. 23:08 ] @
Druze ovaj tvoj sistem ima beskonacno mnogo resenja.
rang(A) = rang(Ap) = 2. Bazisni minor je formata 2X2. Ima u sebi 2 vrste (jednacine) i 2 kolone (nepoznate). Gausovim metodom je pokazano da je treca jadnacina linearno zavisna od prve i druge. Viska je recimo ona kao vrsta. Viska je jedna nepoznata (recimo Z) koja se prebaci na desnu stranu. Y = 10*Z - 4. Posle se iz prve dobije X =.... Ovakav sistem se ne moze uraditi (naci mu tih beskonacno resenja) primenom nekih produzetaka Kramerove Teoreme koje je RAVEN iznosio. Ovaj primer pokazuje da su ti RAVENOVI produzeci ispravno koncipirani. Cak ne moze naci resenje ni preko briljantne Miki069 Teoreme. Samo se moze zakljuciti da ih ima beskonacno mnogo. Gausov metod eliminacije pa onda Kroneker-Kapelije teorema koja je opet nedorecena (u delu kada kaze sistem je saglasan - ona sama nema odluku jeli jedinstveno resenje ili beskonacno mnogo resenja) bez Teoreme o Bazisnom minoru primenjene na matricu Ap. Pozdrav h4su. Daj neku kosku iz kombinatorike. Video sam da ste Srki, Kecman i ti experti za to. Ja sam tamo bio prolupo jedno 3-4 puta zesce. Pozdrav jos jednom [Ovu poruku je menjao miki069 dana 17.07.2008. u 00:20 GMT+1] [ R A V E N @ 17.07.2008. 01:01 ] @
Nešto iz teorije skupova:kakav je to amorfan skup?
[ petarm @ 17.07.2008. 03:42 ] @
Amorfni skup je skup koji se dobija zanemarivanjem strukture nekog matematickog objekta ako se ne varam? Sta ce ti to?
[ R A V E N @ 21.07.2008. 19:46 ] @
U knjizi po kojoj mi učimo matematiku spominje se takav skup:"Skupove označavamo velikim slovima
 , , , , , , , , , , , , ,dok elemente amorfnog skupa označavamo najčešće malim slovima." i to u negdje u 3 ili 4 rečenici od početka poglavlja o skupovima. ,dok elemente amorfnog skupa označavamo najčešće malim slovima." i to u negdje u 3 ili 4 rečenici od početka poglavlja o skupovima.Znači zanemaruju se osobine tih elemenata koji sačinjavaju skup i jedino što se kod njih uzima za bitno je da su članovi tog skupa i ništa više? [Ovu poruku je menjao R A V E N dana 21.07.2008. u 21:01 GMT+1] [ R A V E N @ 11.08.2008. 13:58 ] @
[ MathManiac @ 11.08.2008. 21:56 ] @
[ Bojan Basic @ 11.08.2008. 22:52 ] @
Citat: R A V E N: Je li ovo moje tačno? Jeste tačno. Ne mogu se složiti s mišljenjem koje je izneo MathManiac, jer nije dužnost rešavača da gleda u pasulj kako bi saznao šta je postavljač zadatka mislio i da li podrazumeva formulu u „sirovom“ značenju (šta god to bilo). [ MathManiac @ 12.08.2008. 01:06 ] @
Konstrukcija koju sam zapisao, kao i ono tvoje, je trivijalno rješenje. U biti, i nije rješenje već samo matematičkim simbolima prepisan zadatak. Svakako se potrudi dobiti formulu za opći član jer je to rješenje. Maloprije sam popio kavu i zavirio u šoljicu; tamo tako isto piše. :-)
[ R A V E N @ 12.08.2008. 05:37 ] @
MathManiac je koristio zapis za funkciju,a i niz je zapravo samo jedna funkcija.
Zapis niza u dvije formule(jedna za parne,druga za neparne članove) je meni bio neobičan izprva,ali se koristi u zbirci Miličić-Ušćumlić. [ Bojan Basic @ 12.08.2008. 11:59 ] @
Citat: MathManiac: Konstrukcija koju sam zapisao, kao i ono tvoje, je trivijalno rješenje. U biti, i nije rješenje Trivijalno rešenje nije rešenje? Ponoviću, zadatak je postavljača da se obezbedi od trivijalnih rešenja (ako mu se ona ne dopadaju). U ovom slučaju bilo je dovoljno npr. tražiti niz čiji su svi članovi međusobno različiti (a to nije traženo). Da li vaš niz zadovoljava postavljene uslove (da su mu  i i 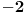 tačke nagomilavanja) — zadovoljava. Na osnovu čega onda neko može tvrditi da to nije tačno rešenje? tačke nagomilavanja) — zadovoljava. Na osnovu čega onda neko može tvrditi da to nije tačno rešenje? [ h4su @ 12.08.2008. 14:04 ] @
Citat: R A V E N: Code: Problem 4. Napisati opšti član niza koji ima tačke nagomilavanja 2 i -2. Ja napišem: -neparni članovi: 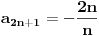 -parni članovi: 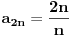 međutim,ponuđeno rješenje je 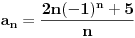 . .Je li ovo moje tačno? To sto si ti napisao je ustvari ovo 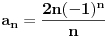 ,sto si i sam mogao skontat. ,sto si i sam mogao skontat.[ MathManiac @ 12.08.2008. 14:14 ] @
Tijekom mog studija matematike je bilo pravilo da se opći član niza piše kao zatvorena formula, a ne kao razlomljena.
Na koncu, opći član niza koji ima gomilišta 1 i -1 (redovit primjer u udžbenicima matematičke analize) se uvijek piše ovako 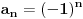 , a nikada ovako , a nikada ovako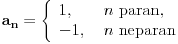 Barem ja nisam vidio da je neki autor to tako zapisao... [ R A V E N @ 14.08.2008. 14:53 ] @
h4su,dobro si to opazio(znači to riješiti zadatak elegantno?
Code: Problem 5: Izračunati : 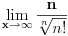 Trebam uputu - kako krenuti? [Ovu poruku je menjao R A V E N dana 14.08.2008. u 16:19 GMT+1] [ Kolins Balaban @ 14.08.2008. 15:39 ] @
mozda bi se mogla iskoristiti i Stolz-ova teorema.
[ R A V E N @ 14.08.2008. 18:05 ] @
Vjerovatno su na Stolzovu mislili,Stirlingov obrazac mi izgleda too advanced za naš nivoo,mada znam i za njega.
[ R A V E N @ 20.08.2008. 12:21 ] @
Code: Problem 6: Ako je zadato 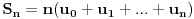 gdje je gdje je 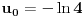 a a 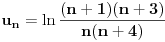 ,izračunati ,izračunati 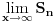 .Uščumlić 1591. .Uščumlić 1591.Ako primjenim formulu za zbir prvih  članova aritmetičkog niza i izvršim zamjenu za članova aritmetičkog niza i izvršim zamjenu za 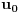 dobijam dobijam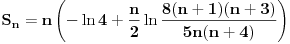 i nakon niza transformacija(operacije s logaritmima) izađem na 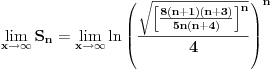 što ja ne znam da izračunam. U rješenju se tvrdi da se izraz 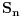 zapravo svede na zapravo svede na 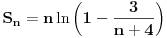 i da je njegov limes i da je njegov limes 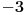 . .Kako je sveden na ovaj izraz i gdje sam ja pogriješio? [Ovu poruku je menjao R A V E N dana 20.08.2008. u 15:19 GMT+1] [ petarm @ 20.08.2008. 13:20 ] @
Citat: R A V E N: Code: Problem 5: Izračunati : 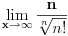 [Ovu poruku je menjao R A V E N dana 14.08.2008. u 16:19 GMT+1] Samo ovde umesto  stavi stavi  [ petarm @ 20.08.2008. 13:24 ] @
Citat: R A V E N: Vjerovatno su na Stolzovu mislili,Stirlingov obrazac mi izgleda too advanced za naš nivoo,mada znam i za njega. Mislim da nisi u pravu! Ovde je mnogo lakse upotrebiti Stirlingovu aproksimaciju! [ R A V E N @ 20.08.2008. 13:32 ] @
Kasno je sad za ispravku.
[ Gn0m3 @ 20.08.2008. 14:14 ] @
Hajde da pokušamo da razbijemo opšti član un.
Koristeći osobine ln f-je uočavamo da je: un = ln (n+1) + ln (n+3) - ln (n) - ln (n+4) Sada, krucijalno je iskoristiti ono što je meni asistent iz Analize sve vreme ponavaljao - kad god imate niz, pokušajte izračunati prvih nekoliko članova čisto da "osetite" kako se niz ponaša. Elem, u0 = -ln 4 u1 = ln 2 + ln 4 - ln 1 - ln 5 u2 = ln 3 + ln 5 - ln 2 - ln 6 u3 = ln 4 + ln 6 - ln 3 - ln 7 u4 = ln 5 + ln 7 - ln 4 - ln 8 ... un = ln(n+1) + ln(n+3) - ln(n) - ln(n+4) Kada počneš da sabiraš ove članove uočićeš da je reč o tzv. "teleskopskoj" sumi (skoro će se svi članovi pokratiti) te konačno u0 + u1 + ... + un = ln (n+1) - ln (n + 4) a verujem da odavde i sam možeš naći traženo rešenje... Sve najbolje. [ Kolins Balaban @ 20.08.2008. 14:28 ] @
[ R A V E N @ 20.08.2008. 19:08 ] @
Računanje prvih nekoliko članova mi je djelovalo kao više nagađanje,uvijek je moguće da recimo 50-i član drugačije izgleda,ali to bi bilo to,"tnx"!
[ R A V E N @ 21.08.2008. 15:48 ] @
[ Bojan Basic @ 21.08.2008. 17:58 ] @
[ R A V E N @ 23.08.2008. 11:59 ] @
[ R A V E N @ 23.08.2008. 21:05 ] @
[ Kolins Balaban @ 23.08.2008. 22:18 ] @
[ R A V E N @ 23.08.2008. 22:38 ] @
Ali ako ne bih odradio l`Hopitalovim pravilom,vjerovatno bi na pregledu ispita od mogućih 20 ubrojili samo 10 poena...plus još kad "oporezuju" one mikrogreškice.
 [ R A V E N @ 05.09.2008. 03:53 ] @
[ Kolins Balaban @ 05.09.2008. 08:13 ] @
izracunas dati integral kao neodredjeni, a onda primjenis Njutn-Lajbnicovu formulu za izracunavanje odredjenog integrala.
pogledaj ovo malo: http://www.fer.hr/_download/repository/C8PrimjenaIntegrala.pdf [ R A V E N @ 05.09.2008. 13:27 ] @
Znam za uvrštavanje i oduzimanje granica nakon što se izračuna integral(a.k.a. NL formula),samo nisam znao da izračunam podintegralni izraz,hajde pročitaću to.
[ Kolins Balaban @ 05.09.2008. 14:45 ] @
pa samo kvadriras podintegralnu velicinu, i rezultat toga rastavis na vise integrala, ha ya :)
[ R A V E N @ 05.09.2008. 18:28 ] @
[ igorpet @ 05.09.2008. 21:16 ] @
Citat: Kolins Balaban: pa samo kvadriras podintegralnu velicinu, i rezultat toga rastavis na vise integrala, ha ya :) Ili ovako ili smenom: 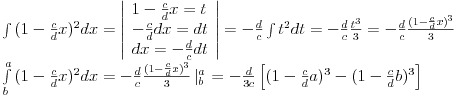 [ R A V E N @ 07.09.2008. 07:22 ] @
Citat: R A V E N: Kvadriram kao najobičniji kvadrat razlike,tri člana pomnožim sa diferencijalom od  i sve se raspadne na tri integrala koja onda riješim - probao sam i tako,ali dobijem netačan rezultat u finalnom rješenju(ovo je samo segment zadatka),ali ako može i tako,onda u redu.:) i sve se raspadne na tri integrala koja onda riješim - probao sam i tako,ali dobijem netačan rezultat u finalnom rješenju(ovo je samo segment zadatka),ali ako može i tako,onda u redu.:)Riješeno,primjena je bila u redu,ali je bilo par grešaka. [ malada @ 15.09.2008. 17:07 ] @
Sto se tice rekurzivno zadatih nizova, najlaksi nacin koji sam ja nasao dok sam spremao Analizu I je pomocu funkcija tj posmatras pridruzenu f-ju i u zavisnosti od monotonosti te f-je dobijas 2 slucaja. Ako neko ima vremena neka ispise citav postupak, ako ne ispisacu ja kad nadjem vremena.
Pozdrav [ R A V E N @ 26.10.2008. 10:57 ] @
Code: Problem 9: Zašto je ovaj integral nerješiv analitičkim putem: 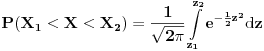 ( 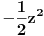 je u eksponentu od je u eksponentu od  ). ).Izraz potječe iz teorije tretiranja grešaka pri mjerenju u fizici i izvodi se na osnovu Gaussove funkcije raspodjele slučajnih varijabli: 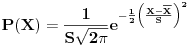 na osnovu čega se dobiva da je vjerovatnoća da je neka vrijednost mjerenja  u intervalu u intervalu 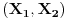 : :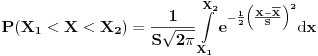 i uvođenjem transformacija: 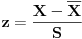 i i 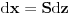 dobija se gornji prvi izraz. [Ovu poruku je menjao R A V E N dana 26.10.2008. u 13:12 GMT+1] Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|