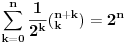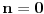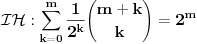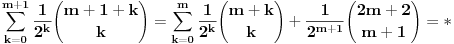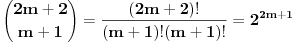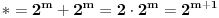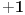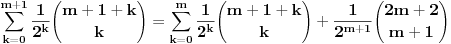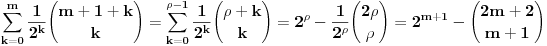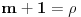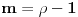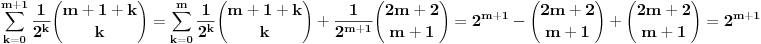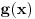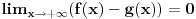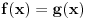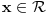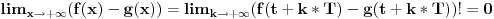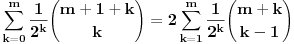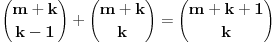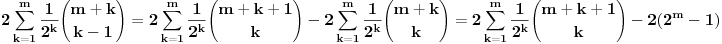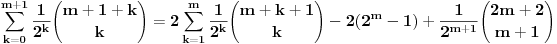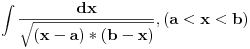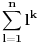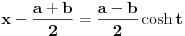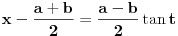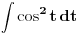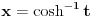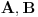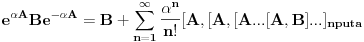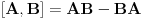[ petarm @ 17.07.2008. 00:24 ] @
|
[ h4su @ 17.07.2008. 11:27 ] @
Moze matematickom indukcijom lako da se rjesi.
[ Nedeljko @ 17.07.2008. 12:35 ] @
[ petarm @ 17.07.2008. 17:02 ] @
Citat: h4su: Moze matematickom indukcijom lako da se rjesi. To je jasno! Moze li bez nje? Neko originalno resenje?! Citat: Nedeljko: Dokazati da je prvih  cifara iza decimalne tacke u zapisu broja cifara iza decimalne tacke u zapisu broja 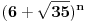 jednako 9. jednako 9.Resenje je elegantno i dokumentovano na ovom forumu. Ovakve stvari su nepotrebne za bilo sta u nekoj praksi i zivotu pa se ne bih udubljivao! Ko ovo voli da radi iz hobija super! [ Bojan Basic @ 18.07.2008. 15:55 ] @
Hajde da probam Petrov zadatak (ovaj koji je Nedeljko izneo sam upravo ja svojevremeno postavio na forum, pa nema smisla da opet pišem isto rešenje
Pođimo od identiteta 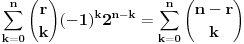 , za koji se lako vidi da važi za , za koji se lako vidi da važi za 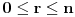 (tada su obe strane jednake (tada su obe strane jednake 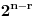 ), ali kako obe strane predstavljaju polinom po ), ali kako obe strane predstavljaju polinom po  stepena najviše stepena najviše  , i kako se poklapaju u , i kako se poklapaju u  tački, sledi da identitet važi uvek. Stavljajući sada tački, sledi da identitet važi uvek. Stavljajući sada 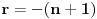 ostaje ostaje 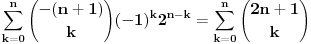 . Leva strana je jednaka . Leva strana je jednaka 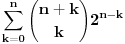 a desna predstavlja zbir prve polovine elemenata a desna predstavlja zbir prve polovine elemenata 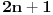 -og reda Paskalovog trougla, a kako su oni (zbog simetričnosti Paskalovog trougla) jednaki drugoj polovini, zbir na desnoj strani iznosi -og reda Paskalovog trougla, a kako su oni (zbog simetričnosti Paskalovog trougla) jednaki drugoj polovini, zbir na desnoj strani iznosi 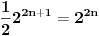 Deljenjem obeju strana sa Deljenjem obeju strana sa 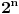 imamo identitet koji je trebalo dokazati. imamo identitet koji je trebalo dokazati.Pao mi je na pamet i neki kombinatorni argument, ali o tom potom, kad proverim koliko to ima smisla. Naravno, bilo bi lepo zabeležiti i rešenje indukcijom, ali to bih prepustio nekom drugom. [Ovu poruku je menjao Bojan Basic dana 11.03.2009. u 15:41 GMT+1] [ petarm @ 19.07.2008. 00:15 ] @
[ Bojan Basic @ 19.07.2008. 01:55 ] @
[ Bojan Basic @ 19.07.2008. 12:55 ] @
Dobro, ali sad ne možeš primeniti indukcijsku hipotezu.
[ Farenhajt @ 19.07.2008. 21:08 ] @
Dokaz prvog zadatka preko verovatnoće:
Bacajmo novčić 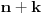 puta. Tada izraz puta. Tada izraz 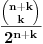 predstavlja verovatnoću da u eksperimentu dobijemo predstavlja verovatnoću da u eksperimentu dobijemo  ishoda jedne vrste i ishoda jedne vrste i  ishoda druge vrste. Eksperiment smatramo uspešnim ako se pojavilo ishoda druge vrste. Eksperiment smatramo uspešnim ako se pojavilo  ishoda jedne vrste. To će se sigurno desiti posle najviše ishoda jedne vrste. To će se sigurno desiti posle najviše  bacanja (a eventualno i ranije). Dakle, sumiranjem navedenih izraza po bacanja (a eventualno i ranije). Dakle, sumiranjem navedenih izraza po  , u granicama od , u granicama od  do do  , dobijamo siguran događaj, te suma iznosi , dobijamo siguran događaj, te suma iznosi  . Rezultat sledi. . Rezultat sledi.EDIT: Desiće se, zapravo, posle 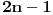 bacanja, po Dirihleu. Gde mi je greščica? bacanja, po Dirihleu. Gde mi je greščica?[ Bojan Basic @ 19.07.2008. 23:22 ] @
Citat: Ovo je dvosmisleno: jesi li unapred fiksirao šta ti je jedna a šta druga vrsta, ili ti je pak bitno samo da odnos bude takav, bez obzira na to šta je šta? Ispravan je prvi rezon, tj. da kažemo „...dobijemo  pisama i pisama i  glava“, a ovo naglašavam zato što mi izgleda da si naknadno prešao na drugo tumačenje. glava“, a ovo naglašavam zato što mi izgleda da si naknadno prešao na drugo tumačenje.Svejedno, posle praviš mnogo veću grešku: Citat: Ovo ne možeš sumirati, jer su opiti različiti (bacaš 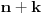 novčića, a novčića, a  je promenljivo). je promenljivo).[Ovu poruku je menjao Bojan Basic dana 20.07.2008. u 03:28 GMT+1] [ Farenhajt @ 20.07.2008. 01:00 ] @
A ovakvo tumačenje, recimo?
Stavimo  belih i belih i  crnih kuglica u kutiju, pa nasumično izvučemo crnih kuglica u kutiju, pa nasumično izvučemo  kuglica. Eksperiment je "izvući sve bele kuglice", a nakon prvih kuglica. Eksperiment je "izvući sve bele kuglice", a nakon prvih  izvlačimo jednu po jednu dok se eksperiment ne okonča - a sigurno će se okončati najdalje do izvlačimo jednu po jednu dok se eksperiment ne okonča - a sigurno će se okončati najdalje do  -te kuglice. -te kuglice.EDIT: Tu je možda problem nezavisnost daljih izvlačenja. U tom slučaju, možda može ovako: Izvučemo 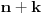 kuglica i konstatujemo jesu li među njima zastupljene sve bele. Ako nisu, vraćamo kuglice u kutiju i ponovo vadimo izvestan broj. kuglica i konstatujemo jesu li među njima zastupljene sve bele. Ako nisu, vraćamo kuglice u kutiju i ponovo vadimo izvestan broj.[ petarm @ 20.07.2008. 02:44 ] @
[ petarm @ 20.07.2008. 03:33 ] @
[ h4su @ 20.07.2008. 12:39 ] @
[ Bojan Basic @ 20.07.2008. 14:27 ] @
Citat: Farenhajt: Stavimo  belih i belih i  crnih kuglica u kutiju, pa nasumično izvučemo crnih kuglica u kutiju, pa nasumično izvučemo  kuglica. Eksperiment je "izvući sve bele kuglice", a nakon prvih kuglica. Eksperiment je "izvući sve bele kuglice", a nakon prvih  izvlačimo jednu po jednu dok se eksperiment ne okonča - a sigurno će se okončati najdalje do izvlačimo jednu po jednu dok se eksperiment ne okonča - a sigurno će se okončati najdalje do  -te kuglice. -te kuglice.Ajd za nezavisnost, ali pri ovakvom eksperimentu nemaš 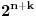 mogućih događaja. mogućih događaja.Citat: Ne, naravno. Kada radiš nešto indukcijom, bitno je da prilikom pozivanja na indukcijsku hipotezu vrednost za koju je primenjuješ zaista bude manja od one s kojom tog momenta radiš — a ne samo da uvedeš smenu kako bi to tako izgledalo. :) U citiranom delu primenjuješ indukcijsku hipotezu za 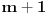 (kako god ti to zvao, a nazvao si (kako god ti to zvao, a nazvao si  ), što ne možeš. ), što ne možeš.[ petarm @ 20.07.2008. 15:22 ] @
[ petarm @ 20.07.2008. 20:03 ] @
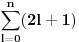  - fiksno - fiksno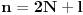 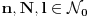 Ako je  parno ocigledno je i parno ocigledno je i  parno i ako je parno i ako je  neparno onda je i neparno onda je i  neparno! Pretpostavljam da je jedini nacin da pokazem kolko iznosi gornja suma je da pokazem kolko iznosi za neparno! Pretpostavljam da je jedini nacin da pokazem kolko iznosi gornja suma je da pokazem kolko iznosi za  parno, parno,  neparno i da pokazem da nema razlike? Voleo bih u svakom slucaju da vidim moze li se ovo ikako resiti drugacije? neparno i da pokazem da nema razlike? Voleo bih u svakom slucaju da vidim moze li se ovo ikako resiti drugacije? - parno - parno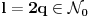 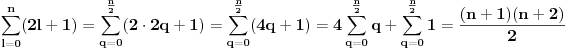  - neparno - neparno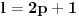 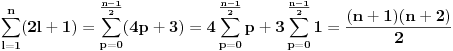 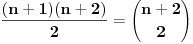 [Ovu poruku je menjao petarm dana 21.07.2008. u 13:30 GMT+1] [ petarm @ 21.07.2008. 00:28 ] @
Zao mi je sto nisam uspeo da isteram ovo sa indukcijom do kraja. Voleo bih da neko drugi istera ako ima vremena da vidim gde sam gresio. A ja bih se iskupio na sledeci nacin
Ja sam dokazao upravo jednu matematicku relaciju koja se cesto koristi u fizici pa sam resio da je okacim ovde racunajuci da ce se nekom svideti.Uz to bice i prica uz ovaj dokaz! To je operatorska relacija. U fizici se operatori pisu sa kapicom iznad slova ^ npr. 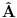 . To je uveo Landau (Nobelovac) kada je stigao u Moskvu. Stampari su u to vreme imali problema sa brojnim oznakama pa da bi im olaksao Landau je uveo da se operatori pisu na ovaj nacin.Fizicari tako pisu operatore i danas . To je uveo Landau (Nobelovac) kada je stigao u Moskvu. Stampari su u to vreme imali problema sa brojnim oznakama pa da bi im olaksao Landau je uveo da se operatori pisu na ovaj nacin.Fizicari tako pisu operatore i danas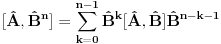 Gde je 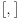 komutator (operatori su nekomutativne strukture) sa sledecim osobinama komutator (operatori su nekomutativne strukture) sa sledecim osobinamahttp://www.elitesecurity.org/t330663-Osobine-komutatora Ja cu pokusati da ovaj identitet dokazem matematickom indukcijom: 1.)  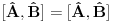 2.) 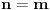  : :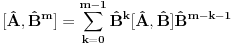 3.) 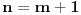 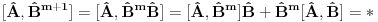 iskoristio sam jednu osobinu komutatora za koju vec postoji link u ovoj mojoj poruci 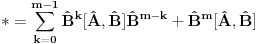 Poslednji sabirak je  -ti clan ove sume pa ga mogu uvuci pod sumu. Kada to uradim dobijam -ti clan ove sume pa ga mogu uvuci pod sumu. Kada to uradim dobijam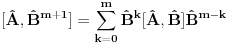 Cime je ovaj identitet dokazan. Ako nekog zanima naglasio bih jos zasto je ova relacija vazna u fizici! Za slucaj da 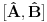 komutira sa komutira sa 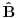 (naravno u tom slucaju komutira i sa svakim stepenom od (naravno u tom slucaju komutira i sa svakim stepenom od 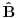 ) u zapisu ) u zapisu 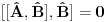 dobija se dobija se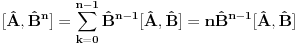 Posto se u kvantnoj mehanici postulira 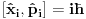 lako se dobija 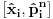 ili ili 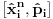 Nadam se da se ovo nekom svidelo! [ Nedeljko @ 21.07.2008. 08:30 ] @
Citat: petarm: 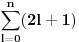  - fiksno - fiksno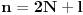 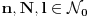 Ako je  parno ocigledno je i parno ocigledno je i  parno i ako je parno i ako je  neparno onda je i neparno onda je i  neparno! Pretpostavljam da je jedini nacin da pokazem kolko iznosi gornja suma je da pokazem kolko iznosi za neparno! Pretpostavljam da je jedini nacin da pokazem kolko iznosi gornja suma je da pokazem kolko iznosi za  parno, parno,  neparno i da pokazem da nema razlike? Voleo bih u svakom slucaju da vidim moze li se ovo ikako resiti drugacije? neparno i da pokazem da nema razlike? Voleo bih u svakom slucaju da vidim moze li se ovo ikako resiti drugacije?Prvo, 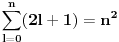 . Račun ti nije tačan. Ne znam odakle ti . Račun ti nije tačan. Ne znam odakle ti 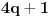 i i 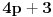 . A ako već znaš . A ako već znaš 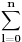 možeš ga odmah primeniti na možeš ga odmah primeniti na 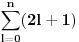 . .Jedan način je školska formula za zbir aritmetičke progresije: prvi član plus poslednji član ima isti zbir kao drugi plus pretposlednji itd. Drugi način je da se 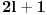 napiše kao napiše kao 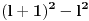 i onda ti se pokrate svi unutrašnji članovi. U vezi uopštenja ove ideje vidi i onda ti se pokrate svi unutrašnji članovi. U vezi uopštenja ove ideje vidihttp://www.elitesecurity.org/p1997028 [ petarm @ 21.07.2008. 12:39 ] @
Citat: petarm: 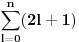  - fiksno - fiksno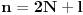 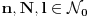 Ako je  parno ocigledno je i parno ocigledno je i  parno i ako je parno i ako je  neparno onda je i neparno onda je i  neparno! Pretpostavljam da je jedini nacin da pokazem kolko iznosi gornja suma je da pokazem kolko iznosi za neparno! Pretpostavljam da je jedini nacin da pokazem kolko iznosi gornja suma je da pokazem kolko iznosi za  parno, parno,  neparno i da pokazem da nema razlike? Voleo bih u svakom slucaju da vidim moze li se ovo ikako resiti drugacije? neparno i da pokazem da nema razlike? Voleo bih u svakom slucaju da vidim moze li se ovo ikako resiti drugacije? - parno - parno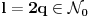 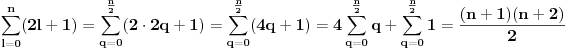  - neparno - neparno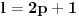 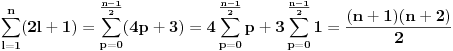 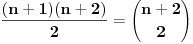 [Ovu poruku je menjao petarm dana 21.07.2008. u 13:30 GMT+1] Citat: Nedeljko: Prvo, 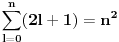 . Račun ti nije tačan. Ne znam odakle ti . Račun ti nije tačan. Ne znam odakle ti 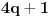 i i 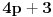 . A ako već znaš . A ako već znaš 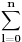 možeš ga odmah primeniti na možeš ga odmah primeniti na 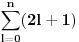 . .Jedan način je školska formula za zbir aritmetičke progresije: prvi član plus poslednji član ima isti zbir kao drugi plus pretposlednji itd. Drugi način je da se 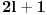 napiše kao napiše kao 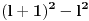 i onda ti se pokrate svi unutrašnji članovi. U vezi uopštenja ove ideje vidi i onda ti se pokrate svi unutrašnji članovi. U vezi uopštenja ove ideje vidihttp://www.elitesecurity.org/p1997028 Mozda se nisam najbolje izrazio, ali sam naglasio da izmedju 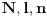 postoji veza. U zavisnosti od postoji veza. U zavisnosti od   ne moze da uzima sve vrednosti! Odnosno u jednom slucaju bi sumu bilo najbolje pisati kao ne moze da uzima sve vrednosti! Odnosno u jednom slucaju bi sumu bilo najbolje pisati kao , a u drugom , a u drugom  [ Nedeljko @ 21.07.2008. 13:30 ] @
Sad tek vidim šta si napisao. Ako je
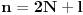 onda to onda to  ne može imati nikakve veze sa ne može imati nikakve veze sa  iz iz  , jer se prvo , jer se prvo  može zadavati (slobodno je), a drugo može zadavati (slobodno je), a drugo  trči preko nekih vrednosti i ne može biti zadano (vezano je). To je potpuno isto kao da si napisao trči preko nekih vrednosti i ne može biti zadano (vezano je). To je potpuno isto kao da si napisao 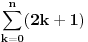 i ta suma je jednaka i ta suma je jednaka 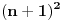 . Nisam baš čitao šta si sve napisao, ali se nadam da sam ti pomogao. . Nisam baš čitao šta si sve napisao, ali se nadam da sam ti pomogao.[ petarm @ 22.07.2008. 14:13 ] @
[ h4su @ 22.07.2008. 16:10 ] @
Obadvije sume idu do n,medjutim jednom je n parno drugi put neparno nije jasno dokle ide sumiranje.
[ petarm @ 22.07.2008. 19:53 ] @
[ h4su @ 22.07.2008. 20:49 ] @
[ petarm @ 22.07.2008. 20:53 ] @
Pa nije isto, al ista je forma resenja! Ja kad resavam problem koji sam zadao, videces ako ga pazljivo procitas, ne znam dal je n parno ili neparno? Pa pretpostavim i jedan i drugi slucaj i ocigledno dobijem sta dobijem!
[ h4su @ 23.07.2008. 00:28 ] @
Pusti to haj rjesi onaj integral :D
[ Aleksandar Đokić @ 23.07.2008. 03:40 ] @
a pa cim je 76' 100% cu probati da resim...jaoo boze
[ Nedeljko @ 23.07.2008. 08:21 ] @
Citat: petarm: Mene zapravo zanima da li ja mogu da kad izracunam jednu od ovih suma npr.  da tvrdim da za ovu drugu sumu dobijam isti rezultat da tvrdim da za ovu drugu sumu dobijam isti rezultat  bez izracunavanja? I ima li neke veze sa kombinatorikom sto se dobija bas bez izracunavanja? I ima li neke veze sa kombinatorikom sto se dobija bas 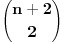 ? ?Ako je  neparno, na primer neparno, na primer  za neko celo za neko celo 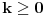 , onda je , onda je 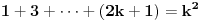 , odnosno , odnosno  i nikako ne moze biti ono sto si dobio. Recimo, za i nikako ne moze biti ono sto si dobio. Recimo, za 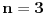 je je 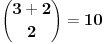 odnosno odnosno  . .[ Nedeljko @ 23.07.2008. 08:23 ] @
[ igorpet @ 23.07.2008. 11:43 ] @
Citat: h4su: Pusti to haj rjesi onaj integral :D 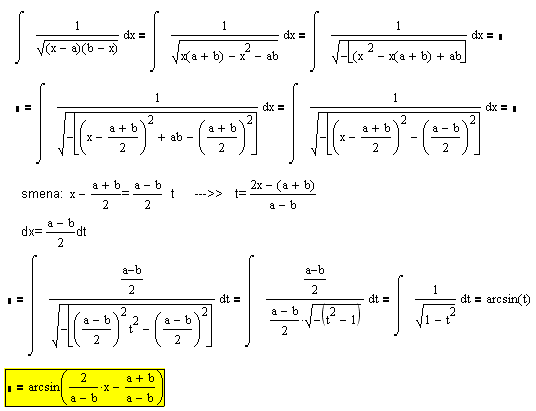 Pa smena i nije nesto mnogo interesantna. Nadam se da resenje zadovoljava. Ili ima neki interesantniji nacin za resavanje? [ Nedeljko @ 23.07.2008. 14:22 ] @
[ igorpet @ 23.07.2008. 16:15 ] @
Citat: Prva smena dovodi do kompleksnog resenje (a zatim treba naci i t i sve to malo srediti), ali kako u drugoj dobijas samo cos(t)^2 ??? Da li ja negde gresim ili si ti Nedeljko negde napravio previd? 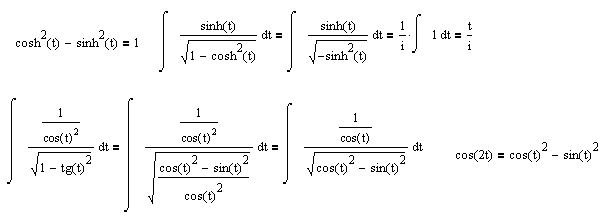 [ petarm @ 23.07.2008. 18:55 ] @
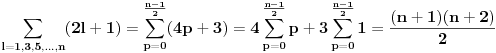 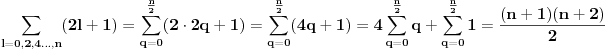 Nadam se da je sad ovo zapisano u korektnom obliku? Ja znam da mi je 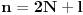 Ja treba da izracunam sledece 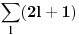 Zbog veze izmedju  i i  ja mogu da imam jednu od gornje 2 sume! Jel tako? Da li ja mogu da PP da je ja mogu da imam jednu od gornje 2 sume! Jel tako? Da li ja mogu da PP da je neparno npr. i da prosumiram prvu od gornje dve sume i da napisem neparno npr. i da prosumiram prvu od gornje dve sume i da napisem 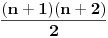 i kazem to mi je rezultat u zavisnosti od i kazem to mi je rezultat u zavisnosti od  , a drugu sumu ne moram sumirati jer znam da cu dobiti , a drugu sumu ne moram sumirati jer znam da cu dobiti 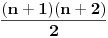 zbog...? zbog...?[ h4su @ 23.07.2008. 21:12 ] @
Citat: Nedeljko: Pretpostavicu da je 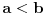 Drugi slucaj je analogan. Drugi slucaj je analogan.Jedan od nacina je Ojlerova smena  , , 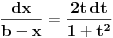 , kada se integral svodi na , kada se integral svodi na 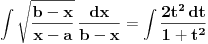 i ne vidim nikakvu pamet u tome. Ovo je potpuno tipski zadatak i ovo je standardno resenje, kao i ono koje je igorpet napisao. i ne vidim nikakvu pamet u tome. Ovo je potpuno tipski zadatak i ovo je standardno resenje, kao i ono koje je igorpet napisao.Meni je ova smjena interesantna x=acos2t+bsin2t 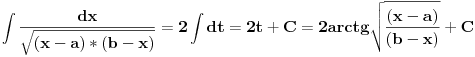 Tema je zanimljivi zadaci eleg rjesenja,meni je ovo rjesenje interesantno,nisam ni rekao da je nesto tezak zadatak.Evo jedan tezak zadatak (bar meni) koji sam vec ranije postavio i niko se nije javio. Konstruisati kružmicu kojoj je centar na datoj pravi a iz date dvije tacke križnica se vidi pod datim uglovima. [ Nedeljko @ 23.07.2008. 21:32 ] @
Citat: igorpet: Da li ja negde gresim ili si ti Nedeljko negde napravio previd? Nedeljko je napravio previd znaka minus pod korenom. Neka su 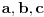 realni brojevi, pri čemu je realni brojevi, pri čemu je 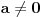 . Da bi podintegralna funkcija u kojoj se pojavljuje . Da bi podintegralna funkcija u kojoj se pojavljuje 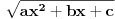 bila definisana na bar jednom intervalu, funkcija bila definisana na bar jednom intervalu, funkcija 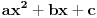 mora imati pozitivnu vrednost u bar jednoj tački, koju ćemo označiti sa mora imati pozitivnu vrednost u bar jednoj tački, koju ćemo označiti sa  . Nadalje će . Nadalje će  biti racionalna funkcija dve promenljive sa realnim koeficijentima, koja je definisana u bar jednoj tački realne ravni. biti racionalna funkcija dve promenljive sa realnim koeficijentima, koja je definisana u bar jednoj tački realne ravni.Razmotrimo problem svođenja integrala 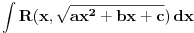 na integral racionalne funkcije. na integral racionalne funkcije.Ako je 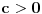 , onda se može koristiti druga Ojlerova smena: , onda se može koristiti druga Ojlerova smena: 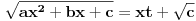 , , 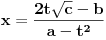 , , 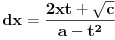 . Pomenuću i da je druga Ojlerova smena dovoljna za svođenje svakog integrala ovakvog tipa (bez obzira na znak broja . Pomenuću i da je druga Ojlerova smena dovoljna za svođenje svakog integrala ovakvog tipa (bez obzira na znak broja  ) na integral racionalne funkcije, jer se nakon smene ) na integral racionalne funkcije, jer se nakon smene 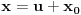 dobija integral na koji se može primeniti druga Ojlerova smena. dobija integral na koji se može primeniti druga Ojlerova smena.Ako je  , onda se može koristiti prva Ojlerova smena , onda se može koristiti prva Ojlerova smena 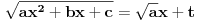 , , 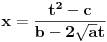 , , 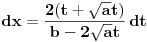 . .Ako je 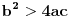 , to jest polinom , to jest polinom 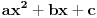 ima dve realne nule, koje ćemo označiti sa ima dve realne nule, koje ćemo označiti sa 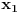 i i 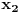 , recimo , recimo  , onda se može koristiti treća Ojlerova smena , onda se može koristiti treća Ojlerova smena 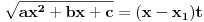 , , 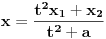 , , 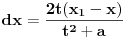 . .U svakom slučaju, iracionalnost 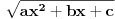 se uvek može linearnom smenom svesti na tačno jedan od sledeća tri oblika: se uvek može linearnom smenom svesti na tačno jedan od sledeća tri oblika: 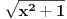 , , 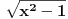 i i 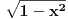 . U prvom slučaju se mogu koristiti smene . U prvom slučaju se mogu koristiti smene 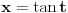 , , 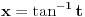 i i 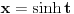 . U drugom slučaju se mogu koristiti smene . U drugom slučaju se mogu koristiti smene 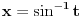 , , 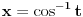 i i 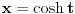 . U trećem slučaju se mogu koristiti smene . U trećem slučaju se mogu koristiti smene 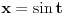 , , 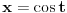 . Na taj način se dobijaju integrali koji se standardnim smenama svode na integrale racionalnih funkcija. . Na taj način se dobijaju integrali koji se standardnim smenama svode na integrale racionalnih funkcija.[ igorpet @ 23.07.2008. 22:23 ] @
Citat: h4su: Meni je ova smjena interesantna x=acos2t+bsin2t Smena jeste interesantna i prilicno je neocigledna, a ima i da se radi dok se ne uprosti. Interesantnije bi bilo da je to jedina moguca smena, ovako kada moze mnogo jednostavnije gubi se poenta, ali je ipak OK. Nedeljko, bas si se iskupio za onaj minus Ja za Ojlerovim smenata potezem samo kada ne moze drugacije, a ovde je bilo dovoljno kvadratni trinom dovesti na kanonicni oblik i primeniti klasicnu i logicnu smenu. [ Nedeljko @ 24.07.2008. 11:09 ] @
Citat: h4su: Meni je ova smjena interesantna x=acos2t+bsin2t. Jos "interesantnija" je smena 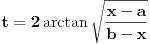 , kojom se integral svodi na , kojom se integral svodi na 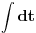 . Tako mozes jednom smenom "resiti" bilo koji integral kada znas resenje. . Tako mozes jednom smenom "resiti" bilo koji integral kada znas resenje.[ igorpet @ 24.07.2008. 13:00 ] @
Citat: Nedeljko: Jos "interesantnija" je smena 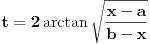 , kojom se integral svodi na , kojom se integral svodi na 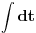 . Tako mozes jednom smenom "resiti" bilo koji integral kada znas resenje. . Tako mozes jednom smenom "resiti" bilo koji integral kada znas resenje.Pa Nedeljko x=acos2t+bsin2t je u stvari 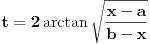 To je ista ta smena U stvari x=acos2t+bsin2t je 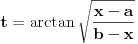 i samo je pitanje da li ce integral biti i samo je pitanje da li ce integral biti 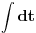 ili ili 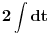 [Ovu poruku je menjao igorpet dana 24.07.2008. u 14:16 GMT+1] [ h4su @ 24.07.2008. 14:04 ] @
Nedeljko ne znam sto si se uhvatio te smjene toliko,jel ti nesto narocito smeta ili sta.Nekome co ovo sto si napisao koristiti i to je to.Drugi zadatak je "interesantniji" kad ste se uhvatili toga a za njega ne znam rjesenje pa ne znam ni "smjenu".
[ igorpet @ 24.07.2008. 14:38 ] @
Citat: h4su: Drugi zadatak je "interesantniji" ... ne znam rjesenje pa ne znam ni "smjenu". Citat: Konstruisati kružmicu kojoj je centar na datoj pravi a iz date dvije tacke križnica se vidi pod datim uglovima. Cudan neki integral, ... sa kružmicom Mora i da je neka jako interesantna smena. Da znam resenje sigurno bih ga napisao, a ovako malo me mrzi da se udubljujem u problem, pa sam siguran da ce to neko ko zna iz prve [ Nedeljko @ 24.07.2008. 15:50 ] @
@h4su
Ma, ne smeta mi nista, samo sam hteo da pokazem kako "moc smene" moze da zavara. [ Nedeljko @ 31.07.2008. 12:33 ] @
[ petarm @ 01.08.2008. 18:00 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|