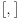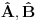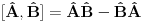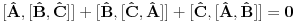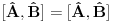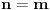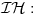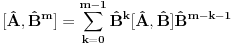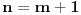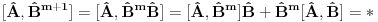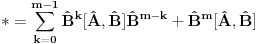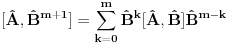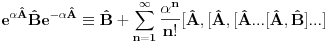[ petarm @ 20.07.2008. 23:26 ] @
|
[ petarm @ 22.07.2008. 20:36 ] @
Da dokazem ove osobine:
1.) 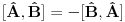 dokaz 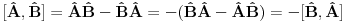 2.) 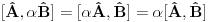 dokaz Odavde se jasno moze videti bilinearnost komutatora! dokaz 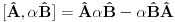  je broj pa komutira sa ovim operatorima! Odakle sledi gornji rezultat! je broj pa komutira sa ovim operatorima! Odakle sledi gornji rezultat! 3.) 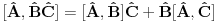 dokaz 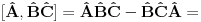  I zdruzivanjem dobijamo gornji rezultat! 4.) 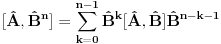 dokaz Dokazuje se matematickom indukcijom. Dokazao sam je u okviru ove teme http://www.elitesecurity.org/t...ljivi-zadaci-elegantna-resenja Ko uspe da dokaze na neki drugi nacin bez indukcije nek okaci! [ petarm @ 26.07.2008. 00:42 ] @
[ petarm @ 29.07.2008. 16:49 ] @
ZADATAK
Neka su 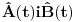 operatori fizickih velicina sistema koji se opisuje Hamiltonijanom operatori fizickih velicina sistema koji se opisuje Hamiltonijanom 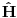 . Pokazati da tada vazi relacija: . Pokazati da tada vazi relacija: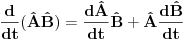 RESENJE: Mislim da je najkorektnije resenje primenom Hajzenbergovih jednacina kretanja 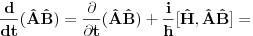 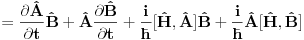 I odavde se lako dobija trazena relacija! Resenje koje se uglavnom daje po zbirkama polazi od sledeceg 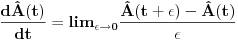 U kom slucaju za operatore uopste vazi ova relacija? Primenom ove definicije relativno se lako dobija 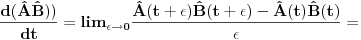 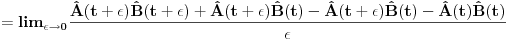 Odakle se lako dobija trazena relacija! U kojim slucajevima se definicija izvoda fja moze primenjivati na operatore? [ petarm @ 02.08.2008. 01:32 ] @
Evo sad jednog lepog zadatka!
ZAD Neka je 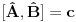 . Pokazati da vazi . Pokazati da vazi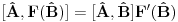 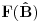 -proizvoljna diferencijabilna funkcija -proizvoljna diferencijabilna funkcija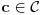 RESENJE: Dacu odmah ovde i resenje zadatka! Nadam se da ce ova tema u buducnosti biti od koristi ljudima koji spremaju kvantnu 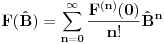 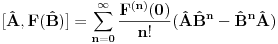 E sad dolazim do necega sto je vec pokazano u ovoj temi 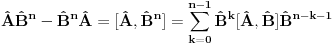 Ali kako 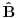 komutira sa komutira sa 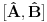 dobijamo dobijamo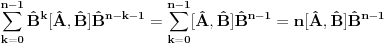 Pa je 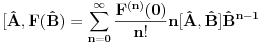 Uvede se smena 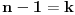 i lako se dobija trazeni rezultat! i lako se dobija trazeni rezultat!Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|