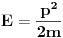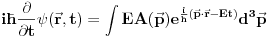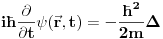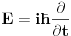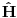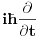[ petarm @ 26.07.2008. 02:55 ] @
Sredingerova jednacina mora biti linearna zbog principa superpozicije! Ovo je skroz jasno! Medjutim negde sam nasao mora biti linearna i homogena zbog principa superpozicije? Zasto homogena?

Formalno izvodjenje kakvo samo radili na predavanjima je sledece! Rekli smo svaka cestica ima i talasna svojstva.

monohromatski talas -

I onda smo fju stanja trazili u vidu superpozicije monohromatskih talasa


Zasto amplituda u opstem slucaju zavisi od impulsa?

- nerelativisticki slucaj

Zatim se dobija





I odatle imamo




Ovo je za slucaj slobodne cestice!

U opstem slucaju imamo



Koliko je ovo formalno izvodjenje korektno? Kazem formalno jer ipak je SJ postulat!

U kom slucaju ja mogu reci

?

I kad mogu pricati o jednakosti operatora i ?




[ kajla @ 26.07.2008. 17:08 ] @
Citat:
petarm: Sredingerova jednacina mora biti linearna zbog principa superpozicije! Ovo je skroz jasno! Medjutim negde sam nasao mora biti linearna i homogena zbog principa superpozicije? Zasto homogena?

Formalno izvodjenje kakvo samo radili na predavanjima je sledece! Rekli smo svaka cestica ima i talasna svojstva.

monohromatski talas -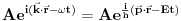

I onda smo fju stanja trazili u vidu superpozicije monohromatskih talasa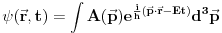


Zasto amplituda u opstem slucaju zavisi od impulsa?

Mislim ti si ovim fakticki predpostavio da je evolucija svojstvenog stanja data sa exp(-i/h Et), sto je ekvivalentno sa sj. Ovo se vise moze svatiti kao neki pokaz ne kao dokaz. (mada se meni vise svidja da se uspostavi veza izmedju sj. i hamiltoj jakobijeve jednacine, pogledaj [Landau])
Citat:

- nerelativisticki slucaj

Zatim se dobija





I odatle imamo




Ovo je za slucaj slobodne cestice!

U opstem slucaju imamo



Koliko je ovo formalno izvodjenje korektno? Kazem formalno jer ipak je SJ postulat!

U kom slucaju ja mogu reci

?

I kad mogu pricati o jednakosti operatora i ?

Izjadnacavati broj i operator ima samo neko neformalno znacenje (tj. da isto deluju na svojstveni vektor). Sj. ti je ustvari iskaz da evoluciju talasne fje diktira hamiltonijan sistema. (matematicki operatori H i d/dt nisu uopste isti samo isto deluju na talasne funkcije sistema ciji je hamiltonijan H, na neku proizvoljnu fju naravno ne deluju na isti nacin)

pozdav.
[ tomkeus @ 27.07.2008. 10:59 ] @
Citat:
petarm: 

Zasto amplituda u opstem slucaju zavisi od impulsa?


Pa pogledaj, ako ti je partikularno rešenje u trenutku t dato sa 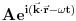onda ćeš opšte rešenje u trenutku t dobiti sumiranjem svih partikularnih rešenja u trenutku t. Partikularna rešenja u trenutku t prebrojava parametar p, tj. impuls tako da se opšte rešenje dobija sumiranjem po impulsu što znači da, barem što se sumiranja tiče .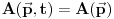

Citat:
petarm:I kad mogu pricati o jednakosti operatora i ?


To možeš da kažeš u nerelativističkom slučaju.

[Ovu poruku je menjao tomkeus dana 27.07.2008. u 12:50 GMT+1]
[ petarm @ 28.07.2008. 17:20 ] @
Citat:
kajla: Ovo se vise moze svatiti kao neki pokaz ne kao dokaz.

A sta je tacno pokaz?
[ kajla @ 28.07.2008. 19:44 ] @
Pa kad nesto nije strog dokaz (mada vecina dokaza u fiziki nije stoga) vec cisto ti pokazuje kako da dodjes do nekog rezultata...

pozdrav.
[ petarm @ 29.07.2008. 13:57 ] @
Citat:
tomkeus: To možeš da kažeš u nerelativističkom slučaju.

[Ovu poruku je menjao tomkeus dana 27.07.2008. u 12:50 GMT+1]


A moze li se reci da su jednaki operator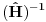i i 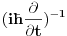u nerelativistickom slucaju!