Da.

Da to sam i ja mislio! I jeste mi logicno. Ali skoro sam pricao sa jednim matematicarem iz Zagreba koji mi je rekao da ovo nije tako u opstem slucaju! Bilo je neke price sa razapinjanjem prostora i sl.

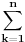
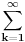
Naime on je rekao da u slucaju baze se svaki vektor iz prostora moze izraziti putem konacne linearne kombinacije baznih vektora dok je kod ortonormirane baze moguc slucaj ? Meni ovo zvuci prilicno nelogicno ali sam zeleo da se konsultujem sa nekim od vas matematicara!

Doduse meni ovo najvise smrdi zbog Gram-Smitovog postupka! Voleo bih ipak komentar!

Ovde je važno znati da li se radi o algebarskoj (Hamelovoj) ili ortogonalnoj bazi. Osim linearne nezavisnosti, od algebarske baze se još traži da joj linearni omotač bude jednak celom prostoru, a od ortogonalne da joj vektori budu uzajamno ortogonalni i da joj linearni omotač bude svuda gust podskup celog prostora. Tako razlikujemo algebarsku i ortogonalnu dimenziju Hilbertovog prostora. Ako je ortogonalna dimenzija jednaka onda je algebarska dimenzija jednaka .

U fizici se dosta radi sa projektorima koji projektuju na svojstveni pravac . U funkcionalnim analizama vidjao sam da ove operatore nazivaju ortogonalni projektori! Ima li ovo Nedeljko veze sa ovim sto si napisao?

Ako je ortogonalna normirana baza Hilbertovog prostora i i ortogonalni projektor na potprostor . Tada se vektor projektuje na vektor .