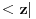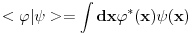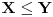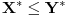[ petarm @ 18.08.2008. 02:10 ] @
|
[ petarm @ 18.08.2008. 02:28 ] @
[ Nedeljko @ 18.08.2008. 20:29 ] @
Mislim da bi trebao da promeniš pristup učenju matematičkih aparata.
[ petarm @ 18.08.2008. 21:00 ] @
Lako je to reci! Zapravo je prilicno tesko! Matematicari i fizicari razlicito tretiraju matematiku! Kod oscilovanja zice matematicar ispituje egzistenciju resenja, fizicar uzme zatrese zicu vidi da osciluje i kaze resenje postoji ajd da resim jednacinu! Oznake su najcesce skroz drugacije i nemam vremena da maltene nijednu matematicku knjigu citam od pocetka do kraja vec gledam delove koji su mi potrebni u datom trenutku! A u svakoj teoremi vidim pozivanje na 10 prethodnih pa ih onda najcesce ne ucim!
[ Nedeljko @ 19.08.2008. 10:54 ] @
Bez muke nema nauke. Čime se baviš? Jesi li student?
[ petarm @ 19.08.2008. 11:03 ] @
Da! Treba da upisem cetvrtu godinu! Ako uspem da se uklopim ici cu da slusam Funkcionalnu analizu s matematicarima u sledecoj skolskoj godini!
Zamolio bih te ako mozes bar delimicno da odgovoris na moje pitanje od gore! Unapred hvala! [ Nedeljko @ 19.08.2008. 11:49 ] @
Nisam previše upućen u formalizam koji koriste fizičari, ali ću pokušati da odgovorim onako kako sam ja razumeo stvari koje si napisao.
Dualni vektor Banahovog prostora  je ništa drugo do ograničen antilinearan funkcional tog Banahovog prostora. Ako ga označiš sa je ništa drugo do ograničen antilinearan funkcional tog Banahovog prostora. Ako ga označiš sa 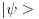 (ili (ili 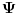 ), onda je ), onda je 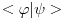 vrednost tog funkcionala u tački vrednost tog funkcionala u tački  (odnosno (odnosno 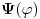 ). ).E, sad, postoje teoreme o reprezentaciji dualnih vektora. Ako su 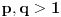 takvi da je takvi da je 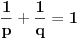 onda: onda:1. Za svaki dualni vektor 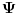 prostora prostora 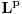 postoji tačno jedan vektor postoji tačno jedan vektor 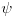 prostora prostora 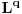 takav da je takav da je 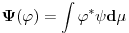 za svako za svako 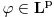 i pritom je i pritom je 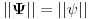 . .2. Za ma koji vektor 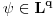 je sa je sa 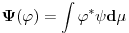 dobro definisan jedan dualni vektor prostora dobro definisan jedan dualni vektor prostora 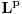 . .3. Ako se zbir duala definiše kao zbir funkcija, a množenje skalarom kao proizvod konjugata tog skalara i preslikavanja, onda je preslikavanje 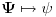 linearno i bijektivno. linearno i bijektivno.Iz ovih razloga se 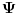 i i 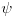 identifikuju. identifikuju.[ petarm @ 19.08.2008. 12:23 ] @
Hvala na odgovoru!
Citat: Nedeljko: Dualni vektor Banahovog prostora  je ništa drugo do ograničen antilinearan funkcional tog Banahovog prostora. Ako ga označiš sa je ništa drugo do ograničen antilinearan funkcional tog Banahovog prostora. Ako ga označiš sa 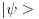 (ili (ili 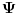 ), onda je ), onda je 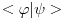 vrednost tog funkcionala u tački vrednost tog funkcionala u tački  (odnosno (odnosno 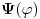 ). ).Ovde mislim da se nismo razumeli! Sta si ti oznacio sa 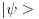 ? ? 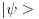 je vektor iz Banahovog prostora, a je vektor iz Banahovog prostora, a 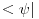 iz njemu dualnog prostora! Oznaka iz njemu dualnog prostora! Oznaka 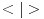 nije isto sto i nije isto sto i 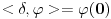 ? ?Citat: Nedeljko: E, sad, postoje teoreme o reprezentaciji dualnih vektora. Ako su 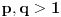 takvi da je takvi da je 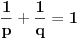 onda: onda:1. Za svaki dualni vektor 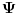 prostora prostora 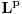 postoji tačno jedan vektor postoji tačno jedan vektor 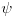 prostora prostora 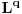 takav da je takav da je 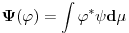 za svako za svako 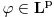 i pritom je i pritom je 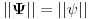 . .2. Za ma koji vektor 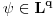 je sa je sa 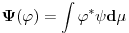 dobro definisan jedan dualni vektor prostora dobro definisan jedan dualni vektor prostora 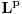 . .3. Ako se zbir duala definiše kao zbir funkcija, a množenje skalarom kao proizvod konjugata tog skalara i preslikavanja, onda je preslikavanje 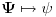 linearno i bijektivno. linearno i bijektivno.Iz ovih razloga se 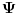 i i 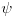 identifikuju. identifikuju.Ovo sam video mada me je zbunilo jer sam nasao na jednom mestu 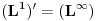 . . 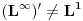 ? ?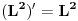 Kako bi ti prostim recimo objasnio koja je razlika izmedju  i njegovog duala? i njegovog duala? I zasto je 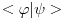 skalarni proizvod za skalarni proizvod za 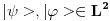 ? ?[ Mlatko @ 19.08.2008. 14:30 ] @
Citat: Da se ukljucim - vec od jucer ti zelim odgovoriti, ali me u potpunom objasnjenju zeza jedna stvar koju nikako da sebi objasnim pa sve odgadjam da napisem. Ali evo bar nesto, jer vidim da te muci. Tebe najvise zeza to sto ti se sva prica oko duala svodi na kompleksnu konjugaciju. Ovo bi ti trebalo pomoci: dualni prostor nekog prostora E je prostor svih funkcionala koji djeluju na njemu. Detaljnije: Neka imamo prostor svih ketova, nazovimo ga E. Polje pridruzeno tom prostoru u kvantnoj je C (kompleksni brojevi). Svaki operator f:E->C zovemo funkcional (dakle vrijednosti su mu kompleksni brojevi) I sad imamo - dualni prostor prostora E je prostor svih funkcionala koji djeluju na E. Znaci, dualni prostor prostora  je jednostavno skup svih funkcionala koji djeluju na njemu, a kakve to ima veze s kompleksnom konjugacijom na koju si navikao bit ce jasno nadam se do kraja :) je jednostavno skup svih funkcionala koji djeluju na njemu, a kakve to ima veze s kompleksnom konjugacijom na koju si navikao bit ce jasno nadam se do kraja :)To je oznaka za skalarni proizvod u diracovoj notaciji. Dakle 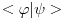 je isto sto i ( je isto sto i ( ) (skalarni produkt dvaju ketova). ) (skalarni produkt dvaju ketova).E sad kako odjednom ket postao bra? Zato sto svakom ketu 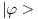 iz L^2 mozemo pridruziti funkcional (bra) iz L^2 mozemo pridruziti funkcional (bra) 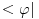 iz dualnog prostora od L^2 na sljedeci nacin: iz dualnog prostora od L^2 na sljedeci nacin: neka rezultat djelovanja tog funkcionala 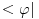 na bilo koji na bilo koji 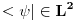 bude nista drugo nego skalarni produkt bude nista drugo nego skalarni produkt 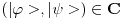 . .Znaci 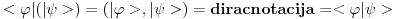 E sad kako je ovo pridruzivanje ketova braovima antilinearno, to 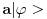 pridruzujemo pridruzujemo 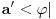 (sa a' sam oznacio konjugirani a iz C) (sa a' sam oznacio konjugirani a iz C)Zato se braovi (elementi dualnog prostora) tehnicki nalaze tako da jednostavno konjugiramo ket koji smo mu pridruzili. U matricnoj notaciji, gdje ketove reprezentiramo matricama-colonama, jos trebamo pridruzeni bra transponirati, da bismo ih uopce mogli matricno pomnoziti (jer produkt dviju matrica-kolona nije definiran). .............. Ono sto si jos u prvom postu pitao zasto je, ako uzimamo podskupove prostora, njihov odgovarajuci dual "veci", cu pokusati otipkati kasnije, naravno ako te to jos uvijek zanima :) [ Nedeljko @ 19.08.2008. 16:18 ] @
@Zbunilo me je to sto si napisao da je
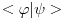 antiilinearan po prvom argumentu, a linearan po prvom, pa sam mislio da fizicarima dualni vektori odgovaraju antilinearnim funkcionalima, a ne linearnim kao u matematici. No, posle tvog poslednjeg posta su mi stvari jasnbije.. antiilinearan po prvom argumentu, a linearan po prvom, pa sam mislio da fizicarima dualni vektori odgovaraju antilinearnim funkcionalima, a ne linearnim kao u matematici. No, posle tvog poslednjeg posta su mi stvari jasnbije..Znaci, bra vektor 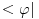 Banahovog prostora Banahovog prostora  je pridruzivanje svakom ketu, tj. vektoru je pridruzivanje svakom ketu, tj. vektoru 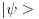 po tacno jednog skalara u oznaci po tacno jednog skalara u oznaci 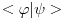 tako da vazi: tako da vazi:1. 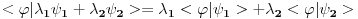 (linearnost), (linearnost),2. 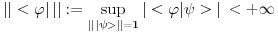 (ogranicenost). (ogranicenost).Zbir dualnih vektora 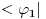 i i 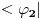 definisemo kao dualni vektor u oznaci definisemo kao dualni vektor u oznaci 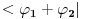 definisan sa definisan sa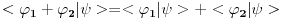 Pritom je 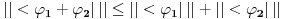 . Proizvod skalara . Proizvod skalara  i dualnog vektora i dualnog vektora 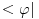 u oznaci u oznaci 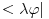 definise se sa definise se sa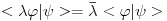 . .E, sad se vrati na teoreme o reprezentaciji ogranicenog linearnog funkcionala (ili dualnog vektora), pa pitaj sta ti ne bude jasno. [ petarm @ 19.08.2008. 16:57 ] @
@Mlatko
Pozdrav pre svega! Mene zapravo najvise zanima zasto je to skalarni proizvod bas za 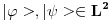 ? ?@Mlatko dualni prostor nekog prostora E je prostor svih funkcionala koji djeluju na njemu. Ovde je meni problematicno zato sto je taj skup funkcionala bas 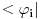 a to su neki vektori iz dualnog prostora! Ako posmatram samo jedan taj bra kako ja da zakljucim tu pricu o funkcionalima! a to su neki vektori iz dualnog prostora! Ako posmatram samo jedan taj bra kako ja da zakljucim tu pricu o funkcionalima!Jer zapravo u  imamo sledecu pricu imamo sledecu pricu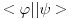 = dejstvo funkcionala na = dejstvo funkcionala na 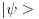 a ovo je bas skalarni proizvod u slucaju a ovo je bas skalarni proizvod u slucaju 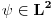 @Mlatko Ono sto si jos u prvom postu pitao zasto je, ako uzimamo podskupove prostora, njihov odgovarajuci dual "veci", cu pokusati otipkati kasnije, naravno ako te to jos uvijek zanima Da zanima me prica! Video sam primere kako ti suzavanjem nekog prostora i odlazeci u dual tog manjeg prostora mozes dobiti svoju vrednost u nuli, ali zanima me sustinski zasto! [ Nedeljko @ 19.08.2008. 19:53 ] @
Citat: Mlatko: I sad imamo - dualni prostor prostora E je prostor svih funkcionala koji djeluju na E. Linearnih i ograničenih funkcionala. @petarm Ako dozvoliš, mogao bih na ponešto da odgovorim. Neka 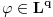 . Funkcional . Funkcional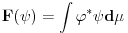 na prostoru 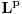 je dobro defionisan, linearan i ograničen (pri čemu je je dobro defionisan, linearan i ograničen (pri čemu je 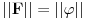 ). Za različite ). Za različite 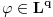 se uvek dobijaju različiti funkcionali i svaki linearni ograničeni funkcional je tog oblika (za neko se uvek dobijaju različiti funkcionali i svaki linearni ograničeni funkcional je tog oblika (za neko 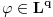 ). Zbog toga se umesto ). Zbog toga se umesto  piše piše 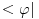 , a umesto , a umesto 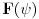 se piše se piše 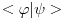 . E, sad, po analogiji fizičari vole da umesto . E, sad, po analogiji fizičari vole da umesto 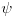 pišu pišu 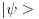 . U svakom slučaju, iz ovih definicija se dobija da je . U svakom slučaju, iz ovih definicija se dobija da je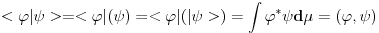 . .Naravno, ovo poslednje za 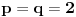 . Da li sada razlikuješ teoreme od definicija i da li je ovo bar malo pomoglo? . Da li sada razlikuješ teoreme od definicija i da li je ovo bar malo pomoglo?Citat: petarm: Ono sto si jos u prvom postu pitao zasto je, ako uzimamo podskupove prostora, njihov odgovarajuci dual "veci", cu pokusati otipkati kasnije, naravno ako te to jos uvijek zanima :) Ma da nisu u pitanju količnički prostori i njihovi duali? [ petarm @ 19.08.2008. 23:07 ] @
Ovo je dosta pomoglo! Hvala puno!
Citat: Nedeljko: Ma da nisu u pitanju količnički prostori i njihovi duali? Ne zapravo sam mislio na sledecu stvar! Ti imas korespodenciju kad radis u  da imas braova da imas braova 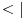 kolko imas i ketova kolko imas i ketova 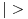 . . Posmatrajmo na primer Svarcov prostor 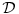 . O njemu smo vec diskutovali! . O njemu smo vec diskutovali! 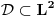 . A vazi . A vazi 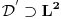 . Da li se moze ovo nekako intuitivno zakljuciti? I da li ovo mogu posmatrati kao slucaj imam vise braova . Da li se moze ovo nekako intuitivno zakljuciti? I da li ovo mogu posmatrati kao slucaj imam vise braova 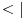 nego ketova nego ketova 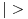 ? E sad nisam bas siguran kako ti definises kolicnicki prostor?! ? E sad nisam bas siguran kako ti definises kolicnicki prostor?! [ petarm @ 19.08.2008. 23:11 ] @
Ja to ovako zamisljam!
[ Nedeljko @ 20.08.2008. 09:34 ] @
Sa Švarcovim prostorom budi oprezan. Jeste
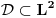 , ali da bi to bio potprostor, mora mu nasleđivati strukturu. OK, on jeste njegov vektorski potprostor, ali u definiciji (neprekidnog) duala figuriše i norma. Švarcov prostor nije normirani prostor. Priseti se kako je uvedena konvergencija u njemu. Lakše je zadovoljiti uslov neprekidnosti pod jačim pretpostavkama. Zato je , ali da bi to bio potprostor, mora mu nasleđivati strukturu. OK, on jeste njegov vektorski potprostor, ali u definiciji (neprekidnog) duala figuriše i norma. Švarcov prostor nije normirani prostor. Priseti se kako je uvedena konvergencija u njemu. Lakše je zadovoljiti uslov neprekidnosti pod jačim pretpostavkama. Zato je 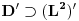 . .[ petarm @ 20.08.2008. 13:15 ] @
[ Nedeljko @ 20.08.2008. 19:08 ] @
Citat: petarm: Da li ovo vazi 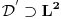 ? ?Da, ali 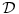 nije Banahov pristor jer nemaš normu. nije Banahov pristor jer nemaš normu.Citat: Ovo važi za Banahove prostore. Zato je u matišu vrlo bitan kontekst tvrđenja i zato sam ti rekao da promeniš pristup učenju matiša. Ako nemaš vremena, slobodno preskoči sve dokaze i sva izvođenja. Sve ostalo ti je važno. [ petarm @ 20.08.2008. 19:28 ] @
Citat: Nedeljko: Ovo važi za Banahove prostore. Zato je u matišu vrlo bitan kontekst tvrđenja i zato sam ti rekao da promeniš pristup učenju matiša. Ako nemaš vremena, slobodno preskoči sve dokaze i sva izvođenja. Sve ostalo ti je važno. Hvala na savetu! Mozes li mi odgovoriti zasto kada radim dual od 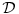 dobijam veci prostor, a to isto ne vazi za Banahove prostore?! dobijam veci prostor, a to isto ne vazi za Banahove prostore?![ Nedeljko @ 20.08.2008. 20:20 ] @
Ako bi u Švarcovom prostoru uveo integralnu normu, nizovi funkcija bi mnogo češće konvergirali, pa bi bilo više pojedinačnih slučajeva kada linearni funkcional treba da konvergira, odnosno teže bi se dobijali neprekidni funkcionali. Ako pređeš na potprostor ne menjajući konvergenciju, onda taj faktor nemaš, već imaš manje stepeni slobode pri izboru funkcionala (funkcionali na celom prostoru se mogu razlikovati, ali da se podudaraju na potprostoru).
[ petarm @ 21.08.2008. 23:24 ] @
Ponekad ljudi ne pisu
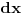 kod integracije! Odnosno pisu npr. kod integracije! Odnosno pisu npr. 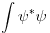 Da li je ovo korektno? Inace u fizici kada napises 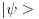 mislis na apstraktni vektor za koji ti nije bitna reprezentacija. A kad ti treba reprezentacija koristis sledece mislis na apstraktni vektor za koji ti nije bitna reprezentacija. A kad ti treba reprezentacija koristis sledece 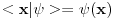 - koordinatna reprezentacija, - koordinatna reprezentacija, 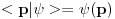 - impulsna reprezentacija... - impulsna reprezentacija...Ti si napisao 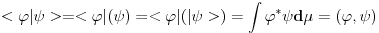 A to je skroz u skladu sa ovim sto sam malopre napisao! 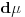 ti je mera cega? ti je mera cega?[ Nedeljko @ 22.08.2008. 12:29 ] @
Citat: petarm: 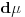 ti je mera cega? ti je mera cega?To je oynaka mere po kojoj se vrši integracija - u ovom slučaju se misli na Lebegovu meru na skupu realnih brojeva. Obnovi definiciju Lebegovog integrala. Citat: Da ako se zna na koju se meru misli. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|