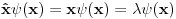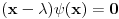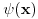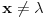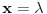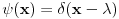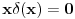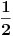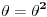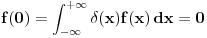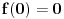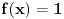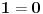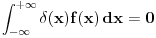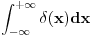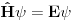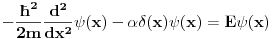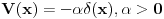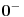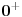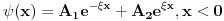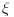[ petarm @ 20.08.2008. 19:39 ] @
|
[ Nedeljko @ 20.08.2008. 20:09 ] @
Proizvoljna distribucija se može množiti beskonačno diferencijabilnom funkcijom i slagati (sa bilo koje strane) sa linearnom funkcijom. O tome je već bilo reči.
[ petarm @ 20.08.2008. 20:16 ] @
Ono sto sam hteo da istaknem ovde je da se prilikom resavanja svojstvenog problema dobija svojstvena funkcija koja nije funkcija?!
[ Nedeljko @ 20.08.2008. 20:24 ] @
[ petarm @ 21.08.2008. 00:27 ] @
Na slici 1. pokazao sam ideju zbog koje se uzima da je
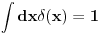 . Uzeo sam pravougaonik dimenzija . Uzeo sam pravougaonik dimenzija 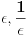 . Povrsina ovog pravougaonika je . Povrsina ovog pravougaonika je  . Kad se pusti da . Kad se pusti da 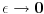 dobija se slika 2. Ovako je ova funkcija originalno definisana od strane Diraka! Zasto je fizicarima u mnogim problemima korisno da se ovako definise! Posmatrajmo npr. sledeci slucaj dobija se slika 2. Ovako je ova funkcija originalno definisana od strane Diraka! Zasto je fizicarima u mnogim problemima korisno da se ovako definise! Posmatrajmo npr. sledeci slucaj 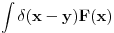 . Fja . Fja  oseca ovaj ako hocete operator jedino u tacki y pa mogu pisati: oseca ovaj ako hocete operator jedino u tacki y pa mogu pisati: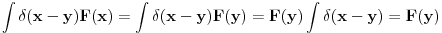 Znam da ovo ne zadovoljava kriterijume matematicara, ali mislim da je tesko naci slucaj gde ovo necu moci da primenim ili nesto da izracunam! A zar nije to na kraju bitno? Mozete reci svoje misljenje o ovome! Citat: Nedeljko: Taj svojstveni problem nema rešenje u prostoru funkcija, ali ima rešenje u prostoru distribucija, kao što jednačina 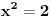 nema rešenja u polju racionalnih, ali ima rešenja u polju realnih brojeva. nema rešenja u polju racionalnih, ali ima rešenja u polju realnih brojeva.Slazem se u potpunosti Nedeljko! Lepo si to uporedio! Mada i 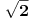 je broj! I ti imas slucaj ovde svaki racionalan broj je realan! Dok ne mozes reci da je svaka fja distribucija! A svuda kada se definise svojstveni problem pod njim se smatra nalazenje svojstvenih vrednosti i funkcija! A Dirakova distribucija nije funkcija! je broj! I ti imas slucaj ovde svaki racionalan broj je realan! Dok ne mozes reci da je svaka fja distribucija! A svuda kada se definise svojstveni problem pod njim se smatra nalazenje svojstvenih vrednosti i funkcija! A Dirakova distribucija nije funkcija! [ Nedeljko @ 21.08.2008. 10:27 ] @
Citat: petarm: Ovako je ova funkcija originalno definisana od strane Diraka! Lebegov integral tako definisane funkcije (eventualno pomnožene nekom funkcijom) je jednak nuli. Ako hoćeš da dobiješ ono što želiš, moraš redefinisati pojam integrala. Jedno od rešenja (mada nije idealno) je teorija distribucija, a drugo je nestdandardna analiza. Citat: petarm: Znam da ovo ne zadovoljava kriterijume matematicara, ali mislim da je tesko naci slucaj gde ovo necu moci da primenim ili nesto da izracunam! A zar nije to na kraju bitno? Pa, bitno je tačno onoliko koliko je bitno da li je taj rezultat tačan. Lično smatram da sve to nema mnogo veze sa napretkom ljudske civilizacije. Živelo bi se i bez matematike i bez kvantne mehanike i sličnu bismo tehnologiju imali. Kojeg god inženjera da sam pitao koliko matematike se koristi u praksi, rekao je nešto poput "zavisi čime se baviš, ja ne koristim ništa". Sve sam skloniji uverenju da je smisao matematike u gnjavaži đaka i studenata i utrkivanju ko je od koga pametniji. [ Nedeljko @ 21.08.2008. 10:32 ] @
Citat: petarm: Dok ne mozes reci da je svaka fja distribucija! Svaka lokalno integrabilna funkcija jeste distribucija. Citat: petarm: A svuda kada se definise svojstveni problem pod njim se smatra nalazenje svojstvenih vrednosti i funkcija! Sopstvenih vrednosti i vektora, pri čemu se mora znati na koji se vektorski prostor to odnosi. [ petarm @ 21.08.2008. 23:35 ] @
Citat: Nedeljko: Pa, bitno je tačno onoliko koliko je bitno da li je taj rezultat tačan. Lično smatram da sve to nema mnogo veze sa napretkom ljudske civilizacije. Živelo bi se i bez matematike i bez kvantne mehanike i sličnu bismo tehnologiju imali. Kojeg god inženjera da sam pitao koliko matematike se koristi u praksi, rekao je nešto poput "zavisi čime se baviš, ja ne koristim ništa". Sve sam skloniji uverenju da je smisao matematike u gnjavaži đaka i studenata i utrkivanju ko je od koga pametniji. S ovim se ne bih slozio u potpunosti! Slazem se da bi se zivelo, ali ne bismo imali istu tehnologiju! Doduse ne znam sta ti tacno smatras pod tehnologijom? Ali i atomska bomba se moze svrstati u to... Nanostrukture su danas u jezivoj ekspanziji, a tu je vrlo cest slucaj da eksperimentalci citiraju teoreticare u svojim istrazivanjima! Ima inzenjera koji koriste mnogo matematike, kao i fizicara! Po meni je problem sto mnogi matematicari gledaju jako usko... To nije formalno dobro-necu dalje da gledam! I vecina matematicara ulazi duboku u formalizam (nemam nista protiv toga ako i dalje mogu da kazu neke stvari na jednostavan nacin!) Citat: Nedeljko: Sopstvenih vrednosti i vektora, pri čemu se mora znati na koji se vektorski prostor to odnosi. Ne razumem zasto si ovde naglasio sopstvenih umesto svojstvenih? I vektora umesto fja? Jer mi smo ovde diskutovali o prostorima fja? Odnosno o beskonacno-dimenzionim prostorima! [ Bojan Basic @ 22.08.2008. 01:20 ] @
Citat: petarm: Po meni je problem sto mnogi matematicari gledaju jako usko... To nije formalno dobro-necu dalje da gledam! Inžinjer može pedeset puta da obavi neke proračune na formalno nekorektan način (recimo, zanemarujući proveru nekih uslova), da dobije pedeset tačnih rezultata (jer su, eto, prilikom tih merenja dotični uslovi bili ispunjeni — iako naš inžinjer to nije znao), ali šta ćemo kad pri pedeset prvom merenju uslovi ne budu ispunjeni i njemu se zgrada sruši jer ih nije proverio? Da li, dakle, govorimo o uskim pogledima matematičarâ, ili ipak o nonšalantnosti inžinjerâ? [ petarm @ 22.08.2008. 08:56 ] @
Nekada je u pitanju i jedno i drugo!
Citat: petarm: Na slici 1. pokazao sam ideju zbog koje se uzima da je 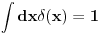 . Uzeo sam pravougaonik dimenzija . Uzeo sam pravougaonik dimenzija 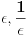 . Povrsina ovog pravougaonika je . Povrsina ovog pravougaonika je  . Kad se pusti da . Kad se pusti da 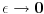 dobija se slika 2. Ovako je ova funkcija originalno definisana od strane Diraka! Zasto je fizicarima u mnogim problemima korisno da se ovako definise! Posmatrajmo npr. sledeci slucaj dobija se slika 2. Ovako je ova funkcija originalno definisana od strane Diraka! Zasto je fizicarima u mnogim problemima korisno da se ovako definise! Posmatrajmo npr. sledeci slucaj 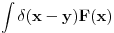 . Fja . Fja  oseca ovaj ako hocete operator jedino u tacki y pa mogu pisati: oseca ovaj ako hocete operator jedino u tacki y pa mogu pisati: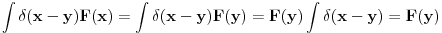 Znam da ovo ne zadovoljava kriterijume matematicara, ali mislim da je tesko naci slucaj gde ovo necu moci da primenim ili nesto da izracunam! A zar nije to na kraju bitno? Mozete reci svoje misljenje o ovome! Iskonstruisi mi pedeset prvo merenje! Nadji mi primer kada ovo nece da radi! Ja tvrdim da ako se ovo bude koristilo zgrada nece pasti! [ Nedeljko @ 22.08.2008. 11:34 ] @
@petarm
Ma imali bismo i televizore i atomske bombe bez neke matematike. Citat: petarm: Iskonstruisi mi pedeset prvo merenje! Nadji mi primer kada ovo nece da radi! Ja tvrdim da ako se ovo bude koristilo zgrada nece pasti! Evo ga: http://www.elitesecurity.org/p1907192 [ petarm @ 22.08.2008. 15:00 ] @
[ petarm @ 22.08.2008. 15:40 ] @
[ Nedeljko @ 22.08.2008. 16:21 ] @
Nauči već jednom definiciju Lebegovog integrala.
[ Nedeljko @ 22.08.2008. 16:58 ] @
A šta te zanima? Integralni račun bez integrala?
[ Nedeljko @ 22.08.2008. 17:03 ] @
[ Nedeljko @ 22.08.2008. 17:05 ] @
[ petarm @ 22.08.2008. 17:13 ] @
Nije!
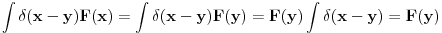 u jednom od postova sam objasnio kako sam dosao do ovog oblika! I sad uzmi da je 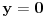 i dobices kao rezultat i dobices kao rezultat 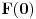 . A ako je ta fja . A ako je ta fja  npr. npr. 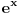 dobices kao rezultat dobices kao rezultat  . Tj. . Tj. 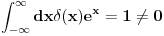 . Ja znam da ti mnogo robujes definicijama i teoremama i svakako jako puno stvari znas! Mozes li mi dati primer nekog svog rezultata u matematici? Posto si odavno zavrsio studije! . Ja znam da ti mnogo robujes definicijama i teoremama i svakako jako puno stvari znas! Mozes li mi dati primer nekog svog rezultata u matematici? Posto si odavno zavrsio studije![Ovu poruku je menjao petarm dana 22.08.2008. u 18:25 GMT+1] [ petarm @ 22.08.2008. 17:22 ] @
Citat: Nedeljko: Ne vidim tu nigde  . . Pa i ne treba da ga vidis to je operator koji deluje na  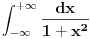 - necemo lutati po celoj matematici da bi mi ti pokazao da si formalno u pravu! Jer se ja s tim slazem! Ja hocu da ti kazem da ono sto sam ja napisao ce u praksi uvek raditi! - necemo lutati po celoj matematici da bi mi ti pokazao da si formalno u pravu! Jer se ja s tim slazem! Ja hocu da ti kazem da ono sto sam ja napisao ce u praksi uvek raditi!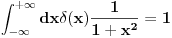 [ Nedeljko @ 22.08.2008. 19:05 ] @
Citat: petarm: Nije! Postoji li neki jači argument. Ako teoreme nisu, šta onda jeste? Ako je 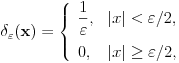 i i 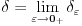 (u prostoru funkcija), onda je svakako (u prostoru funkcija), onda je svakako 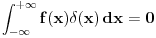 za ma koju funkciju za ma koju funkciju 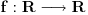 , jer inače ne bi bilo potrebe za teorijom distribucija. Ako je limes uzet u prostoru distribucija, onda je rezultat Dirakova distribucija. , jer inače ne bi bilo potrebe za teorijom distribucija. Ako je limes uzet u prostoru distribucija, onda je rezultat Dirakova distribucija.[ Nedeljko @ 22.08.2008. 19:41 ] @
Citat: petarm: Ja znam da ti mnogo robujes definicijama i teoremama i svakako jako puno stvari znas! Kao što rekoh, može se živeti i bez matematike. Može se zgrada sagraditi i na empirijskim znanjima i bez matematike, ali ako hoćeš da smanjiš eksperimentisanje i zasnuješ nešto na matematici, to ima smisla samo ako znaš da rezultat ima smisla, a matematički aparat ima smisla samo u kontekstu u kome je formulisan. Ti bi taj kontekst da zaobiđeš. Citat: petarm: Mozes li mi dati primer nekog svog rezultata u matematici? Teško da mogu ako ti formalizam nije jača strana. Bio sam logičar. Evo nečega što je 100% moje: http://www.elitesecurity.org/t320680-Paradoks-teoriji-skupova No, ovo nećeš razumeti, ali nema veze. Evo čime sam se bavio kao student (mada je sve bilo poznato ranije): 1. Na drugoj godini studija sam našao originalne dokaze osnovne teoreme algebre i Stirlingove formule za gama funkciju. 2. Takođe na drugoj godini studija dokazao sam da neprebrojivi zatvoreni podskupovi skupa 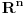 imaju moć kontinuuma (činjenica za koju nisam znao ranije). imaju moć kontinuuma (činjenica za koju nisam znao ranije).3. Kao student treće godine dao sam brz dokaz da se intuicionistička iskazna logika zaista razlikuje od klasične (kasnije sam video da je iste tablice našao Gedel). 4. Kao student četvrte godine sam dao originalan dokaz kompletnosti jedne aksiomatizacije implikativnog fragmenta klasične iskazne logike. 5. Takođe kao student četvrte godine sam našao algebru (zajedno sa svim potrebnim algoritmima) za računanje sa algebarskim brojevima u apsolutnoj tačnosti u opštem slučaju (uključujući i odlučivanje da li dve reprezentacije određuju isti broj). Ovo je nešto od onoga čega sam se setio. Kada budeš poslediplomac, možda budemo pričali o tome šta sam radio onda, ali se odavno ne bavim matematikom. [ Nedeljko @ 23.08.2008. 11:03 ] @
Ja mogu da razumem ljude koji kažu da im matematika nije potrebna, ali mi nisu jasni oni koji kažu da im su im bitni račun i rezultat, ali da im je potpuno svejedno da li je rezultat tačan. OK, ako im je bitan samo neki rezultat, ali ne i tačnost istog, do njega se može doći i bez računa - odvali se neka cifra i gotovo!
[ petarm @ 23.08.2008. 11:25 ] @
Svaka cast! Ipak covek mora nekad da radi nesto na intuiciju!
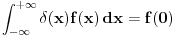 Kako bi po tebi mogao da se definise pojam integrala ovde ne bi li ovo bilo formalno dobro definisano! Ja sam iskreno razmisljao o tome da pocnem da ucim ozbiljno teoriju distribucija, ali naisao sam na neke probleme! Npr. ZAD Resiti stacionarnu Sredingerovu jednacinu za cesticu u potencijalu 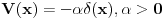 . Kakav je spektar energije? . Kakav je spektar energije?Ne znam kako bi se ovo moglo resiti primenom teorije distribucija?! I jos nesto u fizici se  cesto mora zbog nekih problema zapisati u obliku cesto mora zbog nekih problema zapisati u obliku 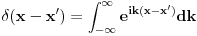 [ petarm @ 23.08.2008. 12:35 ] @
Sta je jos problem u fizici! Ti zapravo kad resis problem opservable koordinate
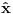 dobijes dobijes 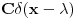 . A kako odredjujes . A kako odredjujes  ? Pa verovao ili ne u fizici se ovde primenjuje uslov normiranja gledajuci na ? Pa verovao ili ne u fizici se ovde primenjuje uslov normiranja gledajuci na  distribuciju kao na fju. distribuciju kao na fju.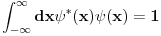 S tim sto ovde ne normiramo na jedinicu vec kazemo da normiramo na  -fju. -fju.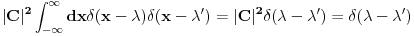 I onda biramo  realno i pozitivno tj. uzimamo realno i pozitivno tj. uzimamo 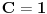 . . A u mnogim knjigama fizicari vole da kazu sto jos vise nervira matematicare  -fja je parna funkcija! -fja je parna funkcija!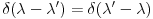 Dramski bi ovo zvucalo kao:"Matematicari fizicarima nikad nece moci da oproste  -fju". -fju".[ Nedeljko @ 23.08.2008. 19:25 ] @
Citat: petarm: ZAD Resiti stacionarnu Sredingerovu jednacinu za cesticu u potencijalu 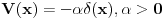 . Kakav je spektar energije? . Kakav je spektar energije?Hajde, daj matematičku formulaciju toga da se sad ne zezam i sa kvantnom mehanikom. [ petarm @ 25.08.2008. 13:52 ] @
[ petarm @ 25.08.2008. 14:26 ] @
Energija=konstanta!
[ petarm @ 25.08.2008. 14:32 ] @
Landau (dobitnik Nobelove nagrade za fiziku) u svom udzbeniku ''Nerelativisticka kvantna mehanika''-prevod s ruskog od strane Dragise Ivanovica:
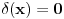 za za 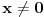 , , 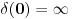 pri cemu je 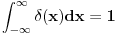 Kao granice integraljenja mogu se napisati ma koje druge, medju kojima se nalazi tacka  . Ako je . Ako je  neka funkcija, koja je kontinualna za neka funkcija, koja je kontinualna za  , onda je , onda je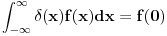 U opstijem slucaju ova formula se moze napisati ovako 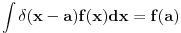 gde oblast integracije sadrzi tacku 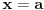 , a , a  je neprekidno za je neprekidno za 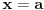 . .Takodje je ocigledno da je  -funkcija parna, tj. -funkcija parna, tj.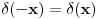 Najzad ako se napise 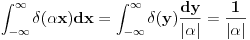 onda mozemo zakljuciti da je 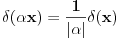 [ Nedeljko @ 26.08.2008. 11:00 ] @
[ petarm @ 26.08.2008. 12:10 ] @
[ Nedeljko @ 26.08.2008. 16:18 ] @
Moram priznati da nisam razumeo ideju. Moze li malo detaljnije?
[ petarm @ 26.08.2008. 17:08 ] @
Dovedem Sredingerovu jnu u tzv. Sturm - Liuvilov oblik:
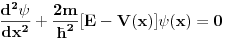 Posmatram dve oblasti! Oblast  mi je oblast za mi je oblast za 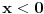 i oblast i oblast  mi je oblast za mi je oblast za 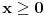 . Na granici izmedju oblasti mi vazi neprekidnost talasne fje . Na granici izmedju oblasti mi vazi neprekidnost talasne fje 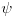 . Integraljenjem one jne iz mog prethodnog posta dobijas . Integraljenjem one jne iz mog prethodnog posta dobijas 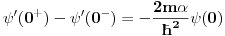 . Ovaj uslov i uslov neprekidnosti talasne fje . Ovaj uslov i uslov neprekidnosti talasne fje 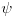 u fizici katkad zovemo i uslovi ''zasivanja''. u fizici katkad zovemo i uslovi ''zasivanja''. 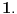 Oblast OblastSredingerova jna je 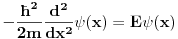 I slicno i za drugu oblast uz pomenute uslove! U problemu slobodne cestice 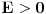 . Zasto ja ovde diskutujem slucaj . Zasto ja ovde diskutujem slucaj  ? Pa verovatno ti se opet nece svideti! ? Pa verovatno ti se opet nece svideti!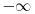 jer sam definisao da mi jer sam definisao da mi  -funkcija u nuli ima vrednost -funkcija u nuli ima vrednost  . . Nadam se da sam bio dovoljno detaljan?! [Ovu poruku je menjao petarm dana 26.08.2008. u 20:24 GMT+1] [Ovu poruku je menjao petarm dana 26.08.2008. u 20:24 GMT+1] [ Nedeljko @ 27.08.2008. 09:35 ] @
Da, ovo ocigledno nema resenje u teoriji distribucija, ali to ne znaci da ne postoji matematicki aparat u kome se, sa stanovista fizike, ovo ne moze raditi korektno. O tome cu malo kasnije.
[ Nedeljko @ 27.08.2008. 11:07 ] @
Mozes fizicki da posmatras stvari ovako: Potencijal je skoncentrisan u nekoj maloj okolini nule i integral mu je jedinica (ali je beskonacno diferencijabilna funkcija). Ona potrazi rezultat tvog fizickog problema kao limes kada je ta okolina beskonacno mala.
[ petarm @ 27.08.2008. 14:33 ] @
Ne vidim zasto bih to radio? Necu sebi da komplikujem zivot ako mi ovaj nacin radi i dobijam tacan rezultat! Da sve moze da se odradi preko teorije distribucija rekao bih OK. Ali ovako mislim da sve to matematicarsko "trazenje dlaka" nema smisla!
[ Nedeljko @ 28.08.2008. 08:45 ] @
Pa, upravo si sam dao odgovor:
Citat: petarm: Necu sebi da komplikujem zivot ako mi ovaj nacin radi i dobijam tacan rezultat! Sustina je u onom ako. Jer, ako znas da je rezultat tacan (sa stanovista tvoje primene), voleo bih da znam odakle to znas. Citat: petarm: Da sve moze da se odradi preko teorije distribucija rekao bih OK. Ne postoji nijedna "svemoguca" naucna teorija. To je kako kada bi rekao: "Da moze sve da se odradi u jednoj fizickoj teoriji, rekao bih OK. Ovako je fizika gubljenje vremena.". No, sve probleme ove vrste razresava nestandardna analiza. Mozes li mi reci kakvog fizickog smisla ima tackasti potencijal? Koliko mi je poznato, ako imas bilo koji izvor naelektrisanja, ceo prostor je ispunjen nekim neprekidnim potencijalom. [ petarm @ 28.08.2008. 12:22 ] @
Zato sto se ovi rezultati u fizici primenjuju jako mngo u raznim casopisima i jos se nije desilo da neki matematicar uradi istu stvar egzaktno i dobije razlicit rezultat! Ja znam da je tvoj najveci argument to da Lebegov integral "ne oseca" jednu tacku! To je tzv. skup Lebegove mere nula! Ali ja posmatram kao sto sam vec napisao na ovom delu foruma da je
 fja definisana na intervalu fja definisana na intervalu 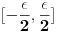 i da je maksimum ove fje i da je maksimum ove fje 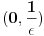 . I onda u granicnom slucaju posmatram . I onda u granicnom slucaju posmatram 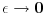 . A bilo koji rezultat u fizici se proverava i matematikom i eksperimentom! . A bilo koji rezultat u fizici se proverava i matematikom i eksperimentom! [ petarm @ 28.08.2008. 12:37 ] @
A vi matematicari ste destruktivni i trazite dlaku u svemu u tom smislu sto ti u celoj ovoj raspravi nisi dao nijedan primer gde meni Teorija distribucija moze koristiti kao fizicaru! A ja sam ti napisao nesto sto se zaista koristi u praksi i fizicara i inzenjera! I jos sam ti dao primer gde ne mozes koristiti Teoriju distribucija! Inace primer zadatka koji sam ti dao je iz beogradske zbirke zadataka iz kvantne mehanike od autora - Ivanovic, Buric. I moze se naci i u mnogim svetskim zbirkama! Preciznije receno prepisan je iz neke od njih! I potencijal moze biti prekidna fja. Evo ti primer beskonacno duboke potencijalne jame! Gde je potencijal na intervalu
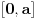 nula, a van tog intervala je nula, a van tog intervala je  [ Nedeljko @ 28.08.2008. 16:44 ] @
Citat: petarm: Zato sto se ovi rezultati u fizici primenjuju jako mngo u raznim casopisima i jos se nije desilo da neki matematicar uradi istu stvar egzaktno i dobije razlicit rezultat! Tu sam te čekao. Ako već znaš rezultat (iz časopisa), šta će ti onda račun? Onda jednostavno znaš rezultat iz nekog drugog izvora. Postoje tri slučaja: 1. Rezultat znaš. 2. Rezultat ne znaš, ali ti nije ni potreban. 3. Rezultat ne znaš i potreban ti je. U prva dva slučaja nema potrebe ni pribegavati računu, a u trećem je važno i da li je rezultat tačan. Citat: petarm: Ja znam da je tvoj najveci argument to da Lebegov integral "ne oseca" jednu tacku! To je tzv. skup Lebegove mere nula! Ne. Moj argument je da matematičke teoreme (od kojih je sačinjen bilo koji matematički aparat) važe pod uslovima koji su u njima navedeni. Van toga, matematički aparat je ravan gatanju. Citat: petarm: Ali ja posmatram kao sto sam vec napisao na ovom delu foruma da je  fja definisana na intervalu fja definisana na intervalu 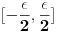 i da je maksimum ove fje i da je maksimum ove fje 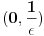 . I onda u granicnom slucaju posmatram . I onda u granicnom slucaju posmatram 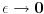 . .Ako si već izabrao  , onda ga ne možeš naknadno "menjati" raznim graničnim procesima (niti na drugi način). U ovom slučaju , onda ga ne možeš naknadno "menjati" raznim graničnim procesima (niti na drugi način). U ovom slučaju  zavisi od zavisi od 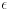 , pa bi ga bilo bolje označiti sa , pa bi ga bilo bolje označiti sa 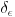 . No, šta god ja da napišem neće mnogo vredeti ako sam ne dođeš do zaključka gde grešiš. Zato, popravi ovo što si napisao da bih mogao da ti pomognem. Ne može . No, šta god ja da napišem neće mnogo vredeti ako sam ne dođeš do zaključka gde grešiš. Zato, popravi ovo što si napisao da bih mogao da ti pomognem. Ne može  biti oznaka za više različitih pojmova. biti oznaka za više različitih pojmova.[Ovu poruku je menjao Nedeljko dana 29.08.2008. u 09:36 GMT+1] [ petarm @ 28.08.2008. 17:14 ] @
Citat: Nedeljko:Tu sam te čekao. Ako već znaš rezultat (iz časopisa), šta će ti onda račun? Onda jednostavno znaš rezultat iz nekog drugog izvora. Postoje tri slučaja: 1. Rezultat znaš. 2. Rezultat ne znaš, ali ti nije ni potreban. 3. Rezultat ne znaš i potreban ti je. U prva dva slučaja nema potrebe ni pribegavati računu, a u trećem je važno i da li je rezultat tačan. Da tvoje rezonovanje je donekle OK. Kad je rec o matematici ono je skroz OK. Ali zasto kazem donekle? Zato sto ti u fizici imas istu ili slicnu matematiku koju primenjujes na razlicite probleme! To je fundamentalna razlika izmedju matematicara i fizicara?! Matematicari se odluce za oblast matematike koja ih zanima, njoj se posvete i u njoj postaju manje ili vise dobri. A da li znaju ostale oblasti matematike i koliko ih znaju to nije vazno pitanje! Za fizicara to ne stoji! On resava neki problem i priroda mu odredjuje koju ce matematiku da koristi! Moj profesor algebre na prvoj godini fizike rece jednom prilikom:"Fizicar je matematicar koji 100 puta resava jednu te istu diferencijalnu jnu samo jednom stavi da mu je nepoznata fja  , drugi put , drugi put  ..." Uzmi primer kvantne mehanike. Paul Adrien Maurice Dirac napisao je knjigu "Principi kvantne mehanike" u kojoj je za sve proracune koristio definiciju ..." Uzmi primer kvantne mehanike. Paul Adrien Maurice Dirac napisao je knjigu "Principi kvantne mehanike" u kojoj je za sve proracune koristio definiciju  fje koju sam ja koristio u ovoj diskusiji! John Von Neumann je rekao da se ne sme tako postupati za fje koju sam ja koristio u ovoj diskusiji! John Von Neumann je rekao da se ne sme tako postupati za  fjom i napisao je knjigu "Matematicki principi kvantne mehanike", ali je nazalost ili na srecu dobio sve iste rezultate kao Dirak. Da li je on time potvrdio Dirakovu teoriju? Ti ces reci ne! Ali ja kazem da jer postoje i eksperimenti tako da svaka teorija u fizici ima dve kontrole kvaliteta! fjom i napisao je knjigu "Matematicki principi kvantne mehanike", ali je nazalost ili na srecu dobio sve iste rezultate kao Dirak. Da li je on time potvrdio Dirakovu teoriju? Ti ces reci ne! Ali ja kazem da jer postoje i eksperimenti tako da svaka teorija u fizici ima dve kontrole kvaliteta!Citat: Nedeljko: Ako si već izabrao  , onda ga ne možeš naknadno "menjati" raznim graničnim procesima (niti na drugi način). U ovom slučaju , onda ga ne možeš naknadno "menjati" raznim graničnim procesima (niti na drugi način). U ovom slučaju  zavisi od zavisi od  , pa bi ga bilo bolje označiti sa , pa bi ga bilo bolje označiti sa 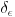 . No, šta god ja da napišem neće mnogo vredeti ako sam ne dođeš do zaključka gde grešiš. Zato, popravi ovo što si napisao da bih mogao da ti pomognem. Ne može . No, šta god ja da napišem neće mnogo vredeti ako sam ne dođeš do zaključka gde grešiš. Zato, popravi ovo što si napisao da bih mogao da ti pomognem. Ne može  biti oznaka za više različitih pojmova. biti oznaka za više različitih pojmova.Sa ovim cu se sloziti! 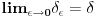 [ petarm @ 28.08.2008. 17:16 ] @
Mislim da imas neku tex gresku u prethodnoj poruci pa ispravi molim te da se lakse cita!
[ Nemanjich @ 28.08.2008. 21:08 ] @
Izvinite sto vam upadam u raspravu, ali cisto da dam paralelu sa time da fizika ima dve kontrole.Kao i pri resavanju odredjenih jednacina numerickim metodama, mi nikad ne cemo doci to bas tacnog resenja,vec cemo resenje znati uz odredjenu (ne)tacnost.
Pre oko pola godine bio sam na nekom predavanju o supersimetriji, na kome je predavac rekao da se ona poklapa rezultatski sa eksperimentom do neke 25 decimale i da ona predstavlja najtacniju teoriju za sada, koja se ipak ne slaze skroz sa eksperimentom.pretpostavljam da i ostale fiz. teorije imaju zadovoljavajucu tacnost, ali ipak sigurno nema teorije koja se u potpunosti slaze sa eksperimentom,zbog cega ipak mislim da bi matematika morala imati najvaniju ulogu sto se barem tacnosti tice u fizickim teorijama. [ petarm @ 28.08.2008. 21:23 ] @
Naravno! Ali ja bih rekao da sto je vece slaganje sa eksperimentom to je bolja teorija! A da bi odbacio neku teoriju potrebno je npr. da ne dobijes isti red velicine! Zapravo zna se koja teorija dozvoljava koliko odstupanje od eksperimenta!
[ Nedeljko @ 29.08.2008. 11:29 ] @
[ petarm @ 29.08.2008. 11:48 ] @
Pretpostavicu da mi u gornjem slucaju izmena limita i integrala nece uticati na rezultat! Jos jednom Nedeljko ti kazem da je meni matematika potrebna da bih dosao do odredjenog rezultata! Ja se slazem da sve ovo sa
 funkcijom (namerno kazem funkcijom) nije skroz korektno! Al daj mi primer kada cu dobiti razlicit rezultat koristeci teoriju distribucija i ovo! Iskonstruisi kontraprimer i ubedices me! funkcijom (namerno kazem funkcijom) nije skroz korektno! Al daj mi primer kada cu dobiti razlicit rezultat koristeci teoriju distribucija i ovo! Iskonstruisi kontraprimer i ubedices me![ petarm @ 30.08.2008. 14:22 ] @
Znas da budem iskren meni nije jasno zasto to radi? Ja znam da taj limes zapravo ne postoji?! U takvim situacijama mislim da bi se morala naci brzo situacija gde ce to da pukne. Ali ocigledno nije tako!
[ petarm @ 01.11.2008. 16:38 ] @
Evo jedan lep tekst koji delom ilustruje ono sto sam ja rekao! Mi na fizici imamo vezbe i pre vezbi ulazne kolokvijume na kojima se lepo nauci kako se radi vezba. Ali onda naidjemo na vezbe i vidimo da se u praksi to radi malo drugacije...
[ petarm @ 03.02.2009. 13:40 ] @
Citat: Nedeljko: 1. Na drugoj godini studija sam našao originalne dokaze osnovne teoreme algebre i Stirlingove formule za gama funkciju. 2. Takođe na drugoj godini studija dokazao sam da neprebrojivi zatvoreni podskupovi skupa imaju moć kontinuuma (činjenica za koju nisam znao ranije). 3. Kao student treće godine dao sam brz dokaz da se intuicionistička iskazna logika zaista razlikuje od klasične (kasnije sam video da je iste tablice našao Gedel). 4. Kao student četvrte godine sam dao originalan dokaz kompletnosti jedne aksiomatizacije implikativnog fragmenta klasične iskazne logike. 5. Takođe kao student četvrte godine sam našao algebru (zajedno sa svim potrebnim algoritmima) za računanje sa algebarskim brojevima u apsolutnoj tačnosti u opštem slučaju (uključujući i odlučivanje da li dve reprezentacije određuju isti broj). Ako se jos secas zanima me ovaj originalni dokaz FTA i Stirlingove formule za 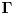 -fju. -fju. [ Nedeljko @ 04.02.2009. 11:02 ] @
Secam se svega, ali sam ovih dana u stiskavcu sa vremenom, pa mozda uradim za 10-tak dana.
[ petarm @ 04.02.2009. 14:17 ] @
OK odlicno
[ Nedeljko @ 11.02.2011. 23:02 ] @
[ petarm @ 12.02.2011. 00:20 ] @
Citat: Nedeljko: Da, ovo ocigledno nema resenje u teoriji distribucija, ali to ne znaci da ne postoji matematicki aparat u kome se, sa stanovista fizike, ovo ne moze raditi korektno. O tome cu malo kasnije. Ovo si napisao na drugoj strani na ovom forumu! [ Nedeljko @ 12.02.2011. 08:39 ] @
Pa šta. Obzirom da te dokazi ne zanimaju, svako rešenje je dobro. Recimo, evo još jednog - 42.
[ petarm @ 12.02.2011. 10:42 ] @
Sta mislis o Svetozaru Kurepi i njegovim knjigama Matematicka analiza 1, Matematicka analiza 2, 3 i 4?
[ Nedeljko @ 12.02.2011. 11:45 ] @
Nisam ih čitao, ali što se tiče analize 1, Milosav Marijanović je napisao sjajan udžbenik.
[ petarm @ 12.02.2011. 13:39 ] @
Citat: Nedeljko: Pa šta. Obzirom da te dokazi ne zanimaju, svako rešenje je dobro. Recimo, evo još jednog - 42. Zanima me postupak. Pogotovo kako se moze resiti pomocu teorije distribucija nesto sto se ne moze resiti pomocu teorije distribucija. Spomenuo sam ove knjige od Svetozara Kurepe jer u 3. knjizi Svetozar Kurepa koristi 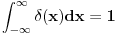 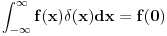 [ Nedeljko @ 12.02.2011. 15:32 ] @
Nije nikakav problem pisati
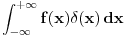 kao alternativnu oznaku za kao alternativnu oznaku za 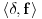 ako se zna šta se radi. ako se zna šta se radi.Opšte rešenje one jednačine u teoriji distribucija je jednoparametarsko, a ne dvoparametarsko, kako bi se dobilo u nestandardnoj analizi, tako da ne nalazim da je to podesna teorija za probleme u kojima se ta jednačina pojavljuje. Što se postupka tiče, ako te dokazi ne zanimaju, mogu ja i da skratim postupak i da predložim metod po kome je rešenje svakog problema 42. [ kandorus @ 11.04.2011. 14:21 ] @
Znate kad ćete se vi uskladiti? Nikad!
Fizičari polaze od eksperimenta a matematičari od definicija. Kvantna mehanika je u suštini "naštimavanje" formula da se poklope sa rezultatima eksperimenata. Sa druge strane ne možete "naštimavati" stvarnost da se poklopi sa definicijamam (to bi bilo moguće samo u ograničenim sredinama, na primer u veštačkim sistemima). Rezultat Lebegovog integrala za izolovanu tačku jednak je nuli. Ali u prirodi postoje pojave koje nisu obuhvaćene definicijom Lebegovog integrala. Tada nam ostaje (1) da odbacimo stvarnost, što je nemoguće, ili (2) da dodefinišemo matematički aparat kojim opisujemo posmatranu pojavu. Reklo bi se da je ovo pod (2) jedini ispravan postupak. Čovek uzme papir i olovku, isproba neke formule i ako se potrefe sa eksperimentalnim rezultatima dobije Nobelovu nagradu. Ako se izračunati rezultati ne poklope sa ekperimentalnim čovek ostaje anonimus koji je eventualno poznat po prepucavanju sa onima koji su dobili Nobelovu nagradu. Ali niko neće, zbog izračunavanja dobijenih nekom formulom, naštimavati rezultate eksperimenata. Takav se nadje na listi šarlatana ili prevaranata. Jedino što može da se "naštimava" to su uslovi eksperimenta i da se tim putem dodje do odredjenog rezultata. Tu matematika može da ima doprinos ali to je drugo pitanje. Zaista, inženjer kad tamo konstruiše mostove koristi približne formule jer su besmislene "tačne" formule kojima se dobija "u mikrogram" koliko treba betona. Zato što, dok kašika krana prenese umešan beton iz mešalice do mesta ugradnje okolo se raspe na milione puta više betona nego što je onih "u dlaku tačno" izračunatih mikrograma. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|