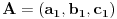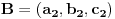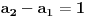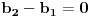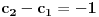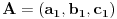
neka je i
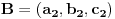
iskoristi uslove AB=AC=BC. iz uslova da tacke A i B pripadaju pravcu , mozes dobiti sljedece jednacine.



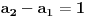
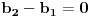
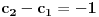
odatle se moze nesto iskombinovati.

Dalje napravis sistem od 2 jednacine sa 2 nepoznata parametra a i b:

d(AC)=d(BC)
d(AC)=d(AB)

koje kada se kvadriraju glase:

(a+1-1)^2 + (2-4)^2 + (-a+3-1)^2 = (b+1-1)^2 + (2-4)^2 + (-b+3-1)^2
(a+1-1)^2 + (2-4)^2 + (-a+3-1)^2 = (a+1-b-1)^2 + (2-2)^2 + (-a+3+b-3)^2


odnosno:

a^2 + 4 + a^2 - 4*a + 4 = b^2 + 4 + b^2 - 4*b + 4
a^2 + 4 + a^2 - 4*a + 4 = a^2 -2a*b + b^2 + 0 + a^2 -2a*b + b^2

odnosno:

a^2 - 2*a = b^2 - 2*b
4 - 2*a =b^2 - 2*a*b

odnosno:

(a-b)*(a+b-2)=0
4 - 2*a =b^2 - 2*a*b

a=b ne daje trugao (poklapale bi se tacke A i B), vec (a+b-2)=0 odnosno a=2-b sto zamenom u drugu jedanacinu daje:

4-4+2*b = b^2 - 4*b + 2*b^2

odnosno:
3*b^2-6*b=0

b=0 ili b=2
a=2 ili a=0

za (b=0, a=2) imamo A(3,2,1) a B(1,2,3)
za (b=2, a=0) imamo A(1,2,3) a B(3,2,1) sto je isto resenje geometrijski.

Provera: d(AB)=d(AC)=d(BC) = koren(8)

_{[Ovu poruku je menjao miki069 dana 26.08.2008. u 00:26 GMT+1]}

neka neko pomogne
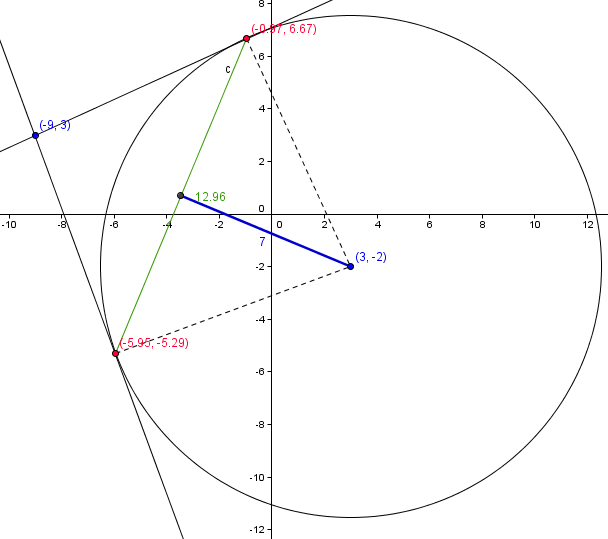
Iz tacke (-9, 3) povucene su tangente na kruznicu x2+y2-6x+4y-78 = 0. Izracunati
udaljenost sredista kruznice od tetive koja spaja diralista tih tangenata.

pocela nest:
(x-3)2+(y+2)2=91 p=-3 q=2 r2=91

nasla sam pravu i sta dALJE:(TETIVU)

na osnovu datih podataka mozes naci dodirne tacke tangenti i kruznice. te tacke su krajevi duzi (tetive). posto znas krajnje tacke, mozes izracunati i duzinu te tetive, a i njenu polovinu. onda po pitagorinoj t. nadjes rastojanje od sredista kruznice do sredista tetive.

Vriskice, bez skice ide mnogo teze.
Evo ti skica, postupak rada si vec dobila a rastijanje je 7.