[ h4su @ 29.08.2008. 12:14 ] @
Kao sto stoji u naslovu,zasto kako,kako svatamo pojam beskonacnosti ? |
|
[ h4su @ 29.08.2008. 12:14 ] @
[ petarm @ 29.08.2008. 12:17 ] @
Ne!
[ Bojan Basic @ 29.08.2008. 13:15 ] @
Jeste jednako.
[ cedomir @ 29.08.2008. 13:19 ] @
Po matematici nije, po fizici jeste.
[ petarm @ 29.08.2008. 13:23 ] @
Koliko je meni poznato sa jednom tackicom bi trebalo da se oznaci ako hoces da kazes da ti se cifre ponavljaju do beskonacnosti. Ovo sto si ti napisao moze da bude broj 0,99999991111111111112222222222233333333333... sto nije 1.
[ igorpet @ 29.08.2008. 13:54 ] @
Citat: da li je 0.9999999... jednako 1 ? Ako rezultat zaokruzujemo - onda moze biti 1, a ako nam treba veca preciznost onda nije 1. I da je 0.9999999... jednako 1 onda bi ga pisali 1 a ne 0.9999999... U principu 0.9999999... ne moze biti 1 osim ako nam ne treba neka konkretna tacnost. I ove tri tackice na kraju oznacavaju da se 9-ke ponavljaju do beskonacnosti, i ne mogu zadnje cifre biti nesto drugo sem 9-ke. Valjda nema neke greske u mojoj logici [ h4su @ 29.08.2008. 14:04 ] @
Heh i ja sam na prvu rekao wtf kako jedanko al jeste.Naletim na ovu stranicu i pocnem citati komentare heh svasta se moze vidjeti.Evo vam link:
http://polymathematics.typepad...h/2006/06/no_im_sorry_it_.html. Ta beskonacnost je cudo jedno,na prvu se fakat cini da je 0.99999... blizu 1 ali da nije 1, mada netreba razmisljati na taj nacin nego cisto kao da je 0.9999... samo drugi nacin zapisa broja 1. Koliko je meni poznato Petre uvijek se sa tri tacke oznacavalo. [ Bojan Basic @ 29.08.2008. 14:05 ] @
Citat: petarm: Koliko je meni poznato sa jednom tackicom bi trebalo da se oznaci ako hoces da kazes da ti se cifre ponavljaju do beskonacnosti. Što je jedan od načina zapisa, ali ne znam otkud ti ideja da je i jedini. Ako je jasno na koji način se decimale nastavljaju, nema nikakvog problema staviti tri tačkice (a ako ti nije jasno, možeš zamoliti autora teoreme da objasni šta je podrazumevao pod oznakom koju je upotrebio; kladim se da ćeš se iznenaditi Citat: Tvrdiš, dakle, da su ovaj broj i broj  dva različita realna broja. Dobro, u tom slučaju je i njihova razlika realan broj. Možeš li mi reći koliko iznosi ta razlika? dva različita realna broja. Dobro, u tom slučaju je i njihova razlika realan broj. Možeš li mi reći koliko iznosi ta razlika? [ Emil Ranc @ 29.08.2008. 14:40 ] @
[ petarm @ 29.08.2008. 14:43 ] @
Citat: Bojan BasicŠto je jedan od načina zapisa, ali ne znam otkud ti ideja da je i jedini. Ako je jasno na koji način se decimale nastavljaju, nema nikakvog problema staviti tri tačkice (a ako ti nije jasno, možeš zamoliti autora teoreme da objasni šta je podrazumevao pod oznakom koju je upotrebio; kladim se da ćeš se iznenaditi Ako ti neko napise niz 1,1,1,1,1,... i pita te da li je sledeci clan niza jednak 1 sta ces mu reci? Mozda je umesto ne bio bolji odgovor ne znam ili mozda, ali moj odgovor je svakako bolji od jeste jer ne mora bit! [ igorpet @ 29.08.2008. 15:04 ] @
Citat: Bojan Basic: Tvrdiš, dakle, da su ovaj broj i broj  dva različita realna broja. Dobro, u tom slučaju je i njihova razlika realan broj. Možeš li mi reći koliko iznosi ta razlika? dva različita realna broja. Dobro, u tom slučaju je i njihova razlika realan broj. Možeš li mi reći koliko iznosi ta razlika? 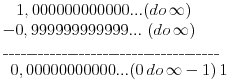 [ Bojan Basic @ 29.08.2008. 15:16 ] @
Citat: petarm: Ako ti neko napise niz 1,1,1,1,1,... i pita te da li je sledeci clan niza jednak 1 sta ces mu reci? Mozda je umesto ne bio bolji odgovor ne znam ili mozda, ali moj odgovor je svakako bolji od jeste jer ne mora bit!:) A iznenadio sam se moram biti iskren!:) Ako je neko računao prvih pet članova niza pa dobio pet jedinica, naravno da to ne znači kako će i šesti član biti jedinica; no, to nema veze s ovim. Ako neko misli na konkretan niz (tj. zna mu sve članove) pa hoće meni da objasni na koji niz misli, može da napiše: „to je niz kome su svi članovi jednaki  “, ili „ “, ili „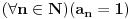 “, ili „ “, ili „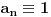 “, a svakako ne bih bio u nedoumici ni da napiše „ “, a svakako ne bih bio u nedoumici ni da napiše „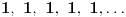 “. Ako ja tebi kažem: „Pričam o nizu “. Ako ja tebi kažem: „Pričam o nizu 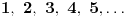 “ i pri tom odajem utisak kao da ti objašnjavam tačno određeni niz čije ćeš članove dalje i sam shvatiti na osnovu ovih nekoliko — šta misliš, koji niz ti pominjem? “ i pri tom odajem utisak kao da ti objašnjavam tačno određeni niz čije ćeš članove dalje i sam shvatiti na osnovu ovih nekoliko — šta misliš, koji niz ti pominjem?[ h4su @ 29.08.2008. 19:23 ] @
To mu ga dodje isto kao i odrediti vjerovatnocu da izabrani broj iz skupa prirodnih brojeva jednak 542.Iako je to moguce vjerovatnoca je nula,jel tako? Mislim nema tu neke kontradikcije sto se tice same definicije vjerovatnoce u postavci problema ?
[ Nedeljko @ 29.08.2008. 20:07 ] @
[ Daniel011 @ 31.08.2008. 16:24 ] @
Diferencijal se definiše kao
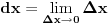 . Shvatamo ga kao beskonačno malu veličinu, ali koja ipak nije nula. Zbog čega ne bi razlika brojeva 1 i 0.999... takođe mogla biti beskonačno mala veličina koja nije nula (kao što je igorpet i napisao)? . Shvatamo ga kao beskonačno malu veličinu, ali koja ipak nije nula. Zbog čega ne bi razlika brojeva 1 i 0.999... takođe mogla biti beskonačno mala veličina koja nije nula (kao što je igorpet i napisao)?[ Bojan Basic @ 31.08.2008. 20:48 ] @
Zato što je skup realnih brojeva zatvoren u odnosu na operaciju oduzimanja, tj. razlika ma koja dva realna broja mora opet biti realan broj (a nijedan realan broj ne odgovara opisu „beskonačna mala veličina koja nije nula“).
[ Nedeljko @ 01.09.2008. 08:12 ] @
Citat: Ovo nije tacno, barem u klasicnoj analizi, jer tu nema beskonacno malih i beskonacno velikih velicina. [ petarm @ 02.09.2008. 15:25 ] @
Mozda bi trebalo da malo detaljnije prokomentarises ovo bar u klasicnoj analizi!
[ Nedeljko @ 02.09.2008. 16:34 ] @
Izračunaj citirani limes. Šta će nam dodatna oznaka za nulu, kad već imamo jednu?
[ Cabo @ 12.09.2008. 20:20 ] @
[ dkoncar @ 12.09.2008. 21:36 ] @
Odgovor je veoma prost:
ako je x=0,9999999... onda je 10x=9,9999999... dalje je: 10x-x=9,9999999... - 0,9999999... 9x=9 pa je x=1 Znači: 0,9999999...=1 ŠTD (Što je Trebalo Dokazati). Pozdrav! [ peddja_stankovic @ 15.09.2008. 15:43 ] @
prema kantorovom principu umetnutih odsecaka 0.9999999999.... = 1
[ axx420 @ 15.09.2008. 20:04 ] @
Moram priznati da me ništa od navedenog nije ubedilo da je 0.9999999...=1 dok nisam pročitao ovo:
1/3=0.3333333... 2/3=0.6666666... + ----------------- 3/3=0.9999999... Pozdrav. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|