[ petarm @ 30.08.2008. 14:15 ] @
ZAD
Hamiltonijan cestice mase koja se krece u dvodimenzionoj oblasti

ima oblik



gde je konstanta. Ako se cestica nalazi u stanju



gde je , a konstanta koju treba odrediti, izracunati:

a) verovatnocu da se prilikom merenja energije cestice dobije osnovna energija;

b) srednje vrednosti operatora .

res: Dobio sam da mi se problem raspada na dva problema! Jedan je LHO po , a drugi beskonacno duboka potencijalna jama po . Za energiju osnovnog stanja dobijam:



a odgovara joj osnovno stanje

Problem mi je da izracunam ovo pod a) i b) mada pretpostavljam da je vrlo jednostavno. Pod a) treba da se dobije . A pod b) .

[Ovu poruku je menjao petarm dana 30.08.2008. u 23:00 GMT+1]
[ tomkeus @ 30.08.2008. 18:24 ] @
Da li su problem integrali ili kako da dobiješ rešenje?
[ petarm @ 30.08.2008. 18:54 ] @
Integrali! Cini mi se da gutam konstante!

[Ovu poruku je menjao petarm dana 30.08.2008. u 20:21 GMT+1]
[ tomkeus @ 30.08.2008. 19:49 ] @
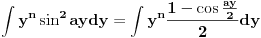
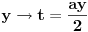
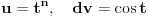
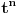
Integrali su stvarno jednostavni. Prilikom integracije po y imaćeš integrale tipa koje lako rešavaš smenom i parcijalnom integracijom uzimanjem da je i ponovnom parcijalnom integracijom sve dok se ne izgubi član i ostane samo trigonometrijski član. Prilikom integracije po x imaćeš integrale tipa

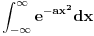
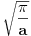
1. što je Gausov integral i njegova vrednost je . On je dat u tablicama, a ako ti se baš računa pokazao sam kako u nekoj tvojoj temi na podforumu za matematiku.

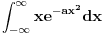
2., koji je jednak nuli jer je u pitanju integral neparne funkcije na simetričnom intervalu, i

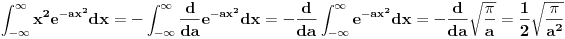
3. pri čemu je iskorišćena vrednost Gausovog integrala.

P.S. Za konstante ne mogu da ti pomognem.
[ petarm @ 30.08.2008. 22:31 ] @
Moj prvi problem nastaje kada pokusam da normiram fju tj. kada odredjujem konstantu .



gde mi predstavljaju zbir od vise clanova od kojih je npr. prvi oblika

A integral

divergira!

[ tomkeus @ 30.08.2008. 23:45 ] @
Integral po y ide od 0 do l.
[ petarm @ 30.08.2008. 23:58 ] @
Glupa greska! Skroz sam zaboravio na to. Ustedeo si mi dosta vremena! Hvala!
[ petarm @ 31.08.2008. 00:13 ] @
Citat:
tomkeus: 
3. pri čemu je iskorišćena vrednost Gausovog integrala.



Samo mala ispravka! Ovde se dobija





[ petarm @ 31.08.2008. 00:28 ] @
Dobija se

[ bobanex @ 31.08.2008. 09:51 ] @
Tomkeus, kvadrat sinusa se izrazava preko kosinusa dvostrukog ugla.
[ petarm @ 31.08.2008. 15:55 ] @
Dobro jasno je sta je hteo reci!

[ petarm @ 06.09.2008. 13:30 ] @
ZAD
Izracunati proizvod disperzija koordinate i impulsa u -tom stanju L.H.O.
a) pokazati na osnovu rezultata da je osnovno stanje L.H.O. stanje s minimalnim proizvodom disperzije.
b) zasto su ovi rezultati razliciti od nule iako je rec o sv. stanjima?

RES:
Dobijem:




i dobije se



b) Mislim da je odgovor jednostavan. Prostonu to su sv. stanja Hamiltonijana, a i ne komutiraju s njim! A sta treba uraditi pod a) Kako najlakse to uraditi?