[ R_O_L_E @ 02.09.2008. 14:04 ] @
| Molim vas za malu pomoć kod ovog integrala... Gubim se u pustim parcijalnim integracijama ali nikako do rješenja... ∫▒(arcsin√x)/√(1-x) dx Hvala! |
|
[ R_O_L_E @ 02.09.2008. 14:04 ] @
[ igorpet @ 02.09.2008. 14:37 ] @
Valjda je sve dobro. Nabrzaka sam, pa nisam stigo da proverim.
I kod mene samo jedna smena i jedna parcijalna integracija 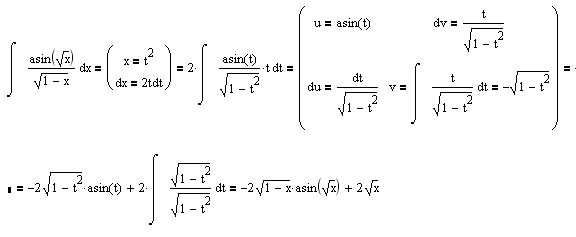 [ R_O_L_E @ 02.09.2008. 16:21 ] @
Hvala najljepša! E to sam i ja uradio između svih ostalih raznih tehnika...:) Samo sam bio u zabuni (i još sam...) u svezi s integralom ∫▒t/√(1-t^2 ) dt... Ja sam našao u jednoj proširenoj tablici integrala da je rješenje -√(1-t^2 ). Ali moram priznati da nemogu nikako nekom tehnikom integriranja doći do toga iako rješavam dobru većinu integrala bez problema... Valjda od puno stabala ne vidim šumu...:) Pa ako neko može uskočiti bio bi zahvalan. E i kako ubaciti tu u odgovor ove slike kad se pišu izrazi da ipak izgleda jasno?
Hvala još jednom na odgovoru i pohvala velika svima koji pomažu. I ja se rado pridružujem. [ igorpet @ 02.09.2008. 16:47 ] @
Citat: R_O_L_E: ... Samo sam bio u zabuni (i još sam...) u svezi s integralom ∫▒t/√(1-t^2 ) dt... Ja sam našao u jednoj proširenoj tablici integrala da je rješenje -√(1-t^2 ). Ali moram priznati da nemogu nikako nekom tehnikom integriranja doći do toga iako rješavam dobru većinu integrala bez problema... ... R_O_L_E brzo reci da se zezas da neznas da resis ovaj integral iz parcijalne integracije, pa to ti je ... vrlo jednostavno ... 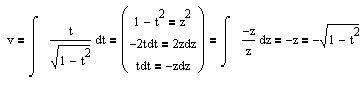 [ R_O_L_E @ 02.09.2008. 17:08 ] @
Ma zezam se, zezam se...
[ igorpet @ 02.09.2008. 17:28 ] @
Citat: R_O_L_E: Ma zezam se, zezam se... Ma odmah sam znao da se zezas. Eto vidis da si znao da uradis [ R_O_L_E @ 02.09.2008. 17:44 ] @
E opet jedno pitanje... Što napraviti kod integriranja racionalnih funkcija kad je stupanj brojnika manji od stupnja nazivnika? točnije u integralu ∫▒xdx/(x^3-3x+2)... Kako točno podijeliti polinome?
[ igorpet @ 02.09.2008. 18:10 ] @
Pa u tom slucaju, ako ne moze direktno da se primeni smena, najbolje je racionalisati funkciju (ili ako i to neznas onda pitati, kao sada
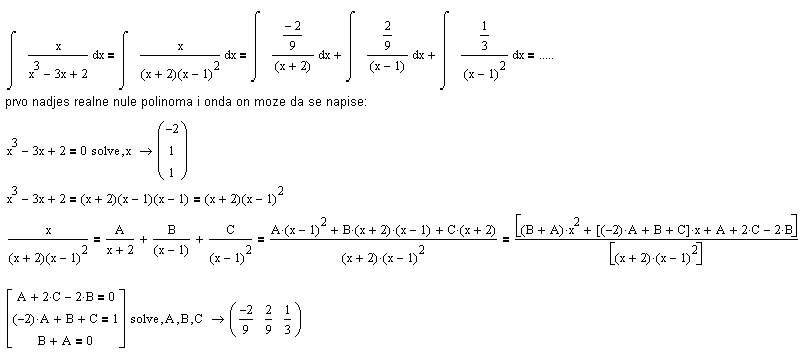 [ Kolins Balaban @ 02.09.2008. 18:19 ] @
pokusas rastaviti na parcijalne razlomke ;)
[ igorpet @ 02.09.2008. 19:31 ] @
Citat: igorpet: ... najbolje je racionalisati funkciju ... Ha, ha, ha, al sam ti dao dobar savet ... nego dobro je sto taj savet nisam primenio na zadatak I kao sto rece Kolins Balaban ipak treba rastaviti na parcijalne razlomke. Pogresno sam se izrazio jer sam hteo da kazem: najbolje je da ovu racionalnu funkciju ... ha,ha,ha i nemam pojma sto sam to pokusao da skratim tekst (valjda me mrzelo da kucam) [ R_O_L_E @ 02.09.2008. 19:39 ] @
Ma da to je jasna stvar ali možda je malo preglupo no muči me rješit taj nazivnik x(na 3)-3x+2...
(xna3-3x+2) [ R_O_L_E @ 02.09.2008. 19:40 ] @
tamo nije smile nego (xna3-3x+2) : (x-1)... sorry
[ R_O_L_E @ 02.09.2008. 19:43 ] @
[ igorpet @ 02.09.2008. 20:32 ] @
Citat: R_O_L_E: Ma da to je jasna stvar ali možda je malo preglupo no muči me rješit taj nazivnik x(na 3)-3x+2 ... ali nikako mi nije jasan taj (x-1)??? Pa kod ovih zadataka (polinoma) probas da nadjes jednu nulu probom. Obicno treba da probas neku od ovih vrednosti 1,-1,2,-2,3,-3 i kada "ubodes" odgovarajucu vrednost (nulu) onda podelis polinom i smanjis ga za jedan stepen. Ako bas ne moze probom da se nadje realna nula, onda za polinome treceg stepena, primenis Kardanove formule (imas detalje na http://www.elitesecurity.org/t327275-Problem-sa-jednim-integralom ) i tako nadjes realne nule ili barem jednu i onda podelis polinom i smanjis mu stepen. Valjda sam uspeo da ti razjasnim postupak, ako sam dobro razumeo pitanje i sta te buni. [ R_O_L_E @ 02.09.2008. 20:49 ] @
Jesi jesi. Velika hvala. To mi nije bilo jasno jer sam zaboravio kako te polinome trećeg stupnja smanjiti... Nisam bio siguran jeli se napamet proba s 1 ili 2 ili treba nešto drugo prije napraviti. Sad je jasno.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|