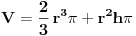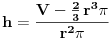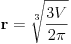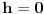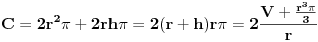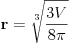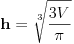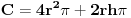[ different @ 03.09.2008. 08:44 ] @
| 1.silos ima oblik cilindra koji se zavrsava sa plusferom, izgradnja 1 kvadratnog metra spoljnje površine sfernog dijela je dva puta skuplja nego izgradnja 1 kv.metra spoljne povrsine cilindricnog dijela. potrebno je odrediti dimnzije silosa date zapremine V, tako da troskovi nj.izgradnje budu najmanje moguci. POkusao sam uraditi navedeni zadatak,al ne mogu nikako da uspostavim korelaciju izmedju cijene i povrsine uz datu V... |