najprije lijep ti pozdrav

Recimo da zelis mjeriti polozaj kvantne cestice.
Kao sto i sam znas, ta cestica prije samog mjerenja moze biti bilo gdje, tj nema tocno odredjen polozaj i opisana je valnom funkcijom koja je rasprostranjena po prostor-vremenu na nacin da kvadrat njenog modula daje vjerojatnost nalazenja cestice u tocki r u trenutku t.
Graf tipicne valne funkcije neke cestice prije mjerenja dakle ima bregove i doline i rasiren je po prostoru (tj nije "kolabiran")

Nakon izvrsenog mjerenja, dobijemo rezultat npr da je cestica u polozaju r1.

E sad ako izvrsimo drugo mjerenje ODMAH! (naglasak na odmah, tj vrlo brzo) nakon prvog, ocekujemo da cemo dobiti isti rezultat (jer inace ne bismo mogli provjeriti tocnost naseg prvog mjerenja).
No ako znamo da cemo dobiti isti rezultat, tj isti polozaj r1, to moze znaciti samo jedno - valna funkija (odnosno njen graf) vise nije (neposredno pred drugo mjerenje) rasprostranjena po prostoru, nego je "kolabirala" iznad tocke r1 (nesto poput delta "funkcije"), jer je "sigurno" da cemo u drugom mjerenju (obavljenom odmah nakon prvog) cesticu naci u r1.
E ta "sigurnost" je opisana dakle kolabiranom valnom funkcijom (koja je nula svuda osim u tocki r1) a ne valnom funkcijom rasprostranjenom po prostoru.

Ovdje sam naglasio vaznost drugog mjerenja "odmah" nakon prvog.
Jer ako to ne obavimo odmah, nego nakon nekog vremna, valna funkcija ce se naravno opet rasiriti prema schroedingerovoj jednadzbi i necemo znati gdje je cestica, tj ona ce opet biti opisana uobicajenom ("nekolabiranom") valnom funkcijom.

Dakle, svako mjerenje uzrokuje kolabiranje valne funkcije u trenutku odmah nakon mjerenja. Nakon nesto duzeg vremena, funkcija se vraca u uobicajeni oblik.

Odakle izraz "kolabirati"?!

I mozes li povezati ovu pricu sa svojstvenim vrednostima?

Pozdrav i tebi!

Pa kolabirati - u smislu "urusiti se" - da sad ne crtam, zamisli graf neke obicne funkcije sa R u R u kartezijevom sustavu koji se rasprostire duz cijele x-osi i iznad nje (sto je slucaj npr prije prvog mjerenja), i onda zamisli kako se taj graf (odmah nakon prvog mjerenja) sazima oko tocke r1 na x osi tako da postaje nula svuda a u toj tocki ima neki maximum (kao sto rekoh, slicno delta "funkciji").
I onda se opet nakon nekog vremena graf rasprostire po cijelom prostoru, i opet cim ucinimo mjerenje graf kolabira, sazme se na trenutak oko izmjerene velicine... pa se opet nakon nekog vremena "rasiri" u uobicajeni oblik, itd..
Mislim da je izraz zgodno odabran.

Sto se tice povezivanja sa pricom o svojstvenim vrijednostima - ne znam zasto bi trebalo povezivati s ikakvom drugom pricom. Ovo objasnjenje je po meni dovoljno da se objasni sto znaci kolaps valne funkcije. Eventualno se moze povezati u uobicajenom smislu koji sigurno znas - da se rezultat mjerenja (tj r1 u nasem slucaju) mora nalaziti u spektru odgovarajuce observable. Ali ja sam jos uvijek tek na vratima kvantnog svijeta, pa ovo uzmi s rezervom, tj mozda postoji i neka dublja povezanost.

Ne nego mislio sam u smislu kolaps - kolapsirati, a ne kolabirati! Ja sam cuo da ne prihvatuju bas svi ovu pricu o kolapsu?! U svakom slucaju prica ima smisla. Ja sam to zamisljao kao imas neku fju


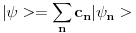Ti razvijas neko ''preparirano'' stanje po svojstvenim fjama opservable koju meris i sistem ti predje u neko stanje 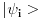pa u tom smislu urusenje. Bez price o talasnim paketima! Naravno koristio mi je tvoj odgovor puno! Hvala ti!

Ne, ispravno je kolaps-kolabirati, kao i aplauz-aplaudirati, eksplozija-eksplodirati, aluzija-aludirati, depresija-deprimirati itd.

Ok. Moja greska onda! Hvala! Nisam znao ovo!